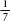Alex’s Adventures in Numberland (24 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

The ancient civilizations realized that the ratio of a circle’s circumference to its diameter was always the same no matter how big or small you made the circle. (The circumference is the distance around a circle, and the diameter is the distance across it.) The ratio is known as pi, or p, and it works out as just over three. So, if you take the diameter of a circle and curve it around the circumference, you will find that it fits just over three times.
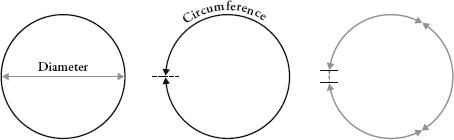
Even though pi is a simple ratio between the basic properties of a circle, the task of finding its exact value has proved to be far from simple. This elusiveness has made pi an object of fascination for thousands of years. It is the only number that is both the name of a song by Kate Bush and a fragrance by Givenchy, whose PR department sent me the following text:
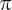 – PI
– PI
BEYOND INFINITY
Four thousand years have passed and the mystery remains.
Although every schoolchild studies, the familiar symbol still manages to hide an abyss of great complexity.
Why choose to symbolise the eternal masculine?
It’s a matter of signs and directions. If is the story of the long struggle to achieve the unattainable, it is also a portrait of the fabled conqueror in search of knowledge.
Pi speaks of men, of all men, of their scientific genius, their taste for adventure, their willingness to act, and of their passions to the extreme.
The earliest approximations for pi came from the Babylonians, who used a value of 3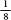 , and the Egyptians, who used 4(
, and the Egyptians, who used 4(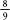 , which translate, respectively, into decimals as 3.125 and 3.160. A line in the Bible reveals a situation in which pi is taken as 3: ‘Also he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about’ (I Kings 7:23).
, which translate, respectively, into decimals as 3.125 and 3.160. A line in the Bible reveals a situation in which pi is taken as 3: ‘Also he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about’ (I Kings 7:23).
If the shape of the sea is a circle with a circumference of 30 cubits and a diameter of 10, then pi is , or 3. Many excuses have been given for the Bible’s inaccurate value, such as the claim that the sea was in a circular vessel with a thick rim. In this case the quoted 10-cubit diameter covers the sea and the rim (making the true diameter of the sea a little less than 10 cubits), while the circumference of the sea is taken as the inside of the rim. A mystical explanation is much more enticing: due to the peculiarities of Hebrew pronunciation and spelling, the word ‘line’, or
, or 3. Many excuses have been given for the Bible’s inaccurate value, such as the claim that the sea was in a circular vessel with a thick rim. In this case the quoted 10-cubit diameter covers the sea and the rim (making the true diameter of the sea a little less than 10 cubits), while the circumference of the sea is taken as the inside of the rim. A mystical explanation is much more enticing: due to the peculiarities of Hebrew pronunciation and spelling, the word ‘line’, or
qwh
, is pronounced
qw
. Totting up the numerological values of the letters gives 111 for
qwh
and 106 for
qw
. Multiplying three by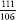 gives 3.1415, which is pi correct to five significant figures.
gives 3.1415, which is pi correct to five significant figures.
The first genius whose extreme passion for discovery about pi does justice to the aspirations of Givenchy’s aftershave is equally the man who took the most famous bath in the history of science. Archimedes slipped into the tub and noticed that the volume of water he displaced was equal to the volume of his own body under the water. He instantly realized that he could therefore find the volume of any object by submersing it, in particular the crown of the King of Syracuse, and so would be able to ascertain if that piece of royal bling was made of pure gold or not by working out its density. (It wasn’t.) As a result, he ran naked into the streets shouting ‘Eureka! [I have found it!]’, thus displaying – for the citizens of Syracuse, at least – the eternal masculine. Archimedes loved to grapple with problems in the real world, unlike Euclid, who dealt uniquely in abstractions. His many inventions were said to have included a giant catapult and a system of huge mirrors that reflected the sun’s rays with such intensity that they set Roman ships ablaze during the Siege of Syracuse. He was also the first person to come up with an apparatus to capture pi.
To do so he first drew a circle, and then he constructed two hexagons – one that he fitted inside the circle, and one that he put outside it, as in the diagrams below. This already tells us that pi must be somewhere between 3 and 3.46, which is determined by calculating the perimeters of the hexagons. If we let the diameter of the circle be 1, then the perimeter of the inner hexagon is 3, which is less than the circumference of the circle, which is pi, which is less than the perimeter of the outer one, which is 3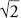 , or 3.46 to two decimal places. (The way that Archimedes calculated this value was by using a method that was essentially a fiddly precursor to trigonometry, and which is too complicated to go into here.)
, or 3.46 to two decimal places. (The way that Archimedes calculated this value was by using a method that was essentially a fiddly precursor to trigonometry, and which is too complicated to go into here.)
So, 3 < pi < 3.46.

Now if you were to repeat the calculation using two regular polygons with more than six sides, you would get a narrower bound for pi. This is because the more sides that the polygons have, the closer their perimeters are to the circumference, as we can see in the diagram above that uses a 12-sided polygon. The polygons act like walls closing in on pi, squeezing it from above and from below, between narrower and narrower limits. Archimedes started with a hexagon and eventually constructed polygons of 96 sides, allowing him to calculate pi as follows: 3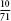 < pi < 3
< pi < 3