Alex’s Adventures in Numberland (14 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

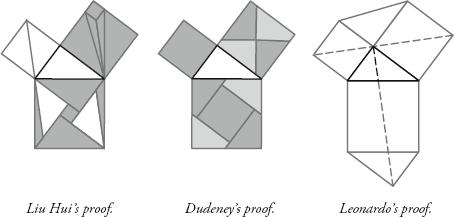
The diversity of proofs is a testament to the vitality of maths. There is never a ‘right’ way to attack a maths problem, and it’s intriguing to chart the different routes that different minds have taken in finding solutions. Above opposite are three different proofs from three different eras: one by Liu Hui, a Chinese mathematician from the third century ce, one by Leonardo da Vinci (1452–1519) and the third by Henry Dudeney, Britain’s most famous puzzlist, dated 1917. Both Liu Hui and Dudeney’s are ‘dissection proofs’ in which the two small squares are divided into shapes that can be reassembled perfectly in the big square. Leonardo’s needs a little more thought. (If you need help, see the
appendix
again.)
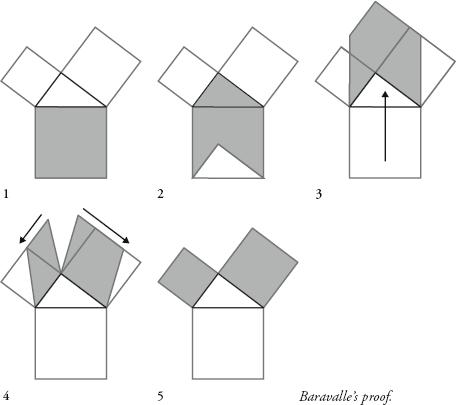
A particularly dynamic proof was devised by the mathematician Hermann Baravalle, shown below opposite. There is something more organic about this one – it shows how the big square, like an amoeba, divides itself into the two smaller ones. At each stage, the area shaded is the same. The only step that isn’t obvious is step 4. When a parallelogram is ‘sheared’, or moved in such a way that preserves the base and altitude, its area stays the same.
Baravalle’s proof is similar to the most established one in mathematical literature, that set out by Euclid around 300
BC
.
Euclid, the next most famous Greek mathematician after Pythagoras, lived in Alexandria, the city founded by the man who never abbreviated his name to Alex the Great. His
chef-d’œuvre
,
The Elements
, contained 465 theorems that summarized the extent of Greek knowledge at that time. Greek mathematics was almost entirely geometry – derived from their words for ‘earth’ and ‘measurement’ – although
The Elements
was not concerned with the real world. Euclid was operating in an abstract domain of points and lines. All he allowed in his toolkit was a pencil, a ruler and a compass, which is why they have been the fundamental components of children’s pencil cases for centuries.
Euclid’s first task (Book 1, Proposition 1) was to show that, given any line, he could make an equilateral triangle, i.e. a triangle with three equal sides, with that line as one side:
Step 1:
Put the compass point on one end of the given line and draw a circle that passes through the other end of the line.
Step 2:
Repeat the first step with the compass on the other end of the line. You now have two intersecting circles.
Step 3:
Draw a line from one of the intersections of the circle to the end points of the original line.
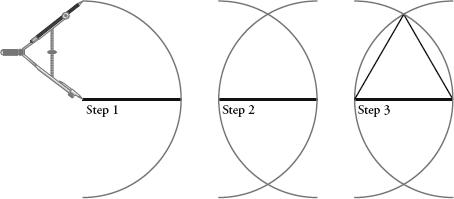
The Elements
, Proposition 1.
He then meticulously progressed from proposition to proposition, revealing a host of properties of lines, triangles and circles. For example, Proposition 9 shows how to ‘bisect’ an angle, that is construct an angle that is exactly half of a given angle. Proposition 32 states that the internal angles of a triangle always add up to two right angles, or 180 degrees.
The Elements
is a
magnum opus
of pedantry and rigour. Nothing is ever assumed. Every line follows logically from the line before. Yet from only a few basic axioms, Euclid amassed an impressive body of compelling results.
The grand finale of the first book is Proposition 47. The commentary from a 1570 edition of the first English translation reads: ‘This most excellent and notable Theoreme was first invented of the greate philosopher Pithagoras, who for the exceeding ioy conceived of the invention thereof, offered in sacrifice an Oxe, as recorde Hierone, Proclus, Lycius, & Vitruvius. And it hath bene commonly called of barbarous writers of the latter time Dulcarnon.’ Dulcarnon means two-horned, or ‘at wit’s end’ – possibly because the diagram of the proof has two horn-like squares, or possibly because understanding it is indeed horribly difficult.
There is nothing pretty about Euclid’s proof of Pythagoras’s Theorem. It is long, meticulous and convoluted, and requires a diagram full of lines and superimposed triangles. Arthur Schopenhauer, the nineteenth-century German philosopher, said it was so unnecessarily complicated that it was a ‘brilliant piece of perversity’. To be fair to Euclid, he was not trying to be playful (as was Dudeney), or aesthetic (as was Annairizi) or intuitive (as was Baravalle). Euclid’s driving concern was the of his deductive system.
While Pythagoras saw wonder in numbers, Euclid in
The Elements
reveals a deeper beauty, a watertight system of mathematical truths. On page after page he demonstrates that mathematical knowledge is of a different order than any other. The propositions of
The Elements
are true in perpetuity. They do not become less certain, or indeed less relevant with time (which is why Euclid is still taught at school and why Greek playwrights, poets and historians are not). The Euclidean method is awe-inspiring. The seventeenth-century English polymath Thomas Hobbes is said to have glanced at a copy of
The Elements
that lay open in a library when he was a 40-year-old man. He read one of the propositions and exclaimed: ‘By God, this is impossible!’ So, he read the previous proposition, and then the one before that, and so on, until he was convinced it all made sense. In the process, he fell in love with geometry for the certainty it prescribed, and the deductive approach influenced his most famous works of political philosophy. Since
The Elements
, logical reasoning has been the gold standard of all human enquiry.
Euclid started off by carving up two-dimensional space into the family of shapes known as polygons, which are those shapes made from only straight lines. With his compass and straightedge he was able to construct not just an equilateral triangle, but also a square, a pentagon and a hexagon. Polygons for which every side has the same length and the angles between the sides are all equal are called
regular polygons
. Interestingly, Euclid’s method, however, is not effective for all of them. The heptagon (seven sides), for example, cannot be constructed with a compass and straightedge. The octagon
is
constructible, but then the nonagon again is not. Meanwhile, the staggeringly complex regular polygon that has 65,537 sides is constructible, and in fact has been constructed. (It was chosen because the number is equal to 2
16
+ 1). In 1894 it took Johann Gustav Hermes, a German mathematician, ten years to do it.
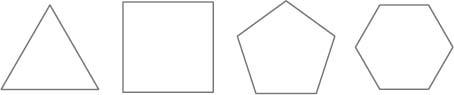
Regular polygons.
One of Euclid’s pursuits was to investigate the three-dimensional shapes that can be made from joining identical regular polygons together. Only five shapes fit the bill: the tetrahedron, the cube, the octahedron, the icosahedron and the dodecahedron, the quintet known as the Platonic solids since Plato wrote about them in the
Timaeus
. He equated them with the four elements of the universe plus the heavenly space that surrounds them all. The tetrahedron was fire; the cube, earth; the octahedron, air; the icosahedron, water; and the dodecahedron, the encompassing dome. The Platonic solids are particularly interesting because they are perfectly symmetrical. Twist them, roll them, invert them or flip them and they always stay the same.

The Platonic solids.
In the thirteenth and final book of
The Elements
, Euclid proved why there are only five Platonic solids by working out all the possible solid objects that can be made from regular polygons, starting with the equilateral triangle, and then moving on to squares, pentagons, hexagons and so on. The diagram overleaf shows how he reached his conclusion. To make a solid object from polygons you must alwys have a point where three sides meet, a corner, or what’s called a vertex. When you join three equilateral triangles at a vertex, for example, you get a tetrahedron (A). When you join four, you get a pyramid (B). A pyramid is not a Platonic solid because not all the sides are the same, but by sticking an inverted pyramid on the bottom you get an octahedron, which is. Join five equilateral triangles together and you have the first part of an icosahedron (C). But join six and you get…a flat piece of paper (D). You cannot make a solid angle with six equilateral triangles, so there are no other ways to create a different Platonic solid made up of them. Continuing this procedure with squares, it is evident that there is only one way to join three squares at a corner (E). This will end up as a cube. Join four squares and you get…a flat piece of paper (F). No more Platonic solids here. Similarly, three pentagons together give a solid angle, which becomes the dodecahedron (G). It is impossible to join four pentagons. Three hexagons meeting at the same point lie flat alongside each other (H), so it is impossible to make a solid object out of them. There are no more Platonic solids since it is impossible to join three regular polygons of more than six sides at a vertex.
