Alex’s Adventures in Numberland (18 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Again, this is very simple to carry out, and reveals a beautiful geometric order. Every intersection is on the primary creases, as F shows. (The diagram shows the seven intersections that are inside the original square; the other four are on extensions of the folds.) The first fold was random, yet all the folds meet with perfect concision and regularity on diagonals and midlines.
It struck me that if any man can be said to embody the soul of Pythagoras in the modern world, it is surely Kazuo Haga. Both men share a passion for mathematical discovery based on a wonder for the simple harmonies of geometry. The experience seemed to have touched Haga spiritually, the same way it did Pythagoras two millennia ago. ‘Most of the Japanese are trying to create new shapes in mi,’ said Haga. ‘My aim was to escape from the idea that you have to create something physical, and instead discover mathematical phenomena. That is why I find it so interesting. You find that in the very, very simple world you can still discover fascinating things.’

Every year the Indian seaside town of Puri fills with a million pilgrims. They come for one of the most spectacular festivals in the Hindu calendar – the Rath Yatra, in which three chariots the size of carnival floats are pulled through the town. When I visited, the streets were crowded with cymbal-crashing, mantra-chanting devotees, barefoot holy men with long beards and middle-class Indian tourists with fashionable T-shirts and neon saris. It was midsummer, the beginning of the monsoon season, and in between downpours festival-workers sprayed the faces of passers-by with water to cool them down. Smaller Rath Yatra processions take place simultaneously all over India, although Puri’s is the focal event and its chariots the biggest.
The festival gets under way only when the local holy man, the Shankaracharya of Puri, stands in front of the crowds and blesses them. The Shankaracharya is one of Hinduism’s most important sages, the head of a monastic order that dates back more than a thousand years. He was also the reason I had travelled to Puri. As well as being a spiritual leader, the Shankaracharya is a published mathematician. I was also a pilgrim in search of enlightenment.
Right away in India, I noticed something unfamiliar about their use of numbers. In my hotel reception I picked up a copy of
The Times of India
. With the paper’s corners flapping from gusts of competing metal fans, the front-page headline caught my eye:
5 crore more Indians
than govt thought
Crore
is the Indian-English word for ten million, so the article was saying that India had just discovered 50 million citizens it never knew it had – a number roughly comparable to the population of England. It was startling that a country could overlook such a large number, even if it represented less than 5 percent of the overall population. Yet I was more puzzled by the word
crore
. Indian English has different words for high numbers than British or American English. For example, the word ‘million’ is not used. A million is instead expressed as
ten lakh
, where
lakh
is 100,000. Since ‘million’ is unheard of in India, the Oscar-winning film
Slumdog Millionaire
was released there as
Slumdog Crorepati
. A very rich person is someone who has a crore of dollars or rupees, not a million of them. The table of Indian equivalents for British/American number words is as follows:

Note that above a thousand, Indians introduce a comma after every two digits, while in the rest of the world the convention is every three.
The use of
lakh
and
crore
is a legacy of the mathematics of ancient India. The words come from the Hindi
lakh
and
karod
, which in turn came from the Sanskrit words for those numbers,
laksh
and
koti
. In ancient India coining words for large numbers was a scientific and religious preoccupation. For example, in the
Lalitavistara Sutra
, a Sanskrit text that dates from the beginning of the fourth century at the latest, the Buddha is challenged to express numbers higher than a hundred
koti
. He replies:
One hundred
koti
are called an
ayuta
, a hundred
ayuta
make a
niyuta
, a hundred
niyuta
make a
kankara
, a hundred
kankara
make a
vivara
, a hundred
vivara
are a
kshobhya
, a hundred
kshobhya
make a
vivaha
, a hundred
vivaha
make a
utsanga
, a hundred
utsanga
make a
bahula
, a hundred
bahula
make a
nâgabala
, a hundred
nâgabala
make a
titilambha
, a hundred
titilambha
make a
vyavasthânaprajñapati
, a hundred
vyavasthânaprajñapati
make a
hetuhila
, a hundred
hetuhila
make a
karahu
, a hundred
karahu
make a
hetvindriya
, a hundred
hetvindriya
make a
samâptalambha
, a hundred
samâptalambha
make a
gananâgati
, a hundred
gananâgati
make a
niravadya
, a hundred
niravadya
make a
mudrâbala
, a hundred
mudrâbala
make a
sarvabala
, a hundred
sarvabala
make a
visamjñagati
, a hundred
visamjñagati
make a
sarvajña
, a hundred
sarvajña
make a
vibhutangamâ
, a hundred
vibhutangamâ
make a
tallakshana
.
Just as in contemporary India, the Buddha went up the list in multiples of a hundred. Since a
koti
is ten million, the value of a
tallakshana
is ten million multiplied by a hundred 23 times, which works out as 10 followed by 52 zeros, or 10
53
. This is a phenomenally large number, so large, in fact, that if you measure the entire universe from end to end in metres, and then square that number, you are roughly around 10
53
.
But Buddha didn’t stop there. He was just warming up. He explained that he had described only the
tallakshana
counting system, and above it there was another one, the
dhvajâgravati
system, made up of the same number of terms. And above that, another one, the
dhavjâgranishâmani
, again with 24 number words. In fact, there were another six systems to go – which the Buddha, of course, listed perfectly. The last number in the final system is equivalent to 10
421
: one followed by 421 zeros.
It is worth taking a breath to consider the view. There are an estimated 10
80
atoms in the universe. If we take the smallest measurable unit of time – known as Planck time, which is a second divided into 10
43
parts – then there have been about 10
60
units of Planck time since the Big Bang. If we multiply the number of atoms in the universe by the number of Planck times since the Big Bang – which gives us the number of unique positions of every particle since time began – we are still only on 10
140
, which is way, way smaller than 10
421
. The Buddha’s big number has no practical application – at least not for counting things that exist.
Not only was the Buddha able to fathom the impossibly large, he was also proficient in the realm of the impossibly tiny, explaining how many atoms there were in the
yojana
, an ancient unit of length around 10km. A
yojana
, he said, was equivalent to:
Four
krosha
, each of which was the length ofOne thousand arcs
, each of which was the length ofFour cubits
, each of which was the length ofTwo spans
, each of which was the length ofTwelve phalanges of fingers
, each of which was the length ofSeven grains of barley
, each of which was the length ofSeven mustard seeds
, each of which was the length ofSeven poppy seeds
, each of which was the length ofSeven particles of dust stirred up by a cow
, each of which was the length ofSeven specks of dust disturbed by a ram
, each of which was the length ofSeven specks of dust stirred up by a hare
, each of which was the length ofSeven specks of dust carried away by the wind
, each of which was the length ofSeven tiny specks of dust
, each of which was the length ofSeven minute specks of dust
, each of which was the length ofSeven particles of the first atoms
.
This was, in fact, a pretty good estimate. Just say that a finger is 4cm long. The Buddha’s ‘first atoms’ are, therefore, 4cm divided by seven ten times, which is 0.04m×7
–10
or 0.0000000001416m, which is more or less the size of a carbon atom.
The Buddha was by no means the only ancient Indian interested in the incredibly large and the unfeasibly small. Sanskrit literature is full of astronomically high numbers. Followers of Jainism, a sister religion to Hinduism, defined a
raju
as the distance covered by a god in six months if he covers 100,000 yojana in each blink of his eye. A
palya
was the amount of time it takes to empty a giant
yojana
-sized cube filled with the wool of newborn lambs if one strand is removed every century. The obsession with high (and low) numbers was metaphysical i nature, a way of groping towards the infinite and of grappling with life’s big existential questions.
Before Arabic numerals became an international lingua franca, humans had many other ways of writing down numbers. The first number symbols that emerged in the West were notches, cuneiform bird tracks and hieroglyphics. When languages developed their own alphabets, cultures began to use letters to represent numbers. The Jews used the Hebrew aleph (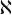 ) to mean one, bet (
) to mean one, bet (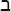 ) to be two and so on. The tenth letter, yod (
) to be two and so on. The tenth letter, yod ( ), was ten, after which each letter went up in tens, and on reaching 100 went up in hundreds. The twenty-second and final letter of the Hebrew alphabet, tav (
), was ten, after which each letter went up in tens, and on reaching 100 went up in hundreds. The twenty-second and final letter of the Hebrew alphabet, tav (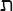 ), was 400. Using letters for numbers was confusing and also encouraged a numerological approach to counting. Gematria, for example, was the practice of adding up the numbers of the letters in Hebrew words to find a value and using this number for speculations and divinations.
), was 400. Using letters for numbers was confusing and also encouraged a numerological approach to counting. Gematria, for example, was the practice of adding up the numbers of the letters in Hebrew words to find a value and using this number for speculations and divinations.
