Alex’s Adventures in Numberland (6 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Approximate addition and comparison.
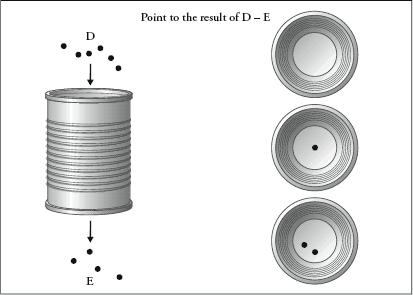
Exact subtraction.
The fact, however, that there were some Munduruku who had learned to count in Portuguese but still failed to grasp basic arithmetic was an indication of just how powerful their own mathematical system was and how well suited it was to their needs. It also showed how difficult the conceptual leap must be to having a proper understanding of exact numbers above five.
Could it be that humans need words for numbers above four in order to have an exact understanding of them? Professor Brian Butterworth, of University College London, believes that we don’t. He thinks that the brain contains a ready-built capacity to understand exact numbers, which he calls the ‘exact number module’. According to his interpretation, humans understand the exact number of items in small collections, and by adding to these collections one by one we can learn to understand how bigger numbers behave. He has been conducting research in the only place outside the Amazon where there are indigenous groups with almost no number words: the Australian Outback.
The Warlpiri aboriginal community live near Alice Springs and have words only for one, two and many, and the Anindilyakwa of Groote Eylande in the Gulf of Carpentaria have words only for one, two, three (which sometimes means four) and many. In one experiment with children of both groups, a block of wood was tapped with a stick up to seven times and counters were placed on a mat. Sometimes the number of taps matched the number of counters, sometimes not. The children were perfectly able to say when the numbers matched and when they didn’t. Butterworth argued that to get the answer right the children were producing a mental representation of exact number that was abstract enough to represent both auditory and visual enumeration. These children had no words for the numbers four, five, six and seven, yet were perfectly able to hold those amounts in their heads. Words were useful to understand exactness, Butterworth concluded, but not necessary.
Another important focus of Butterworth’s work – and of Stanislas Dehaene’s – is a condition called
dyscalculia
, or number blindness, in which one’s number sense is defective. It occurs in an estimated 3–6 percent of the population. Dyscalculics do not ‘get’ numbers the way most people do. For example, which of these two figures is biggest?
65 24
Easy, it’s 65. Almost all of us will get the correct answer in less than half a second. If you have dyscalculia, however, it can take up to three seconds. The nature of the condition varies from person to person, but those diagnosed with it often have problems in correlating the symbol for a number, say 5, with the number of objects the symbol represents. They also find it hard to count. Dyscalculia does not mean you cannot count, but suffereEasd to lack basic intuitions about number and instead rely on alternative strategies to cope with numbers in everyday life, for instance by using their fingers more. Severe dyscalculics can barely read the time.
If you were smart in all your subjects at school but failed ever to pass an exam in maths, you may well be dyscalculic. (Although if you always failed at maths, you are probably not reading this book.) The condition is thought to be a principal cause of low numeracy. Understanding dyscalculia has a social urgency, since adults with low numeracy are much more likely to be unemployed or depressed than their peers. Yet dyscalculia is little understood. It can be thought of as the number version of dyslexia; the conditions are comparable in that they both affect roughly the same proportion of the population and they appear to have no bearing on overall intelligence. However, a lot more is known about dyslexia than about dyscalculia. It is estimated, in fact, that academic papers on dyslexia outnumber those on dyscalculia by about ten to one. Among the reasons why dyscalculia research is so far behind is that there are many
other
reasons why one might be bad at maths – the subject is often taught badly at school, and it is easy to fall behind if you miss lessons when crucial concepts are introduced. There is also less of a social taboo around being rubbish with numbers than there is around being rubbish at reading.
Brian Butterworth frequently writes references for people he has tested for dyscalculia, explaining to prospective employers that the failure to achieve school maths qualifications is not due to laziness or lack of intelligence. Dyscalculics can be high achievers in all other areas beyond numbers. It is even possible, says Butterworth, to be dyscalculic and very good at maths. There are several branches of mathematics, such as logic and geometry, that prioritize deductive reasoning or spatial awareness rather than dexterity with numbers or equations. Usually, however, dyscalculics are not at all good at maths.
Much of the research into dyscalculia is behavioural, such as the screening of tens of thousands of schoolchildren by giving them tests on a computer in which they must say which of two numbers is the biggest. Some is neurological, in which magnetic resonance scans of dyscalculic and non-dyscalculic brains are studied to see how their circuitry differs. In cognitive science, advances in understanding a mental faculty often come from studying cases where the faculty is faulty. Gradually, a clearer picture is emerging of what dyscalculia is – and of how the number sense works in the brain.
Neuroscience, in fact, is providing some of the most exciting new discoveries in the field of numerical cognition. It is now possible to see what happens to individual neurons in a monkey’s brain when that monkey thinks of a precise number of dots.
Andreas Nieder at the University of Tübingen in southern Germany trained rhesus macaques to think of a number. He did this by showing them one set of dots on a computer, then, after a one-second interval, showing another set of dots. The monkeys were taught that if the second set was equal to the first set, then pressing a lever would earn them a reward of a sip of apple juice. If the second set was not equal to the first, then there was no apple juice. After about a year, the monkeys learned to press the lever only when the number of dots on the first and second screens was equal. Nieder and his colleagues reasoned that during the one-second interval between screens the monkeys were thinking about the number of dots they had just seen.
Nieder decided he wanted to see what was happening in the monkeys’ brains hey were holding the number in their heads. So, he inserted an electrode two microns in diameter through a hole in their skulls and into the neural tissue. Don’t worry, no monkeys were hurt. At that size, an electrode is tiny enough to slide through the brain without causing damage or pain. (The insertion of electrodes into human brains for research contravenes ethical guidelines, although it is allowed for therapeutic reasons such as the treatment of epilepsy.) Nieder positioned the electrode so that it faced a section of the monkeys’ pre-frontal cortex, and then began the experiment.
The electrode was so sensitive that it could pick up electrical discharge in individual neurons. When the monkeys thought of numbers, Nieder saw that certain neurons became very active. A whole patch of their brains was lighting up.
On closer analysis, he made a fascinating discovery. The number-sensitive neurons reacted with varying charges depending on the number that the monkey was thinking of at the time. And each neuron had a ‘preferred’ number – a number that made it most active. There was, for example, a population of several thousand neurons that preferred the number one. These neurons shone brightly when a monkey thought of one, less brightly when he thought of two, even less brightly when he thought of three, and so on. There was another set of neurons that preferred the number two. These neurons shone brightest when a monkey thought of two, less brightly when he thought of one or three, dimmer still when the monkey thought of four. Another group of neurons preferred the number three, and another the number four. Nieder conducted experiments up to the number 30, and for each number found neurons that preferred that number.
The results offered an explanation for why our intuitions favour an approximate understanding of numbers. When a monkey is thinking ‘four’, the neurons that prefer four are the most active, of course. But the neurons that prefer three and the neurons that prefer five are also active, though less so, because its brain is also thinking of the numbers surrounding four. ‘It is a noisy sense of number,’ explained Nieder. ‘The monkeys can only represent cardinalities in an approximate way.’
It is almost certain that the same thing happens in human brains. Which raises an interesting question. If our brains can represent numbers only approximately, then how were we able to ‘invent’ numbers in the first place? ‘The “exact number sense” is a [uniquely] human property that probably stems from our ability to represent number very precisely with symbols,’ concluded Nieder. Which reinforces the point that numbers are a cultural artefact, a man-made construct rather than something that we acquire innately.

In Lincolnshire during medieval times, a
pimp
plus a
dik
got you a
bumfit
. There was nothing dishonourable about this. The words were simply the numbers five, ten and fifteen in a jargon used by shepherds when counting their sheep. The full sequence ran:
- Yan
- Tan
- Tethera
- Pethera
- Pimp
- Sethera
- Lethera
- Hovera
- Covera
- Dik
- Yan-a-dik
- Tan-a-dik
- Tethera-dik
- Pethera-dik
- Bumfit
- Yan-a-bumfit
- Tan-a-bumfit
- Tethera-bumfit
- Pethera-bumfit
- Piggot
This is a different way from how we count now, and not just because all the words are unfamiliar. Lincolnshire shepherds organized their numbers in groups of twenty, starting counting with
yan
and ending with
piggot
. If a shepherd had more than twenty sheep – and provided he hadn’t sent himself to sleep – he would make note of having completed one cycle by putting a pebble in his pocket, or making a mark on the ground, or scraping a line in his crook. He would then start from the beginning again:
‘Yan, tan, tethera…’
If he had 80 sheep, he would have four pebbles in his pocket, or have marked four lines, at the end. The system is very efficient for the shepherd; he has four small items to represent 80 big ones.
In the modern world, of course, we group our numbers in tens, so our number system has ten digits – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The number of the counting group, which is often also the number of symbols used, is called the base of a number system, so our decimal system is base ten, while the shepherds’ base is 20.
Without a sensible base, numbers are unmanageable. Imagine that the shepherd had a base-one system, which would mean he had only one number word:
yan
for one. Two would be
yan yan
. Three would be
yan yan yan
. Eighty sheep would be
yan
said 80 times. This system is pretty useless for counting anything above about three. Alternatively, imagine that every number was a separate word so that being able to count up to 80 would require memory for 80 unique words. Now count to a thousand this way!
Many isolated communities still use unconventional bases. The Arara in the Amazon, for example, count in pairs, with the numbers from one to eight as follows:
anane, adak, adak anane, adak adak, adak adak anane, adak adak adak, adak adak adak anane, adak adak adak adak
. Counting in twos is not much of an improvement over counting in ones. Expressing 100 requires repeating
adak
50 times in succession – which would make haggling at the market rather time-consuming. Systems in which numbers are grouped in threes and fours are also found in the Amazon.
The trick of a good base system is that the base number needs to be large enough to be able to express numbrs like 100 without running out of breath, but not so large that we need to overexercise our memories. The most common bases throughout history have been five, ten and twenty, and there is an obvious reason why. These numbers are derived from the human body. We have five fingers on one hand, so five is the first obvious place to take a breath when counting upwards from one. The next natural pause comes at two hands, or ten fingers, and after that at hands and feet, or twenty fingers and toes. (Some systems are composite. The Lincolnshire sheep-counting lexicon, for example, contains base five and ten as well as base 20: the first ten numbers are unique, and the next ten are grouped in fives.) The role that fingers have played in counting is reflected in much number vocabulary, not least the double meaning of digit. For example, five in Russian is
piat
, and the word for outstretched hand is
piast
. Similarly, Sanskrit for the word five,
pantcha
, is related to the Persian
pentcha
, hand.
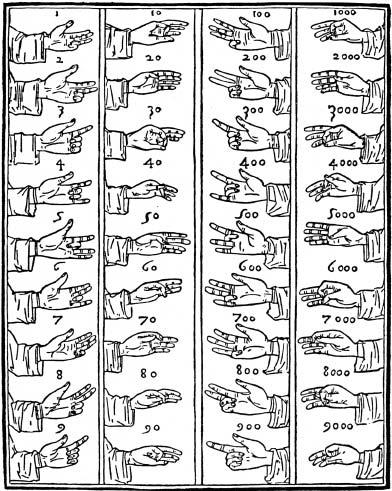
Finger counting from Luca Pacioli’s
Summa de arithmetica, geometria, proportioni et proportionalita
(1494).
From the moment man started to count he was using his fingers as an aid, and it is no exaggeration to credit a great deal of scientific progress to the versatility of our fingers. If humans were born with flat stumps at the ends of our arms and legs, it is fair to speculate that we would not have evolved intellectually beyond the Stone Age. Before the widespread availability of paper and pencil allowed numbers to be easily written down, they were often communicated through elaborate finger-counting sign languages. In the eighth century the Northumbrian theologian the Venerable Bede presented a system to count to a million, which was one part arithmetic, one part jazz hands. Units and tens were represented by the left fingers and thumb; hundreds and thousands on the right. Higher orders were expressed by moving the hands up and down the body – with a rather unpriestly image to represent 90,000: ‘grasp your loins with the left hand, the thumb towards the genitals’, Bede wrote. Much more evocative was the sign for a million, a self-satisfied gesture of achievement and closure: the hands clasped together, fingers intertwined.
Until only a few hundred years ago, no manual of arithmetic was complete without diagrams of finger-counting. Now, while mostly a lost art, the practice continues in some parts of the world. Traders in India who want to conceal their dealings from bystanders use a method of touching knuckles behind a cloak or cloth. In China, an ingenious – if rather overly intricate – technique allows you to count up to one less than ten billion – 9,999,999,999. Each finger has nine imaginary points – three on each crease line, as marked on the diagram opposite. These points on the right little finger represent the digits 1 to 9. The points on the right fourth finger take us from 10 to 90. The right middle finger goes from 100 to 900, and so on, with each new finger representing the next power of ten. It is therefore possible to count every single person on Earth with only your fingers, which is one way to have the whole world in your hands.
Some cultures count using more of their bodies than just fingers and toes. At the end of the nineteenth century an expedition of British anthropologists reached the islands of the Torres Strait, the stretch of water that separates Australia from Papua New Guinea. There they discovered a community that started with ‘right hand little finger’ for 1, ‘right hand ring finger’ for 2 and this continued through the fingers to ‘right wrist’ for 6, ‘right elbow’ for 7 and on through the shoulders, sternum, left arm and hand, feet and legs, ending at ‘right foot little toe’ for 33. Subsequent expeditions and research uncovered many communities in the region with similar ‘body-tally’ systems.
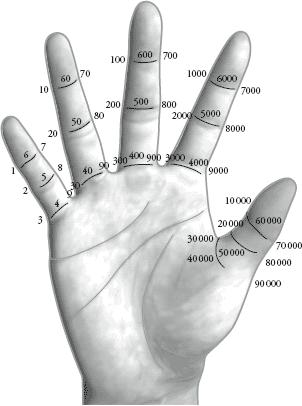
In this Chinese system, each finger has nine points, representing the digits 1 to 9 for each order of magnitude, so the right hand can express any number up to 10
5
– 1 when the other hand touches the relevant points. Swapping hands, the numbers continue to 10
10
– 1. A ‘zero’ point is not needed on any finger, since when there are no values relating to that finger it is simply left alone by the other hand.
Perhaps the most curious is the Yupno, the only Papuan people for whom each individual owns a short melody that belongs to them like a name, or signature tune. They also have a counting system that enumerates the nostrils, eyes, nipples, belly button and climaxes in 31, for ‘left testicle’, 32, ‘right testicle’ and 33, ‘penis’. While one can ponder the significance of 33 in the three great monotheistic religions (the age when Christ died, the length of King David’s reign and the number of individual beads on a Muslim prayer string), what is particularly intriguing about the Yupno’s phallic number is that they are actually very coy about it. They refer to the number 33 euphemistically in phrases such as ‘the man thing’. Researchers were unable to discover whether women use the same terms, since they are not supposed to know the number system and refused to answer questions. The upper limit in Yupno is 34, which they call ‘one dead man’.
Base-ten systems have been used in the West for thousands of years. Despite their harmoniousness with our bodies, however, many have questioned whether they are the most sensible base for counting. In fact, some have argued that their physical provenance makes them an actively
bad
choice. King Charles XII of Sweden dismissed base ten as the product of ‘rustic and simple people’ fumbling around with their fingers. In modern Scandinavia, he believed, a base was needed ‘of more convenience and greater use’. So, in 1716, he ordered the scientist Emanuel Swedenborg to devise a new counting system with a base of 64. He arrived at this formidable number due to the fact that it was derived from a cube, 4 × 4 × 4. Charles, who fought – and lost – the Great Northern War, believed that military calculations, such as measuring the volume of a box of gunpowder, would be made easier with a cube number as a base. Yet his brainwave, wrote Voltaire, ‘could prove only that he loved the extraordinary and the difficult’. Base 64 requires 64 unique names (and symbols) for numbers – an absurdly inconvenient system. Swedenborg therefore simplified the system to base eight and came up with a new notation in which 0, 1, 2, 3, 4, 5, 6, 7 were renamed o, l, s, n, m, t, f, u. In this system, therefore l + l = s, and m × m = so. (The words for the new numbers, however, were rather wonderful. The powers of 8, which would have been written lo, loo, looo, loooo and looooo, were to be pronounced, or yodelled,
lu, lo, li, le
and
la
.) In 1718, however, shortly before Swedenborg was due to present the system, a bullet shot the king – and his octonary dream – stone dead.

One dead Yupno.
But Charles XII had a valid point. Why should we stick with the decimal system just because it was derived from the number of our fingers and toes? If humans were like Disney characters, for example, and had only three fingers and a thumb per hand, it is almost certain that we would live in a base-eight world: giving marks out of eight, compiling top eight charts and letting eight cents make a dime. Mathematics would not change by having an alternative way to group numbers. The bellicose Swede was correct to ask which base best suits our scientific needs – rather than opting for the one that suits our anatomy.
In late 1970s Chicago, Michael de Vlieger was watching the cartoons on Saturday morning TV. A short segment came on. The soundtrack was of disconcerting, off-key piano chords, wah-wah guitar and a menacing bass. Under a full moon and starry night sky a strange humanoid appeared. He had a blue and white striped top hat and tails, blond hair and a stick nose, rather in keeping with the glam-rock fashion of the era. If that wasn’t creepy enough, he had five fingers and a thumb on each hand, and six toes on each foot. ‘It was a little freaky, kind of spooky,’ remembered Michael. The cartoon was
Little Twelvetoes
, an educational broadcast about base 12. ‘I think the majority of the American population had no idea what was going on. But I thought it was so cool.’
