100 Essential Things You Didn't Know You Didn't Know (22 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

fn2
n
C
g
is shorthand for n!/g!(n–g)! and is the number of ways of choosing g outcomes from a total of n possibilities.
69
Playing Fair with a Biased Coin
And somewhat surprisingly, Cambridge have won the toss.
Harry Carpenter
Sometimes you need a fair coin to toss so that you can make a choice between two options without any bias. At the outset of many sports events, the referee tosses a coin and asks one of the competitors to call ‘heads’ or ‘tails’. You could set up gambling games by scoring sequences of coin tosses. You could use more than one coin simultaneously, so as to create a greater number of possible outcomes. Now suppose that the only coin that you have available is a biased one: it does not have an equal probability (of ½) of falling ‘heads’ or ‘tails’. Or perhaps you just suspect that the coin that your opponent has so thoughtfully provided might not be fair. Is there anything you can do in order to ensure that tossing a biased coin creates two equally likely, unbiased outcomes?
Suppose that you toss the coin twice and ignore outcomes where both outcomes are the same – that is, toss again if the sequence ‘heads-heads’ (HH) or ‘tails-tails’ (TT) happens. There are two pairs of outcomes that could result: ‘heads’ followed by ‘tails’ (HT), or ‘tails’ followed by ‘heads’ (TH). If the probability of the biased coin coming down ‘heads’ is p, then the probability of getting ‘tails’ is 1−p, and so the probability of getting the sequence HT
is
p(1−p) and that of getting TH is (1−p)p. These two probabilities are the same, regardless of the probability p of the biased coins. All we have to do to get a fair game is define HEADS by the sequence HT and TAILS by the sequence TH, and the probability of TAILS is the same as the probability of HEADS. And you don’t need to know the bias, p, of the coin.
fn1
fn1
This trick was thought up by the great mathematician, physicist and computer pioneer, John von Neumann. It had wide use in the construction of computer algorithms. One of the questions that was subsequently addressed was whether there were more efficient ways of defining the new HEAD and TAIL states. The way we have done it wastes ‘time’ by having to discard all the HH and TT outcomes.
70
The Wonders of Tautology
A good guide to understanding events in the modern world is to assume the opposite of what Lord Rees-Mogg tells you is the case.
Richard Ingrams
‘Tautology’ is a word that gives out bad vibes. It suggests meaninglessness, and my dictionary defines it as ‘a needless repetition of an idea, statement or word’. It is a statement that is true in all eventualities: all red dogs are dogs. But it would be wrong to think that tautologies are of no use. In some sense they may be the only way to really secure knowledge. Here is a situation where your life depends upon finding one.
Imagine you are locked in a cell that has two doors – a red door and a black door. One of those doors – the red one – leads to certain death and the other – the black one – leads to safety, but you don’t know which leads to which. Each door has a phone next to it from which you can call an adviser who will tell you which door you should take in order to get out safely. The trouble is that one adviser always tells the truth and the other always lies, but you don’t know which one you are talking to. You can ask one question. What question should you ask?
Take the simplest question you could ask: ‘Which door should
I
go through?’ The truthful adviser will tell you to go through the black one and the untruthful adviser will tell you to go through the red one. But, since you don’t know which of the advisers you are speaking to is telling the truth, this doesn’t help you. You would do just as well taking a random guess at red or black. ‘Which door should I go through?’ is not therefore a tautology in this situation. It is a question that can have different answers.
Suppose instead you asked: ‘What door would the other adviser tell me to go through?’ The situation is now more interesting. The truthful adviser knows that the lying adviser will tell you to go through the deadly red door so the truthful adviser will say that the other adviser will tell you to go through the red door. The untruthful adviser knows that the truthful adviser will tell you to go through the black door to safety and so the untruthful adviser will try to deceive you by saying you should go through the red door.
You have made a life-saving discovery. Regardless of who answers your question, you get told to go through the red door. You have stumbled upon a question that is a tautology – it always has the same answer – and that is your lifeline. Your strategy for safe escape is therefore clear: ask: ‘What door would the other adviser tell me to go through?’, note the answer (red) and then go through the other door (black) to safety.
71
What a Racket
Speed has never killed anyone, suddenly becoming stationary . . . that’s what gets you.
Jeremy Clarkson
Some things are harder than others to move. Most people think that the only thing that counts in such a problem is their weight. The heavier the load, the harder it is to shift it. But try moving lots of different types of load and you will soon discover that the concentration of the load plays a significant role. The more concentrated the mass, the easier it is to move and the faster it wobbles (recall what we learnt in Chapter 2). Look at an ice skater beginning a spin. She will begin with her arms outwards and then steadily draw them in towards her body. This results in an increasingly rapid spin rate. As the skater’s mass is more concentrated towards her centre, she moves faster. On the other hand, if you look at the shapes of girders used to build robust buildings, they have an H-shaped cross-section. This distributes more mass away from the centre of the girder and so makes it harder to move or deform the girder when it is stressed.
This resistance to being moved is called ‘inertia’, following its common usage, and it is determined by the total mass of an object and also by its distribution, which will be determined by the shape of the object. If we think still about rotation, then an interesting example is a simple object like a tennis racket. It has an unusual
shape
and can be rotated in three distinct ways. You can lay the tennis racket flat on the floor and spin it around its centre. You can stand it on its top and twist the handle. And you can hold it by the racket handle and throw it up in the air so it somersaults and returns to be caught by the handle again. There are three ways to spin it because there are three directions to space, each at right angles to the other two, and the racket can be spun around an axis pointing along any one of them. The racket behaves rather differently when spun around each of the different axes because its mass distribution is different around each axis and so it has a different inertia for motion around each axis. Here are two of them:
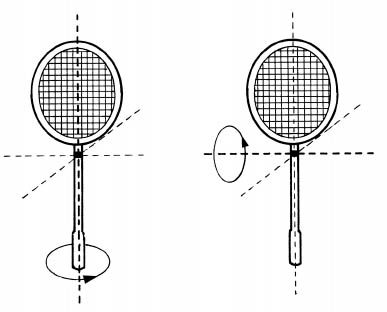
There is one remarkable property of these different motions, which is displayed by your three tosses of the racket. The motion around the axes about which the inertia is the largest or the smallest is simple. When the racket is flat on the ground or stood upright and spun, it does nothing very unusual. But when you spin it about
the
in-between axis, about which the inertia is intermediate between the largest and the smallest (shown on the right), something unusual happens. Hold the racket by the handle with the face upwards, as if you were holding a frying pan. Mark the top face with some chalk. Toss the racket so that it does a complete 360-degree turnover and catch it by the handle again. The face with the chalk mark will now be facing
downwards
.
The golden rule is that a spin around the axis with the in-between inertia is unstable. The slightest deviation from the precise centre line always causes it to flip over. Sometimes this is a good thing. If you are a gymnast doing a somersault on the beam, then you look more impressive (and score higher marks) if you do a twist as well. But the twist can happen automatically because of this instability.
A more serious example of this instability arose a few years ago on the International Space Station after it had been hit during a mistimed docking operation with a Russian supply craft. The Station was damaged and set in a slow spin. There was still gas in the system of retro rockets, which could be fired to slow the spin and return the Station to its usual state of equilibrium. The problem was, though, how should the rockets be fired? In what direction should you move the Station so as to counter the existing rotation. British astronaut Michael Foales had to solve this problem while holed up in the undamaged part of the Station with his laptop and a link to the ground. The most important things to discover were the three inertias of the Space Station with respect to rotations about its three axes. If the correcting rockets were fired wrongly, then they could set the Station spinning around its intermediate axis of inertia. The result would have been total disaster. The instability that flipped your tennis racket over had no bad effects on the racket, but flip over the Space Station and it would break apart, leaving all the astronauts dead, a quarter of a million kilograms of potentially lethal debris scattered in space and an astronomical financial loss. NASA didn’t know the three
inertias
for the Space Station – no one had thought such facts would be needed – and so Foales had to work them out from the design plans and then calculate how the Station would respond to rockets being fired in different directions in order to correct its spin from the accident. Fortunately, he knew about the instability of rotation about the intermediate axis and got all his calculations right. The dangerous spin was righted and the astronauts were saved. Maths can be a matter of life and death.
72
Packing Your Stuff
On travel: I have learnt that you need four times as much water, twice as much money and half as many clothes as you think you need at the outset.
Gavin Esler
A young boy was once shown a large empty glass jar with a screwtop lid. He was handed a box of tennis balls and asked to fill the jar. He poured in some tennis balls and then moved them around a bit to try to squeeze in another tennis ball before screwing down the lid. ‘Is the jar full?’ he was asked. ‘Yes, it’s full,’ he replied. But then he was given a box of marbles and asked to see if he could fit any more in the jar. He opened the lid and found that he could fit quite a few marbles in between the tennis balls. Giving the jar a shake now and then allowed the marbles to settle into the spaces. Eventually, he couldn’t fit in another marble and announced that the jar was now full. His mentor then produced a bag of sand and asked the boy to fill the jar. Again, he unscrewed the lid and poured the sand into the top of the jar. This time he didn’t need to fiddle around very much at all, just give the jar a careful shake now and again to make sure that the sand was pouring into all the empty nooks and crannies between the tennis balls and the marbles. Finally, he couldn’t fit any more sand in the jar and screwed the lid back down again. The jar really was full!
There are some lessons to be learned from this story. If the boy
had
been given the sand first and asked to fill up the jar, then there would not have been any room to fit in any marbles or tennis balls afterwards. You need to start with the biggest things if there is to be any room for them at all. The same applies to more familiar packing problems. If you need to move lots of packages into a van then you might want to know how you should set about loading them in order to have the best chance of getting them all in. Our little story shows why you should start with the largest objects and then pack the next largest and so on, leaving the smallest until last.
The shapes of the things you are trying to pack clearly matter. Often, they are all the same size. If you are a manufacturer of sweets or other small food items, you might want to know what shape they should be in order to fit as many as possible into a jar or some other large storage container. For a long time it was thought that the answer was to make them all little spheres, like gobstoppers. Lots of little spheres seemed to give the smallest amount of empty space in between the closely packed balls. Interestingly, it turned out that this wasn’t the best shape to use. If sweets are made in the shape of little ellipsoids, rather like mini-rugby balls or almonds, then more of the space can be filled by them. So Smarties and M&Ms fill a volume more efficiently than any collection of identical spheres. If the ellipsoids have their short to long axes in the ratio of 1 to 2, then they leave just 32% of the space empty, compared with 36% if they were made into spheres. This seemingly trivial fact has many important consequences for business efficiency and industrial manufacture, reducing wastage, shipping costs and the avoidance of unnecessary packaging.
73
Sent Packing Again
All my bags are packed; I’m ready to go.
John Denver
Our little packing problem with the jars in the previous chapter was a nice simple one. We started with the biggest objects and progressed down to the smaller ones. In practice, our problem may be more tricky. We may have lots of containers to fill up with shopping items of different sizes. How do we go about distributing the items of different sizes across the bags so as to use the smallest number of bags? ‘Packing’ might not just mean packing in space either; it can mean packing in time. Suppose you are the manager of a big copy-shop business that runs off copies of different documents of different sizes all day for customers. How do you allocate the different copying jobs to the machines so that you minimise the total number of machines that you need to complete the day’s work?
