100 Essential Things You Didn't Know You Didn't Know (21 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

Another traditional type of right-angled gallery will be divided into rooms, like this 10-roomed example:

In these cases you can always divide the galley up into a collection of non-overlapping rectangles. This is a useful design because if you place an attendent at the opening connecting two different rooms, then he can guard both of them at the same time. But no guard can guard 3 or more rooms at once. So, now the number of guards that is sufficient and occasionally necessary to keep a complete watch on the gallery is the whole number part of ½ × (Number of Rooms), or 5 for the gallery drawn here. This is a very economical use of human resources.
We have been speaking of people watching the walls, but the things we have said also apply to CCTV cameras or to lights for illuminating the gallery and its rooms. Next time you are planning to steal the
Mona Lisa
you will have a head start.
66
. . . and What About a Prison?
All my contacts with criminals show that what they’re doing is just a slightly more extreme version of what everybody is doing.
David Carter
Art galleries are not the only buildings that have to be guarded. Prisons and castles do too. But they are an inside-out version of art galleries. It is the outside walls that have to be guarded. How many guards do you need to station at the corners of a polygonal fortress in order to observe all of its exterior walls? There is a simple answer: the smallest whole number at least equal to ½ × (Number of corners). So, with 11 corners, you need 6 guards to guard the outside walls. Better still, we know it is the exact number you need. No fewer will be sufficient and no more are necessary. In the inside gallery problem, we only ever knew the largest possible number that we might need.
We can think about the case of right-angled prison walls again, as we did for the galleries. We might have an outer prison wall like these two right-angled shapes.
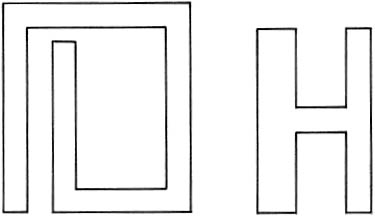
In these right-angled cases we need 1 plus the smallest whole number at least equal to ¼ × (Number of corners) to guard the whole of the outer wall. No fewer are possible and no more are needed. In the two examples shown there are 12 corners and so we need 1 + 3 = 4 guards.
67
A Snooker Trick Shot
Steve is going for the pink ball – and for those of you watching in black and white, the pink is next to the green.
Ted Lowe
Some people used to satisfy themselves that if their children spent most of their waking lives playing computer games, it was good for their understanding of maths and computing. I always wondered if they felt that hours at the snooker or pool hall were adding to their knowledge of Newtonian mechanics. Still, a knowledge of simple geometry can certainly provide you with some impressive snooker demonstrations for the uninitiated.
Suppose that you want to hit a single ball so that it goes around the table, bounces off three cushions, and returns to the point from which it was struck. Let’s start with the easy case – a square table. Everything is nice and symmetrical, and it should be clear that you should place the ball in the middle of one of the sides of the table and then strike it at an angle of 45 degrees to the side. It will hit the middle of the adjacent side at the same angle and follow a path that is a perfect square, shown dashed in the diagram overleaf.
You don’t have to start with the ball against one of the cushions, of course; if you strike it from any point on the dashed square path and send it along one of the sides of the dashed square, then the ball will eventually return to where it started (as long as you hit it hard enough). If you want it to stop at exactly the point that you hit it from, then you need to be very skilful – or at least put in a little practice.

Unfortunately, you won’t very often come across a square snooker table. Modern tables are made from two squares side by side and a full-size table will have dimensions of 3.5 m × 1.75 m. The important general feature is that the table’s length is twice its width. Using this simple fact, you can draw how your trick shot will have to run when the table has these rectangular dimensions. I have drawn in the diagonal as well for reference. Your shot has to go parallel to the diagonal and hit the sides at points that divide each of them in the ratio 2 to 1, the same ratio as the ratio of the length to the width of the table. (In the case of the square table this ratio was equal to 1 and you had to hit the centre of each side of the table.) This means that the angle that the ball’s path makes with the long sides of the table has its tangent equal to ½, or 26.57 degrees, and the angle it makes with the short sides is 90 minus this angle, or 63.43 degrees, since the three interior angles of the right-angled triangles must add up to 180 degrees. The dashed parallelogram marks the only path
on
the rectangular table that will see the ball return to its starting point.

If you find yourself playing on a non-standard table, you need to recalculate. In general, the magic angle you need to strike the ball at, relative to the long side of the table, is the angle whose tangent equals the ratio of the width to the length of the table (1:2 for our full-size table and 1:1 for the square table) and the point against the cushion you need to strike from must divide the length of the side in the same ratio as the length to the width of the table.
68
Brothers and Sisters
Sisterhood is powerful.
Robin Morgan
One of the strangest things about China is the growing consequences of the ‘one-child’ policy. With the exception of multiple births (typically 1 per cent of the total), every young person in urban areas is an only child.
fn1
In this situation, the likelihood of each child being lavished with rather too much parental attention has given rise to the term ‘Little Emperor Syndrome’. In the future, for almost everybody, there will be no brothers and sisters and no aunts or uncles. A concept like ‘fraternity’ will gradually lose all meaning.
At first, there seems to be a strange general asymmetry about brothers and sisters. If there are 2 children, one boy and one girl, then the boy has a sister but the girl doesn’t. If there are 4 children, 3 girls and one boy, then the boy has got 3 sisters and the girls between them have 3 × 2 = 6 sisters. Each girl only gets to count the other girls as sisters but the boy counts them all. So it looks as if boys should always have more sisters than girls!
This seems paradoxical. Let’s look more closely. If a family with n children has g girls and n−g boys, then the boys have a total of
g
(n−g) sisters between them, while the girls have a total of g(g−1) sisters. These numbers can only be equal if g = ½ (n+1). This can never be true when n is an even number because then g would be a fraction.
The puzzle has been created because there are many ways in which a family of children can be formed. A family of 3 children can have 3 sons, 3 daughters, 2 sons and 1 daughter, or 2 daughters and 1 son. If we assume that there is an equal chance of
1
/that a newborn child will be a boy or a girl (this is not quite true in reality) then a family of n children can be made up in 2
n
different ways. The number of different family make-ups with n children and g daughters is denoted by
fn2
n
C
g
and the boys will each have g(n–g) sisters. Given all the 2
n
different ways in which the family can be divided into sons and daughters, we should be asking what is the
average
number of sisters that the boys in the n-child families will have. This is the sum of all the answers for the number of sisters they can have for all the possible values of the number g = 0,1,2,. . ., n divided by the total number, 2
n
. This is
b
n
= 2
-n
∑
g
n
C
g
× g(n−g)
Similarly, the average number of sisters that the girls in the n-child families have is
g
n
= 2
-n
∑
g
n
C
g
× g(g−1)
The solutions to these formulae are much simpler than the formulae would lead us to expect. Remarkably, the average numbers of sisters for the boys and the girls are equal, and b
n
= g
n
= ¼ n(n−1). Notice that because it is an average, it doesn’t mean that any given family has to have the average behaviour. When
n
= 3, the average number of sisters is 1.5 (which no one family could have). When n = 4, the average number is 3. When n gets big, the number gets closer and closer to the square of n/2. Here is the table of the 8 possibilities for families with 3 children:
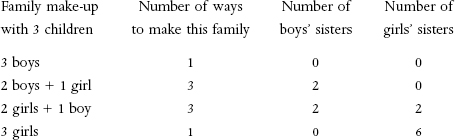
We see that the total number of sisters for the boys are the sums from the second and third rows, 3 × 2 + 3 × 2 = 12, and the total number of sisters for the girls is the sum of the third and the fourth rows; it is also 12 = 3 × 2 + 1 × 6. Since there are 8 possible ways to make this family, the average number of sisters for the girls and the boys is equal to 12/8 = 1.5, as predicted by our formula ¼ × n × (n–1) for the case of n = 3, when there are three children.
fn1
In rural areas a second child is permitted after an interval of 3 years if the first child was disabled or female.
