100 Essential Things You Didn't Know You Didn't Know (20 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

What was the trick? Simply make sure the stronger candidates eliminate each other one by one in the early stages and introduce your ‘protected’ candidate only at the last moment, ensuring that they are compared only with other candidates they can beat. So, with the right seeding, a British tennis player can win Wimbledon after all.
63
The Swing of the Pendulum
England swings like a pendulum do.
Roger Miller
The story is told that in the sixteenth century the great Italian scientist Galileo Galilei used to amuse himself by watching the swinging of the great bronze chandelier that hung from the ceiling of the cathedral in Pisa. It may have been set in motion to spread the aroma of incense, or it may have been disturbed by the need to lower it to replenish the candles. What he saw fascinated him. The rope suspending the chandelier from the ceiling was very long and so the chandelier swung backwards and forwards like a pendulum, very slowly: slow enough to time how long it would take to make a complete journey out and back to its starting point. Galileo observed what happened on many occasions. On each occasion the chandelier swung differently; sometimes making only very small swings; sometimes somewhat larger ones – but he had noticed something very important. The period of time taken by the swinging chandelier to complete a single out and back swing was the same regardless of how far it swung. Given a large push, it went further than if it were given a small one. But if it went further, it went faster and took the same time to get back to where it started from as if it were pushed very gently.
This discovery
fn1
has far-reaching consequences. If you have a grandfather clock then you will have to wind it up about once a week. Galileo’s discovery means that if the pendulum has stopped, it doesn’t matter how your push starts it swinging again. As long as the push is not too big, it will take the same time to swing back and forth and the resulting ‘tick’ will have the same duration. Were it not so, then pendulum clocks would be very tedious objects. You would have to set the amplitude of the swinging pendulum exactly right in order that the clock keeps the same time as it did before it stopped. Indeed, Galileo’s acute observation is what led to the idea of the pendulum clock. The first working version was made by the Dutch physicist Christiaan Huygens in the 1650s.
Finally, there is a nice test of whether a physicist’s logic is stronger than his survival instinct that exploits the swing of a pendulum. Imagine that we have a huge, heavy pendulum, like the cathedral chandelier that Galileo watched. Stand to one side of it and draw the pendulum weight towards you until it just touches the tip of your physicist’s nose. Now just let the pendulum weight go. Don’t give it any push. It will swing away from your nose and then return back towards the tip of your nose. Will you flinch? Should you flinch? The answers are, well, ‘Yes and no’.
fn2
fn1
Galileo thought it was true for all swings of the chandelier, no matter how far they went. In fact, that is not true. It is true to very high accuracy for oscillations of ‘small’ amplitude. This type of oscillation is known to scientists as ‘simple harmonic motion’. It describes the behaviour of almost every stable system in Nature after it is slightly perturbed from its equilibrium state.
fn2
The pendulum cannot swing back to a greater height than where it began from (unless someone hits it to give it more energy). In practice, the pendulum always loses a little of its energy overcoming air resistance and overcoming friction at the point of its support, and so it will never quite return to the same height that it began from. The physicist is actually quite safe – but will always flinch none the less.
64
A Bike with Square Wheels
The bicycle is just as good company as most husbands and, when it gets old and shabby, a woman can dispose of it and get a new one without shocking the entire community.
Ann Strong
If your bike’s like my bike it’s got circular wheels. You might just have one of them, but you’ve probably got two of them, but either way they are circular. However, you will probably be surprised to learn that it didn’t have to be like this. You can have a perfectly steady ride on a bike with square wheels, as long as you ride on the right type of surface.
The important feature of a rolling wheel for the cyclist is that you don’t keep jolting up and down as the bicycle moves forward. With circular wheels on a flat surface this is the case: the centre of the cyclist’s body moves forward in a straight line when the bicycle moves forward in a straight line without any slipping. Use square wheels on a flat surface and you are going to have a very uncomfortable up-and-down ride. But could there be a differently shaped road surface that results in a smooth ride when you are using square wheels? All we need to check is whether there is a shape that leads to a straight-line motion of the cyclist when he has square wheels.
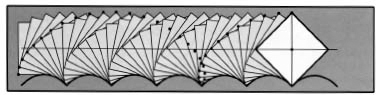
The answer is pretty surprising. The shape of the road surface that gives a steady ride on square wheels is created when you hang two ends of a chain from two points at the same height above ground. This is called the catenary and we have met it before in that connection in Chapter 11. If we turn it upside down we obtain the shape that is used for many of the great arches of the world. But if you take a catenary arch and repeat it over and over again along a line you get a sequence of undulations of the same height. This is the shape of the ground surface that gives us the smooth ride on square wheels. We just need the bottom corners of the square to fit into the sides of the successive ‘valleys’ on the surface. The key feature of the catenary is that when one is placed next to another, the angle between the two sides of the adjacent arches as they come into the lowest point of each valley is a right angle, 90 degrees, and that is the angle at each corner of the square. So, the right-angled wheel just keeps rolling along.
fn1
fn1
The square is not the only possible wheel shape that can give a smooth ride. Any polygonally-shaped wheel will work for a different catenary-shaped road. As the number of sides in the polygon gets very large, it begins to look more and more like a circle and the line of catenaries gets flatter and flatter and looks increasingly like a perfectly flat road. The case of a 3-sided polygon, a triangular wheel, is problematic because it runs into the side of the upcoming catenary before it can roll into the corner and hits the trailing side as it rolls out. You need to lay the road surface bit by bit to avoid these collisions happening. For a rolling polygonal wheel with N equal sides (so N = 4 is the case of our squared wheel), the equation of the catenary-shaped road that gives a smooth, straight-line rider for the cyclist is y = −B cosh(x/B), where B = C cot(π/N) with C constant.
65
How Many Guards Does an Art Gallery Need?
Who will guard the guards?
Juvenal
Imagine you are head of security at a large art gallery. You have many valuable paintings covering all of the gallery walls. They are also quite low on the walls, so that they can be viewed at eye level and so are vulnerable to theft or vandalism. The gallery is a collection of different rooms with different shapes and sizes. How are you going to make sure that each one of the pictures can be kept under surveillance all of the time. The solution is simple if you have unlimited money: just have one attendant standing on guard next to every picture. But art galleries are rarely awash with money, and wealthy donors don’t tend to earmark their gifts for the provision of guards and their chairs. So, in practice, you have a problem, a mathematical problem: what is the smallest number of attendants that you need to hire, and how should you position them so that all the walls of the gallery are visible at eye level?
We need to know the minimum number of guards needed to watch N walls. We assume that the walls are straight and a guard at a corner where two walls meet will be assumed to be able to see everything on those two walls, and we will assume that a
guard
’s view is never obstructed. A square gallery can obviously be watched by just one guard. In fact, if the gallery is shaped like any polygon in which all the sides bulge outwards (a ‘convex’ polygon) then one guard will always suffice.
Things get more interesting when the walls don’t all bulge outwards. Here is a gallery like that, with 8 walls, which can also be guarded by just one attendant located at the corner O.
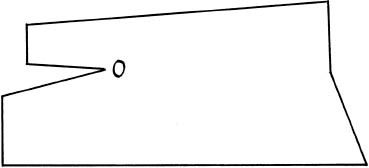
So, this is a rather economical gallery to run.
Here is another ‘kinkier’ 12-walled gallery that is not so efficient. It needs 4 guards to keep an eye on all the walls.
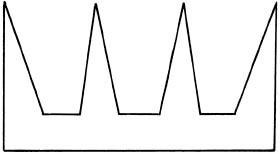
To solve the problem in general we just look at how we can divide the gallery up into triangles that don’t overlap. This can always be done. If the polygon has S vertices, then there will be S-2 triangles. Since a triangle is one of those convex shapes (the three-sided one) that needs only a single guard we know that if the gallery can be completely covered by, say, T non-overlapping triangles then it can always be guarded by T attendants. It might, of course, be guarded by fewer. For instance, we can always divide a square into two triangles by joining opposite diagonals, but we don’t need two guards to watch the walls, one will do. In general, the total number of guards that might be necessary to guard a gallery with W walls is the whole number part of W/3. For our 12-sided comb-shaped gallery this maximum is 12/3 = 4, whereas for an 8-sided gallery it is 2. Unfortunately, determining whether you need to use the maximum is not so easy and is a so-called ‘hard’ computer problem (See
chapter 27
) for which the computing time can double each time you add another wall to the problem.
Most of the galleries you visit today will not have kinked, jagged wall plans like these examples. They will have walls that are all at right angles like this:
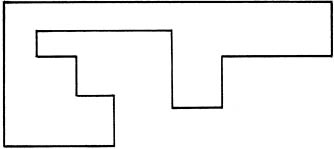
If there are many corners in a right-angled polygonal gallery like this, then the number of attendents located at the corners that
might
be necessary and is always sufficient to guard the gallery is the whole number part of ¼ × (Number of Corners). For the 14-cornered gallery shown here this number is 3. This means that it is much more economical on wages to have a gallery design like this, especially when it is large. If you have 150 walls, then the non-right-angled design could need 50 guards, while the right-angled set-up will need at most 37.
