Warped Passages (8 page)

Although the curled-up dimension of the Kaluza-Klein universe is not far away, it’s so small that any variation within it is imperceptible. Just as differences among New Yorkers don’t really matter to people outside, the structure in the extra dimensions of the universe is irrelevant when its details vary on such minuscule a scale. Even if fundamentally there turn out to be many more dimensions than we acknowledge in our daily lives, everything we see can still be described in terms of only the dimensions we observe. Extremely small extra dimensions change nothing about the way we view the world, or even about how we do most physics calculations. Even if additional dimensions exist, if we are incapable of seeing or experiencing them, we can ignore them and still correctly describe what we see. Later on
we’ll see modifications to this simple picture for which this won’t always be true, but those will involve additional assumptions.
We can understand one further important point about a rolled-up dimension from Figure 17, which illustrates the hose, or universe with one dimension, rolled up into a circle. Focus on any point along the infinite dimension. Notice that at each and every point there sits the entire compact space, namely the circle. The hose consists of all these circles glued together, like the slices I talked about in Chapter 1.
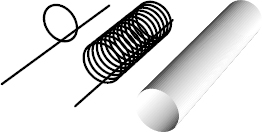
Figure 17.
In a two-dimensional universe, when a dimension is curled up there is a circle at every point along the infinite dimension of space.
Figure 18 presents a different example: here there are two infinite dimensions rather than one, plus a single additional dimension curled up into a circle. In this case, there is a circle at each and every
point in the two-dimensional space. And if there were three infinite dimensions, the rolled-up dimensions would exist at every point in three-dimensional space. You might liken the points in extra-dimensional space to the cells in your body, each of which carries your entire DNA sequence. Similarly, each point in our three-dimensional space could host an entire compactified circle.
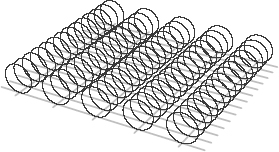
Figure 18.
In a three-dimensional universe, if one of the three dimensions is curled up you have a circle at every point in the plane.
So far, we’ve only considered a single additional dimension, which is rolled up into a circle. But everything we’ve said would hold true even if that curled-up dimension took some other shape—any shape at all. And it would also be true if there were two or more tiny, rolled-up dimensions of any shape at all. Any and all dimensions that are sufficiently small would be completely invisible to us.
Let us consider an example with two rolled-up dimensions. There are many possible shapes that these rolled-up dimensions could take. We’ll choose a
torus
, a donut-like shape in which the two additional dimensions are both simultaneously rolled into a circle. This is illustrated in Figure 19. If both circles—the one that winds through the donut hole and the one that winds around the donut itself—are sufficiently small, the additional two rolled-up dimensions would never be seen.

Figure 19.
When two out of four dimensions are curled into a donut, you have a donut at every point in space.
But that’s just one example. With more dimensions there are a huge number of conceivable
compact spaces
—spaces with rolled-up dimensions, distinguished by the precise manner in which the
dimensions are rolled up. One category of compact spaces important to string theory are the
Calabi-Yau manifolds
, named after the Italian mathematician Eugenio Calabi, who first proposed these particular shapes, and the Chinese-born Harvard mathematician Shing-Tung Yau, who showed that they are mathematically possible. These geometric shapes roll up and wind together extra dimensions in a very special way. The dimensions are curled up into a small size, as with all compactifications, but they are tangled in a way that is more complicated and difficult to draw.
4
Whatever shape the rolled-up extra dimensions take, and however many there are, at each point along the infinite dimensions there would be a small compact space containing all the curled-up dimensions. So, for example, if string theorists are right, everywhere in visible space—at the tip of your nose, at the North Pole of Venus, at the spot above the tennis court where your racket hit the ball the last time you served—there would be a six-dimensional Calabi-Yau manifold of invisibly tiny size. The higher-dimensional geometry would be present at every point in space.
String theorists often suggest—as Klein did—that curled-up dimensions are as small as the Planck length, 10
-33
cm. Planck-length-size compact dimensions would be extraordinarily well hidden; there is almost certainly no way for us to detect something so small. Therefore, Planck-length extra dimensions would very likely leave no visible trace of their existence. So even if we live in a universe with Planck-length extra dimensions, we would still register only the three familiar dimensions. The universe could have many such tiny dimensions, but we might never have the resolving power to find out.
Newton’s Gravitational Force Law with Extra Dimensions
It is nice to have a pictorial, descriptive explanation for why the extra dimensions are hidden when compactified, or rolled up, to a very minute size. But it’s a good idea to check that the laws of physics accord with this intuition.
Let’s take a look at Newton’s gravitational force law, the well-
established form of the gravitational force law that Newton proposed in the seventeenth century. This law tells us how the gravitational force depends on the distance between two massive objects.
*
It’s known as an
inverse square law
, which means that the strength of gravity decreases with distance proportionally to the distance squared. For example, if you double the distance between two objects, the strength of their gravitational attraction goes down by a factor of four. If the separation is increased to three times its original value, gravitational attraction decreases by a factor of nine. The inverse square law of gravity is one of the oldest and most important laws of physics. Among other things, it is the reason that planets have the type of orbits they do. Any viable physical theory of gravity must reproduce the inverse square law or it would be bound to fail.
The way in which the gravitational force law depends on distance, which is encoded in Newton’s inverse square law, is intimately connected to the number of spatial dimensions. This is because the number of dimensions determines how quickly gravity diffuses as it spreads out in space.
Let’s reflect on the connection, which will be very relevant to us later on when we consider extra dimensions. We’ll do this by imagining a water supply whose water can be directed through either a hose or a sprinkler. We’ll assume that both the hose and the sprinkler have the same amount of water running through them, and that they can each water a certain flower in a garden (see Figure 20). When the water goes through the hose, which is directed at the flower, the flower will get all the water. The distance from the base of the hose to the nozzle directed at the flower is irrelevant, because all the water must end up on the flower, no matter how far away the hose happened to be.
However, suppose instead that the same water is directed through a sprinkler that simultaneously waters many flowers. That is, the sprinkler sends out water in a circle, reaching all the flowers a certain distance away. Because the water will now be distributed among everything at that distance, the original flower will no longer get all
the water. Moreover, the farther away the flower is from the source, the more greenery the sprinkler will water, and the more widely distributed the water will be (see Figure 21). That’s because you can fit more plants on a circle three meters in circumference, say, than a circle just one meter in circumference. Because the water is more widely spread out, a farther away flower receives less water.
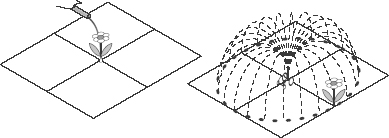
Figure 20.
The amount of water delivered to a flower by a sprinkler that sprinkles water around a circle is less than the amount delivered directly by a hose.
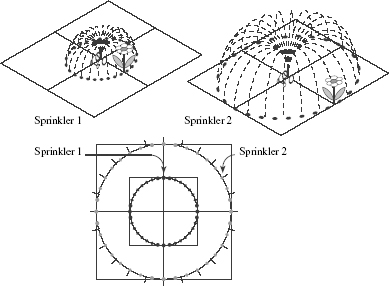
Figure 21.
When a sprinkler delivers water around a circle of larger radius, the water is spaced out more and the flower receives less water.
Similarly, anything that is shared uniformly in more than one direction will have a smaller impact on any particular thing that is farther away—whether that thing is a flower or, as we will soon see, an object experiencing the force of gravity. Gravity, like water, is more widely distributed when it is farther away.
With this example, we can also see why the distribution depends so strongly on the number of dimensions in which water (or gravity) is spread. The water from the two-dimensional sprinkler is spread out with distance, unlike the water from the one-dimensional hose, which is not spread out at all. Now imagine a sprinkler that spreads its water over the surface of a sphere, and not just around a circle. (Such a sprinkler would look something like a dandelion gone to seed.) Here, the water will spread out with distance much more quickly.
