Warped Passages (5 page)

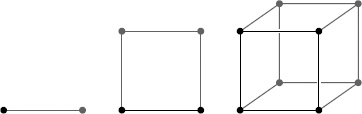
Figure 7.
How we put together lower-dimensional objects to make higher-dimensional ones. We connect two points to make a line segment, two line segments to make a square, two squares to make a cube, and (not pictured since it’s too difficult to draw) two cubes to make a hypercube.
We can generalize in four dimensions to a hypercube, and in five dimensions to something for which we don’t yet have a name. Even though we three-dimensional mortals have never seen these two objects, we can generalize the procedure that worked in lower dimensions. To construct a hypercube (also known as a tesseract), put one cube above the other, and connect them by adding six additional cubes, connecting the faces of the two original cubes. This construction is an abstraction and difficult to draw, but that doesn’t make the hypercube any less real.
In high school, I spent a summer at math camp (which was far more entertaining than you might think), where we were shown a film version of
Flatland
.
*
At the end, the narrator, in a delightful British accent, tried futilely to point to the third dimension that was inaccessible to Flatlanders, saying, “Upward, not Northward.” Unfortunately, we have the same frustration if we try to point to a fourth spatial
dimension, a passage. But just as Flatlanders didn’t see or travel through the third dimension, even though it existed in Abbott’s story, our not having yet seen another dimension doesn’t mean there is none. So although we haven’t yet observed or traveled through such a dimension, the subtext throughout
Warped Passages
will be, “Not Northward, but Forward along a passage.” Who knows what exists that we haven’t yet seen?
Three from Two
For the rest of this chapter, rather than thinking about spaces that have more than three dimensions, I will talk about how, with our limited visual capacity, we go about thinking and drawing three dimensions using two-dimensional images. Understanding how we perform this translation from two-dimensional images to three-dimensional reality will be useful later on when interpreting lower-dimensional “pictures” of higher-dimensional worlds. Think of this section as a warm-up exercise for wrapping your mind around extra dimensions. It might be good to remember that you cope with dimensionality all the time in ordinary life. It really isn’t that unfamiliar.
Often all we can see are parts of the surface of things, the surface being only the exterior. This exterior has two dimensions, even though it curves through three-dimensional space, because you only need two numbers to identify any point. We deduce that the surface isn’t three-dimensional because it has no thickness.
When we look at pictures, movies, computer screens, or the figures in this book, we are generally looking at two-dimensional, not three-dimensional representations. But we can nonetheless deduce the three-dimensional reality that is being portrayed.
We can use two-dimensional information to construct three dimensions. This involves suppressing information in making two-dimensional representations while trying to keep enough information to reproduce essential elements of the original object. Let’s now reflect on the methods we often use to reduce higher-dimensional objects to lower dimensions—slicing, projection, holography, and sometimes
just ignoring the dimension—and how we work backwards to deduce the three-dimensional objects they represent.
The least complicated way of seeing beyond the surface is to make slices. Each slice is two-dimensional, but the combination of the slices forms a real three-dimensional object. For example, when you order ham at the deli, the three-dimensional lump of ham is readily exchanged for many two-dimensional slices.
*
By stacking all the slices you could reconstruct the full three-dimensional shape.
This book is three-dimensional. However, its pages have only two dimensions. The union of the two-dimensional pages comprises the book.
†
We could illustrate this union of pages in many ways. One is shown in Figure 8, in which we view the book edge on. In this picture we’ve again played with dimensionality, since each line represents a page. So long as we all know that the lines represent two-dimensional pages, this illustration should be clear. Later on, we’ll use a similar shorthand when we depict objects in multidimensional worlds.
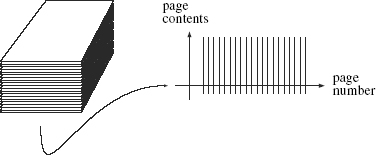
Figure 8.
A three-dimensional book is made up of two-dimensional pages.
Slicing is only one way to replace higher dimensions with lower
ones.
Projection
, a technical term borrowed from geometry, is another. A projection gives a definite prescription for creating a lower-dimensional representation of an object. A shadow on a wall is an example of a two-dimensional projection of a three-dimensional object. Figure 9 illustrates how information is lost when we (or rabbits) make a projection. Points on the shadow are identified by only two coordinates, left-right or up-down along the wall. But the object that is projected also has a third spatial dimension that the projection doesn’t retain.

Figure 9.
A projection carries less information than the higher-dimensional object.
The simplest way to make a projection is to just ignore one dimension. For example, Figure 10 shows a cube in three dimensions being projected onto two dimensions. The projections can take many forms, the simplest of which is a square.
To return to our earlier examples of the graphs of Ike and Athena, we might make a two-dimensional plot of Ike by neglecting his driving fast cars. And we might not really want to know the number of owls Athena raises, and might therefore make a four-dimensional rather than a five-dimensional plot. Disregarding Athena’s owls is a projection.
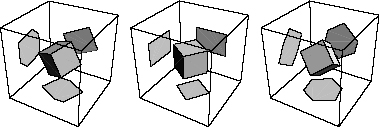
Figure 10.
Projections of a cube. Notice that the projection can be a square, as we see in the middle diagram, but that projections can also take other shapes.
A projection discards information from the original, higher-dimensional object (see Figure 9). However, when we make a lower-dimensional picture using a projection, we sometime include information to help retain some of what was lost. The additional information might be shading or color, as in a painting or photograph. It might be a number, as in a topographic map to illustrate height. Or there might be no label at all, in which case the two-dimensional characterization simply offers less information.
Without both our eyes, which work together to let us reconstruct three dimensions, everything we see would be projections. Depth perception is tougher when you close one of your eyes. A single eye constructs a two-dimensional projection of three-dimensional reality. You need two eyes to reproduce three dimensions.
I am nearsighted in one eye and farsighted in the other, so I don’t properly combine the images from both eyes unless I’m wearing glasses—which is rarely the case. Although I was told I should have trouble reconstructing three dimensions, I don’t usually notice any problem: things still look three-dimensional to me. That is because I rely on shading and perspective (and my familiarity with the world) to reconstruct three-dimensional images.
But one day in the desert, a friend and I were trying to reach a distant cliff. My friend kept telling me that we could walk directly there, and I couldn’t understand why he was insisting that we should walk straight through a piece of rock. It turned out the rock that I thought projected directly from the cliff, so that it would completely block our way, was in fact located much closer to us, in front of the
cliff. The rock I had thought would bar our path wasn’t actually attached to the cliff at all. This misunderstanding occurred because we were near the cliff around noon, when there were no shadows, and I had no way to construct the third dimension that would have told me how the distant cliffs and rocks were lined up. I wasn’t really conscious of my compensating strategy of using shading and perspective until then, when it failed.
Painting and drawing have always required artists to reduce what they see to projected images. Medieval art did this in the simplest manner. Figure 11 shows a mosaic image of a city as a two-dimensional projection. This mosaic doesn’t tell us anything about a third dimension; there are no labels or indications of its existence.
Since medieval times, painters have developed ways to make projections that partially redress painting’s loss of a dimension. One approach that opposes the medieval flattening of space is the method used by the cubists in the twentieth century. A cubist painting (for example Picasso’s
Portrait of Dora Maar
, Figure 12) presents several projections simultaneously, each from a different angle, and thereby conveys the subject’s three-dimensionality.
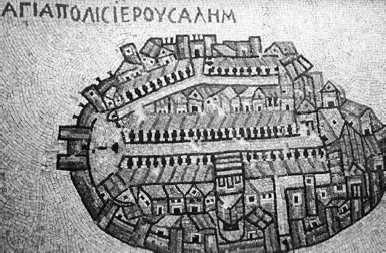
Figure 11.
A two-dimensional medieval mosaic.

