The Source Field Investigations (51 page)

In November 2010, Prince Charles released his new book
Harmony: A New Way of Looking at Our World—
in which he uses Martineau’s groundbreaking research to argue that the Universe displays evidence of a “grammar of harmony.”

Kepler’s vision of the planets is first discussed on page 12 of Martineau’s book.

On page 14, things get much more interesting: “Kepler . . . particularly noticed that the ratios between planets’ extreme angular velocities were all harmonic intervals.” Then, Martineau begins delivering the goods.

Absolutely yes. The five-sided pentagon is found in both the dodecahedron, with its five-sided faces, and the icosahedron, with groups of five triangles sharing common points—so we’re definitely on to something.

On page 20, Martineau makes the intriguing suggestion that even though the planetary orbits are elliptical, we can still study the basic proportions that hold them in place as if they were spherical. This is probably because their naturally spherical energy fields are being squeezed by the pressure and momentum of their movement through clouds of gas and dust in the galaxy.

I was stunned to see that if you draw one circle for the average orbit of Mercury, and put three of these circles together to make a triangle, then when you draw a circle around them, you get the orbit of Venus—within 99.9 percent. Of course, since these are actually spheres, it’s not a triangle at all—it’s our classic three-sided tetrahedron, the simplest of all the Platonic solids.

Then, on page 24, Martineau produces a remarkable geometric diagram of the relationship between Earth, Venus and the Sun. Every eight Earth years, or thirteen Venusian years, they line up to form the next corner of a perfect pentagon—with 99.9 percent precision. Even better, when we work in the nearest and farthest points Venus reaches during this eight-year dance, another pentagon is formed that is even larger—and in perfect proportion to the others. This very likely is the result of Platonic geometries within spheres of energy that are precisely structuring where the planets travel—again, in this case, thanks to the dodecahedron and icosahedron with their five-sided symmetry.

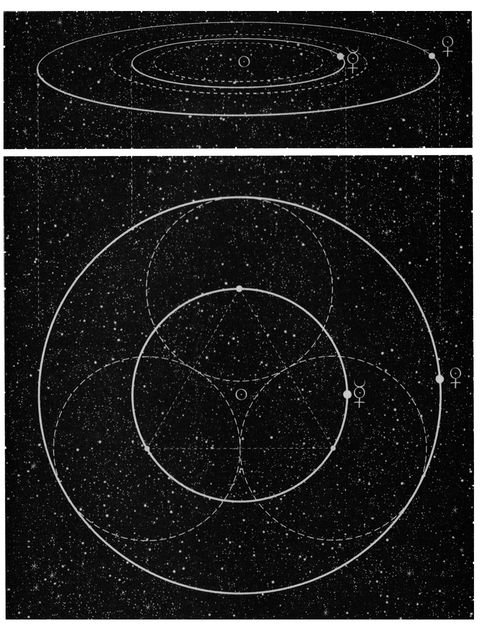
John Martineau illustrates a perfect triangular relationship between the orbits of Mercury and Venus. This triangle forms a tetrahedron in three dimensions.

On page 32, we find out that there is geometric precision between earth and the Moon—thanks to the work of Robin Heath. There are between twelve and thirteen full moons in a year. If we then draw a circle (again, a sphere) with a diameter of thirteen units, and inscribe a perfect, five-sided star inside it, each arm of the star will measure 12.364 units. This is the exact number of full moons in a year—to a 99.95-percent level of accuracy. This again suggests there is a sphere of force between earth and the Moon—where the Moon’s movements are being precisely driven by the rotating vortex currents of gravity within the dodecahedron geometry, which is all based on five-fold symmetry.

I was amazed when I saw pages 34 and 35, as Martineau shows that the relationships between the spacing of Venus, Earth and Mars are all perfectly defined by the icosahedron and dodecahedron. In this case, Martineau directly names and illustrates these two geometries. Mars is obviously the farthest away of these three planets, and if you make that orbit into a perfect sphere, you can then put the sphere of Venus’s orbit inside of it. The distance between the sphere of Venus and the sphere of Mars is precisely defined by the dodecahedron—with 99.98-percent perfection. Then, if you flip this same dodecahedron inside out to get the icosahedron, you can fit a larger sphere inside of it—and that happens to be the exact distance of Earth’s orbit, within 99.9-percent accuracy. If the details seem confusing, you can go read the book and get into all the specifics—but these are very clear geometric relationships between the planets, just like the geometry we see in quantum mechanics and the global grid.

The magic continues to happen as we go farther out. When we draw a circle for the orbit of Mars, we can then put it in the middle of a group of four larger circles that touch each other perfectly. Each of these four larger circles is precisely the size of Jupiter’s average orbit, with 99.98-percent perfection. This obviously forms a square, which becomes a cube—so there appears to be a hidden, cubical energy field between these two planets, determining the exact distance and timing of their orbits from each other. Martineau also shows a beautiful cubical relationship between Jupiter’s two largest moons, Ganymede and Callisto—and also reveals a perfect cubical relationship (within 99.9 percent) by comparing the orbit of Earth and Mars.

One of the biggest dead giveaways that there is geometry in the solar system is in the Trojans, which are clusters of asteroids that orbit in front of and behind Jupiter in the same loop. One cluster is always precisely sixty degrees ahead of Jupiter, and the other cluster is always sixty degrees behind Jupiter. There has never been a compelling scientific explanation of why this is happening. Obviously, this sixty-degree spacing allows you to start drawing geometric patterns if you represent Jupiter’s orbit as a perfect sphere. I was stunned to see that if you take the sphere of Jupiter’s orbit and nest three cubes, three octahedrons or any other combination of these two shapes together, one inside the other, you get a sphere in the center that is exactly the size of earth’s orbit—with 99.8 percent perfection.

Then, Jupiter and Saturn have a very close five-to-two relationship between their orbital periods. They make a conjunction every twenty years, but each conjunction appears at a new point within the great circle of their shared orbits. If you plot out six of these conjunctions within that shared circle and connect the dots, you get a perfect Star of David. This is the geometry of the star tetrahedron or merkabah—where you have one tetrahedron pointing up and another one pointing down, blended together. Again, the Platonic solids are working their magic.

Lastly, on pages 48 and 49, we find another triangle, or tetrahedron, in the relationship between the orbit of Uranus and Saturn. I was also intrigued that the radius of Saturn’s orbit is equal to the circumference of Mars’s orbit, to 99.9-percent accuracy—and the circumference of Saturn’s orbit is the same as the diameter of Neptune’s orbit. Just so Pluto doesn’t feel left out, we discover on page 50 that “Neptune’s orbital period is twice that of Uranus, and Uranus’s is two-thirds that of Pluto.” That means our entire solar system is being governed by a series of absolutely perfect geometric relationships, many of which can be directly associated with the Platonic solids. As Prince Charles said, “This may, of course, all be a coincidence, but such is their precision it does begin to challenge the popular notion that we live in an accidental universe. . . .”
⁵

I was absolutely stunned. I had felt for fifteen years that this must be the answer, but other books I’d read on sacred geometry seemed to suggest that Kepler’s dream was ultimately a failure. Now I realized they simply hadn’t worked hard enough to see the truth—but John Martineau had done his homework and figured everything out. I did already know that galaxies gathered into massive superclusters, and those superclusters mysteriously arrange into gigantic, diamond-shaped octahedrons.
⁶
The octahedrons form a matrix—repeating over and over again across vast distances.
^7
-
8
-
9

The background dust and gas at the farthest reaches of the Universe also clusters into the shape of an octahedron.
¹⁰
Further analysis revealed a dodecahedron pattern in the dust as well.
¹¹
These laws truly do extend throughout the entire Universe, at all levels of size.

If you’re scratching your head at this point and wondering why I even bothered to mention all this, let me make myself clear. We’ve already seen evidence that Sanderson’s twelve main vortex points create direct gateways into time-space. A huge number of ships and planes have seen strange lights appear in the sea or in the sky, had bizarre equipment malfunctions, spontaneously moved forward or backward in time, warped through space from one place to another, or simply dematerialized entirely—making a complete crossover into time-space. The key, as the ancients obviously knew, is in the geometry. Or, as the old saying goes, “X marks the spot.”

I now had the proof that these same three-dimensional geometric relationships existed in the planetary orbits. This meant planetary conjunctions were much more interesting than just dates on a calendar. During these alignments, gigantic interplanetary geometry is lining up as well—creating greater coherence here on earth as all that energy multiplies. The more of an alignment you have between these hidden geometric energy patterns in the solar system, the more coherence you have—and the more likely you are to be able to directly travel through time-space.

The ancients may have been very aware that at certain times, a particular geometric node on earth would come into alignment with other geometry in the solar system—and this is when the magic happens. Then, if you’ve built a pyramid, or even a stone circle, you can generate even more coherence—as we saw with the Russian pyramid experiments. (Don’t forget that when the Russians charged rocks in the pyramid, and then arranged them around a growing crop, they got much more coherence in the area inside the rocks. So if you charged up the rocks that made Stonehenge, you now would get the same effect. And even if you didn’t charge them up first, simply arranging them in a circle should be enough to harness and concentrate the earth’s energy—by creating a circular vortex pattern.) I’ve also heard from insider sources that these alignments are the secret to alchemy. Lead will turn into gold in certain methods, but you have to know when to do it. Only when the earth and solar system produces the proper coherence will this ancient science of
Al-Kemit
—literally “the Science of Egypt”—actually work.

The Maya were obviously a pyramid-building culture, or at least inherited all their traditions from a pyramid-building culture. I do not believe that human sacrifice had anything to do with the original founding of the Maya civilization—this represented the end result of a long period of decay, moving ever-increasingly farther away from where it once started. It may well be that the ancient founders of the Maya civilization were, in fact, aware that you could levitate large stone blocks, teleport through space, and even travel through time when the geometry of the earth lined up with the geometry of the solar system. It is very likely that one of the main reasons they built the pyramids was to have a coherence generator—so that when these special alignments opened up, they could harness them. Obviously, if this were true, they would be very interested in tracking the orbits of the planets—with great precision.

I’ve seen many, many skeptics stridently attack the Maya calendar as if it were a bunch of meaningless nonsense. And even when people write about it in a favorable way, suggesting that the end date of 2012 is truly a significant event, hardly anyone actually crunches the numbers within the calendar to see if they mean something. More specifically, why were the Maya counting all these different cycles that mesh together with each other so perfectly? Why not just count earth days, lunar months and earth years, and leave it at that? I suspected that if I actually did the homework, I might find that the Maya were counting these cycles for a reason—and I struck gold.