The Singularity Is Near: When Humans Transcend Biology (22 page)

Watts’s own group has created functionally equivalent re-creations of these brain regions derived from reverse engineering. He estimates that 10
¹¹
cps are required to achieve human-level localization of sounds. The auditory cortex regions responsible for this processing comprise at least 0.1 percent of the brain’s neurons. So we again arrive at a ballpark estimate of around 10
¹⁴
cps (10
¹¹
cps × 10
³
).

Yet another estimate comes from a simulation at the University of Texas that represents the functionality of a cerebellum region containing 10
⁴
neurons; this required about 10
⁸
cps, or about 10
⁴
cps per neuron. Extrapolating this over an estimated 10
¹¹
neurons results in a figure of about 10
¹⁵
cps for the entire brain.

We will discuss the state of human-brain reverse engineering later, but it is clear that we can emulate the functionality of brain regions with less computation than would be required to simulate the precise nonlinear operation of each neuron and all of the neural components (that is, all of the complex interactions that take place inside each neuron). We come to the same conclusion when we attempt to simulate the functionality of organs in the body. For example, implantable devices are being tested that simulate the functionality of the human pancreas in regulating insulin levels.
⁴⁰
These devices work by measuring glucose levels in the blood and releasing insulin in a controlled fashion to keep the levels in an appropriate range. While they follow a method similar to that of a biological pancreas, they do not, however, attempt to simulate
each
pancreatic islet cell, and there would be no reason to do so.

These estimates all result in comparable orders of magnitude (10
¹⁴
to 10
¹⁵
cps). Given the early stage of human-brain reverse engineering, I will use a more conservative figure of 10
¹⁶
cps for our subsequent discussions.

Functional simulation of the brain is sufficient to re-create human powers of pattern recognition, intellect, and emotional intelligence. On the other hand, if we want to “upload” a particular person’s personality (that is, capture all of his or her knowledge, skills, and personality, a concept I will explore in greater detail at the end of
chapter 4
), then we may need to simulate neural processes at the level of individual neurons and portions of neurons, such as the soma (cell body), axon (output connection), dendrites (trees of incoming connections), and synapses (regions connecting axons and dendrites). For this, we need to look at detailed models of individual neurons. The “fan out” (number of interneuronal connections) per neuron is estimated at 10
³
. With an estimated 10
¹¹
neurons, that’s about 10
¹⁴
connections. With a reset time of five milliseconds, that comes to about 10
¹⁶
synaptic transactions per second.

Neuron-model simulations indicate the need for about 10
³
calculations per synaptic transaction to capture the nonlinearities (complex interactions) in the
dendrites and other neuron regions, resulting in an overall estimate of about 10
¹⁹
cps for simulating the human brain at this level.
⁴¹
We can therefore consider this an upper bound, but 10
¹⁴
to 10
¹⁶
cps to achieve functional equivalence of all brain regions is likely to be sufficient.

IBM’s Blue Gene/L supercomputer, now being built and scheduled to be completed around the time of the publication of this book, is projected to provide 360 trillion calculations per second (3.6 × 10
¹⁴
cps).
⁴²
This figure is already greater than the lower estimates described above. Blue Gene/L will also have around one hundred terabytes (about 10
¹⁵
bits) of main storage, more than our memory estimate for functional emulation of the human brain (see below). In line with my earlier predictions, supercomputers will achieve my more conservative estimate of 10
¹⁶
cps for functional human-brain emulation by early in the next decade (see the “Supercomputer Power” figure on
p. 71
).

Accelerating the Availability of Human-Level Personal Computing.
Personal computers today provide more than 10
⁹
cps. According to the projections in the “Exponential Growth of Computing” chart (
p. 70
), we will achieve 10
¹⁶
cps by 2025. However, there are several ways this timeline can be accelerated. Rather than using general-purpose processors, one can use application-specific integrated circuits (ASICs) to provide greater price-performance for very repetitive calculations. Such circuits already provide extremely high computational throughput for the repetitive calculations used in generating moving images in video games. ASICs can increase price-performance a thousandfold, cutting about eight years off the 2025 date. The varied programs that a simulation of the human brain will comprise will also include a great deal of repetition and thus will be amenable to ASIC implementation. The cerebellum, for example, repeats a basic wiring pattern billions of times.

We will also be able to amplify the power of personal computers by harvesting the unused computation power of devices on the Internet. New communication paradigms such as “mesh” computing contemplate treating every device in the network as a node rather than just a “spoke.”
⁴³
In other words, instead of devices (such as personal computers and PDAs) merely sending information to and from nodes, each device will act as a node itself, sending information to and receiving information from every other device. That will create very robust, self-organizing communication networks. It will also make it easier for computers and other devices to tap unused CPU cycles of the devices in their region of the mesh.

Currently at least 99 percent, if not 99.9 percent, of the computational capacity of all the computers on the Internet lies unused. Effectively harnessing this computation can provide another factor of 10
²
or 10
³
in increased
price-performance. For these reasons, it is reasonable to expect human brain capacity, at least in terms of hardware computational capacity, for one thousand dollars by around 2020.

Yet another approach to accelerate the availability of human-level computation in a personal computer is to use transistors in their native “analog” mode. Many of the processes in the human brain are analog, not digital. Although we can emulate analog processes to any desired degree of accuracy with digital computation, we lose several orders of magnitude of efficiency in doing so. A single transistor can multiply two values represented as analog levels; doing so with digital circuits requires thousands of transistors. California Institute of Technology’s Carver Mead has been pioneering this concept.
⁴⁴
One disadvantage of Mead’s approach is that the engineering design time required for such native analog computing is lengthy, so most researchers developing software to emulate regions of the brain usually prefer the rapid turnaround of software simulations.

Human Memory Capacity.
How does computational capacity compare to human memory capacity? It turns out that we arrive at similar time-frame estimates if we look at human memory requirements. The number of “chunks” of knowledge mastered by an expert in a domain is approximately 10
⁵
for a variety of domains. These chunks represent patterns (such as faces) as well as specific knowledge. For example, a world-class chess master is estimated to have mastered about 100,000 board positions. Shakespeare used 29,000 words but close to 100,000 meanings of those words. Development of expert systems in medicine indicate that humans can master about 100,000 concepts in a domain. If we estimate that this “professional” knowledge represents as little as 1 percent of the overall pattern and knowledge store of a human, we arrive at an estimate of 10
⁷
chunks.

Based on my own experience in designing systems that can store similar chunks of knowledge in either rule-based expert systems or self-organizing pattern-recognition systems, a reasonable estimate is about 10
⁶
bits per chunk (pattern or item of knowledge), for a total capacity of 10
¹³
(10 trillion) bits for a human’s functional memory.

According to the projections from the ITRS road map (see RAM chart on
p. 57
), we will be able to purchase 10
¹³
bits of memory for one thousand dollars by around 2018. Keep in mind that this memory will be millions of times faster than the electrochemical memory process used in the human brain and thus will be far more effective.

Again, if we model human memory on the level of individual interneuronal
connections, we get a higher estimate. We can estimate about 10
⁴
bits per connection to store the connection patterns and neurotransmitter concentrations. With an estimated 10
¹⁴
connections, that comes to 10
¹⁸
(a billion billion) bits.

Based on the above analyses, it is reasonable to expect the hardware that can emulate human-brain functionality to be available for approximately one thousand dollars by around 2020. As we will discuss in
chapter 4
, the software that will replicate that functionality will take about a decade longer. However, the exponential growth of the price-performance, capacity, and speed of our hardware technology will continue during that period, so by 2030 it will take a village of human brains (around one thousand) to match a thousand dollars’ worth of computing. By 2050, one thousand dollars of computing will exceed the processing power of all human brains on Earth. Of course, this figure includes those brains still using only biological neurons.

While human neurons are wondrous creations, we wouldn’t (and don’t) design computing circuits using the same slow methods. Despite the ingenuity of the designs evolved through natural selection, they are many orders of magnitude less capable than what we will be able to engineer. As we reverse engineer our bodies and brains, we will be in a position to create comparable systems that are far more durable and that operate thousands to millions of times faster than our naturally evolved systems. Our electronic circuits are already more than one million times faster than a neuron’s electrochemical processes, and this speed is continuing to accelerate.

Most of the complexity of a human neuron is devoted to maintaining its life-support functions, not its information-processing capabilities. Ultimately, we will be able to port our mental processes to a more suitable computational substrate. Then our minds won’t have to stay so small.

The Limits of Computation

If a most efficient supercomputer works all day to compute a weather simulation problem, what is the minimum amount of energy that must be dissipated according to the laws of physics? The answer is actually very simple to calculate, since it is unrelated to the amount of computation. The answer is always equal to zero.

                   —E
DWARD
F
REDKIN, PHYSICIST
⁴⁵

We’ve already had five paradigms (electromechanical calculators, relay-based computing, vacuum tubes, discrete transistors, and integrated circuits) that
have provided exponential growth to the price-performance and capabilities of computation. Each time a paradigm reached its limits, another paradigm took its place. We can already see the outlines of the sixth paradigm, which will bring computing into the molecular third dimension. Because computation underlies the foundations of everything we care about, from the economy to human intellect and creativity, we might well wonder: are there ultimate limits to the capacity of matter and energy to perform computation? If so, what are these limits, and how long will it take to reach them?

Our human intelligence is based on computational processes that we are learning to understand. We will ultimately multiply our intellectual powers by applying and extending the methods of human intelligence using the vastly greater capacity of nonbiological computation. So to consider the ultimate limits of computation is really to ask: what is the destiny of our civilization?

A common challenge to the ideas presented in this book is that these exponential trends must reach a limit, as exponential trends commonly do. When a species happens upon a new habitat, as in the famous example of rabbits in Australia, its numbers grow exponentially for a while. But it eventually reaches the limits of that environment’s ability to support it. Surely the processing of information must have similar constraints. It turns out that, yes, there are limits to computation based on the laws of physics. But these still allow for a continuation of exponential growth until nonbiological intelligence is trillions of trillions of times more powerful than all of human civilization today, contemporary computers included.

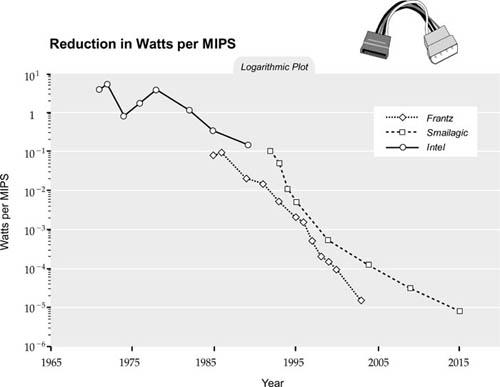
A major factor in considering computational limits is the energy requirement. The energy required per MIPS for computing devices has been falling exponentially, as shown in the following figure.
⁴⁶