Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (58 page)

(16)
(17)
(18)
(19)
(20)

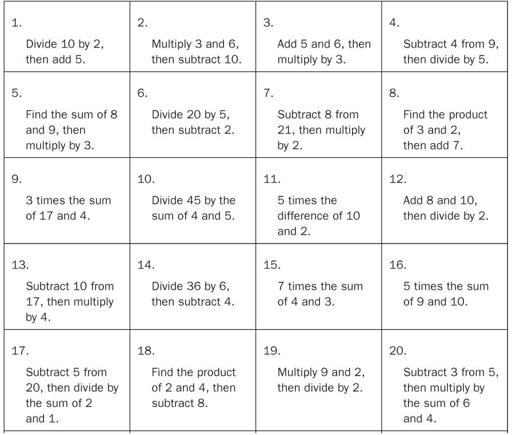
Expression Game Cards

Operations and Algebraic Thinking: 5.OA.3

“Analyze patterns and relationships.”

3. “Generate two numerical patterns using two given rules. Identify apparent relationships between corresponding terms. Form ordered pairs consisting of corresponding terms from the two patterns, and graph the ordered pairs on a coordinate plane.”

Background

When writing numerical patterns, students should first think of a rule, such as “start at 0 and add 4.” Then they may express the rule with numbers. The numbers generated by this rule are 0, 4, 8, 12, 16, . . . . Here is another rule: “Start at 0 and add 8.” This rule would result in the numbers 0, 8, 16, 24, 32, . . . .

These terms can be expressed as corresponding terms. They can be written as ordered pairs—(0, 0), (4, 8), (8, 16), (12, 24), (16, 32), and so on—and can be graphed in the coordinate plane. (See Geometry: 5.G.1 for instructions on constructing a coordinate plane.) When students look back to analyze these patterns, they should realize that the second number of each ordered pair in this example is twice the first number. This is because 8, which is twice as much as 4, is added in the second pattern.

Activity: Analyzing and Graphing Patterns

Working in pairs or groups of three, students will develop two numerical patterns. They will express the rule in words and numbers. They will then graph corresponding terms in the coordinate plane. The other students in class will analyze the patterns to determine the rule and relationship between the corresponding terms.

Materials

One sheet of transparent graph paper; one transparency; transparency marker for each pair or group of students; overhead projector.

Procedure

1.
Provide a few examples of patterns for your students. One example is 0, 5, 10, 15, 20, . . . . Ask students to find the rule, which is to start at 0 and add 5. Provide another pattern for your students, such as 0, 15, 30, 45, 60, . . . . Again, ask students to find the rule, which is to start at 0 and add 15. Ask your students to find a relationship between these two patterns. One relationship is that the terms in the second pattern are three times the corresponding terms in the first pattern.

2.
Model how to graph these ordered pairs in the coordinate plane. (See Geometry: 5.G.1.) Depending on the abilities of your students, you may need to review plotting points. Write ordered pairs formed by corresponding terms for the two patterns above. The ordered pairs are (0, 0), (5, 15), (10, 30), (15, 45), and (20, 60). Graph these ordered pairs.

3.
Explain that students will now work with their partner, or partners, and create numerical patterns. On a transparency, students will write two number patterns and ordered pairs formed by the corresponding terms of their patterns. On transparent graph paper, they will graph the ordered pairs. They should not write the rule in words for their pattern.

4.
When all pairs or groups have completed their patterns, ordered pairs, and graphs, have each show their work to the class on an overhead projector. The other students in class should express the pattern in words and find a numerical relationship between the two patterns.

Closure

Review any patterns that your students had difficulty with. Ask students to identify any patterns that have more than one rule.

Number and Operations in Base Ten: 5.NBT.1

“Understand the place value system.”

1. “Recognize that in a multi-digit number, a digit in one place represents 10 times as much as it represents in the place to its right and
of what it represents in the place to its left.”

Background

Our number system is based on powers of ten. Starting at the decimal point and moving left, the place values are ones, tens, hundreds, thousands, ten-thousands, hundred-thousands, millions, and so on. Moving right from the decimal point, the place values are tenths, hundredths, thousandths, ten-thousandths, hundred-thousandths, millionths, and so on.

Activity: What's My Number?

Working in groups of four or five, students will play a game—“What's My Number?”—in which they will write numbers when given clues about place value. Groups will compete against each other. The group with the highest point total at the end of the game is the winner.

Materials

Scissors; reproducibles, “Game Cards for Numbers, I” and “Game Cards for Numbers, II,” for each group of students.

Procedure

1.
Review place value with your students. It may be helpful to work as a class and make a place value chart as a visual representation.