Sex, Murder, and the Meaning of Life (26 page)
Read Sex, Murder, and the Meaning of Life Online
Authors: Douglas T. Kenrick

BOOK: Sex, Murder, and the Meaning of Life
8.77Mb size Format: txt, pdf, ePub
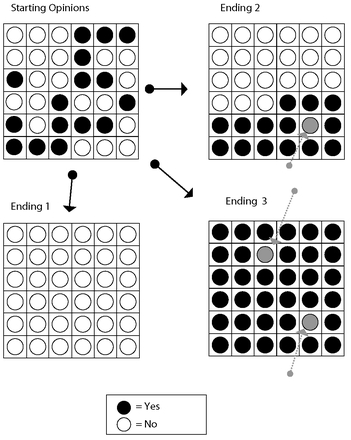
FIGURE 12.1
Self-organization in neighborhoods. The upper-left box depicts a neighborhood in which neighbors are split randomly on a particular issue. Assuming everyone wants to fit in with the majority of his or her neighbors, a few rounds of conversations between immediate neighbors will lead the neighborhood to become uniformly opposed. If one or two neighbors are committed to a favorable position (the grey individuals on the right), the final pattern may be profoundly different (as described in the text).
Self-organization in neighborhoods. The upper-left box depicts a neighborhood in which neighbors are split randomly on a particular issue. Assuming everyone wants to fit in with the majority of his or her neighbors, a few rounds of conversations between immediate neighbors will lead the neighborhood to become uniformly opposed. If one or two neighbors are committed to a favorable position (the grey individuals on the right), the final pattern may be profoundly different (as described in the text).
Think of the picture as a neighborhood, where the neighbors have to decide whether to vote yes or no on a plan for a special tax to build a new school. Let us assume that the initial distribution of opinions is mixed, and neighbors who are pro or con are randomly intermingled
with one another at the beginning. Assume also that people will talk to their immediate neighbors, and that they are motivated not to hold an unpopular opinion. After I set up a matrix like the one in
Figure 12.1
, I then had Excel update each individual's opinion to take into account the average of his or her immediate neighbors' original opinions.
with one another at the beginning. Assume also that people will talk to their immediate neighbors, and that they are motivated not to hold an unpopular opinion. After I set up a matrix like the one in
Figure 12.1
, I then had Excel update each individual's opinion to take into account the average of his or her immediate neighbors' original opinions.
So, after the first round of discussion, the person in the third house down on the left changed his opinion from yes to no, while some of his neighbors changed in the opposite direction. The final pattern was different depending on which random pattern I first plugged in. Nevertheless, after just a few rounds, the salt-and-pepper arrangements disappeared, and the neighborhood always ended up in a simpler, more uniform pattern. In this case, if everyone in the neighborhood simply attempted to bring his or her opinion in line with the majority, this neighborhood would have ended up being unanimously opposed, as in Ending 1 on the lower left.
Systems like this can start out very unstably, and small differences at the beginning can have a big effect on what the eventual equilibrium looks like. For example, Ending 2 (upper right) depicts what would happen if just one person (marked in gray) did not use a majority-rules criterion but instead leaned more strongly toward voting favorably. This person, let us called her Alberta, would change to a no only if her immediate neighbors were unanimously opposed; if even one favored yes on a given round of discussion, Alberta would stick with her yes. This single biased individual has a big effect in this case, so that the neighborhood eventually stabilizes into two camps in Ending 2âthe south camp favorable, and the north unfavorable. In the lower right picture (Ending 3), we see what would happen if there is only one more favorably biased person, let us call her Agnes (also marked in gray) in the north part of the neighborhood. Just these two people completely reversed the emergent neighborhood consensus.
Note that although the outcome was unstable at the beginning, it is very hard to change once the system has stabilized. If Agnes and Alberta were out of town when the first few rounds of discussion happened, the results would have stabilized as in Ending 1, and when Agnes and Alberta returned, they would have both gone along with what was now a unanimous neighborhood consensus against the idea. But after it stabilized favorably, as in Ending 3, unanimous support for the idea would persist even if they both later moved out of the neighborhood.
Where Do the Decision Biases Come From?In the simulation I showed you in
Figure 12.1
, the individual neighbors mostly used a simple decision rule: Match the majority of your neighbors. Biological anthropologists Rob Boyd, Pete Richerson, and Joe Henrich have gathered plenty of evidence that human beings are chock-full of conformity mechanisms, which usually serve us quite well (for example, you can randomly try out different leaves and roots for lunch and perhaps die experimenting, or you can eat the ones your neighbors are eating and survive). Psychologists Tanya Chartrand and John Bargh have found that our inclination to imitate other people is automatic and usually unconscious (if you are talking to someone who tends to shake her foot and scratch her eyebrow, you will start shaking your foot and scratching your eyebrow too, without even being aware of it). But as in the case of Agnes and Alberta, some people have higher or lower thresholds for letting others influence them.
Figure 12.1
, the individual neighbors mostly used a simple decision rule: Match the majority of your neighbors. Biological anthropologists Rob Boyd, Pete Richerson, and Joe Henrich have gathered plenty of evidence that human beings are chock-full of conformity mechanisms, which usually serve us quite well (for example, you can randomly try out different leaves and roots for lunch and perhaps die experimenting, or you can eat the ones your neighbors are eating and survive). Psychologists Tanya Chartrand and John Bargh have found that our inclination to imitate other people is automatic and usually unconscious (if you are talking to someone who tends to shake her foot and scratch her eyebrow, you will start shaking your foot and scratching your eyebrow too, without even being aware of it). But as in the case of Agnes and Alberta, some people have higher or lower thresholds for letting others influence them.
In my example, I presumed that people did not have strong preexisting opinions about the outcome. For many of the important decisions that we make in our lives, though, we have strong built-in biases. What determines whether you are favorably disposed to go along with the group or to take an independent stand, to take a dangerous risk or
to choose a safe option, to say yes or to say no to an offer to have sex, to fight or to run away in a conflict? To answer those questions, it is critically important to join together the insights of evolutionary psychology with those of dynamical systems theory. As I discussed in earlier chapters, a person's decision biases are predictably different, depending on whether that person is a man or a woman, which stage of life history that person has reached, what his or her chronic mating strategy is, and which of his or her motivational subselves is currently in the driver's seat.
to choose a safe option, to say yes or to say no to an offer to have sex, to fight or to run away in a conflict? To answer those questions, it is critically important to join together the insights of evolutionary psychology with those of dynamical systems theory. As I discussed in earlier chapters, a person's decision biases are predictably different, depending on whether that person is a man or a woman, which stage of life history that person has reached, what his or her chronic mating strategy is, and which of his or her motivational subselves is currently in the driver's seat.
For example, we saw that men whose mating subself is activated are likely to go
against
group opinion, but that women in a mating frame of mind are more likely to go along
with
the group. On the other hand, both men and women conform to group consensus when they are feeling threatened and their night watchman subselves are in charge. Furthermore, our preferred behavioral choices are dynamically linked to the current social situation. If there are a lot of available women as opposed to available men on the horizon, both sexes will adjust their mating strategy, for example. And on a moment-to-moment basis, there is a dynamic connection between the current situation and a person's reaction, so that the brain may switch motivational drivers if what looked initially like a mating opportunity suddenly starts to look a fight.
against
group opinion, but that women in a mating frame of mind are more likely to go along
with
the group. On the other hand, both men and women conform to group consensus when they are feeling threatened and their night watchman subselves are in charge. Furthermore, our preferred behavioral choices are dynamically linked to the current social situation. If there are a lot of available women as opposed to available men on the horizon, both sexes will adjust their mating strategy, for example. And on a moment-to-moment basis, there is a dynamic connection between the current situation and a person's reaction, so that the brain may switch motivational drivers if what looked initially like a mating opportunity suddenly starts to look a fight.
There is a profoundly important point here. If you want to understand how social complexity arises among humans, you cannot just assume we are like interchangeable ants and that the outcome will depend on random general processes that apply equally to any dynamical system. You have to realize that the outcomes will be powerfully influenced by the particular decision biases that mark our species and that those decision biases are very different depending on which social domain we are currently considering. Finally, individual differences can have a tremendous impact on how it all comes down in the end. I am not merely saying that “things are complex” out there. I am
saying that, ironically, we can reduce the complexity by avoiding the tendency to oversimplify. When we combine the insights of dynamical systems theory with those of evolutionary psychology, we get a much richer and more complete understanding of the pattern of social life likely to emerge in the particular kinds of situations we humans create for ourselves. In the next section, I consider how this combination of evolutionary and dynamic ideas yields some important insights, exploring how the different evolved biases inside our heads influence the very shape and structure of our social networks.
Emergent Social Geometriessaying that, ironically, we can reduce the complexity by avoiding the tendency to oversimplify. When we combine the insights of dynamical systems theory with those of evolutionary psychology, we get a much richer and more complete understanding of the pattern of social life likely to emerge in the particular kinds of situations we humans create for ourselves. In the next section, I consider how this combination of evolutionary and dynamic ideas yields some important insights, exploring how the different evolved biases inside our heads influence the very shape and structure of our social networks.
Although our social networks sometimes look like the flat square neighborhood in
Figure 12.1
, that is not always the case. In fact, there are different social geometries associated with the different fundamental motivations, as depicted in
Figure 12.2
. When it comes to status, for example, the geometry is inherently pyramidal, because there are fewer positions available as one goes higher up in the hierarchy. As I have already noted, status has double-barreled payoffs for men, affecting not only their direct access to goodies but also their chances of attracting a desirable mate. For this reason, men are more drawn into these sorts of competitive pyramidal arenas.
Figure 12.1
, that is not always the case. In fact, there are different social geometries associated with the different fundamental motivations, as depicted in
Figure 12.2
. When it comes to status, for example, the geometry is inherently pyramidal, because there are fewer positions available as one goes higher up in the hierarchy. As I have already noted, status has double-barreled payoffs for men, affecting not only their direct access to goodies but also their chances of attracting a desirable mate. For this reason, men are more drawn into these sorts of competitive pyramidal arenas.
The geometry for friendship networks, on the other hand, is flat and relatively permeable: If you are a friend of my brother, then you (and your brother) are likely to be a friend of mine. Females are, in general, more cooperative, and both sexes tend to prefer woman over men as friends. And although it is nice to have friends, truly close friendship networks are inherently limited by our finite budgets of time and energy. There are also coordination problems when the group gets too large: It is tough to throw a picnic if you have to worry about what two hundred people want to eat and drink (part of the reason big weddings are usually a lot more agony than ecstasy).
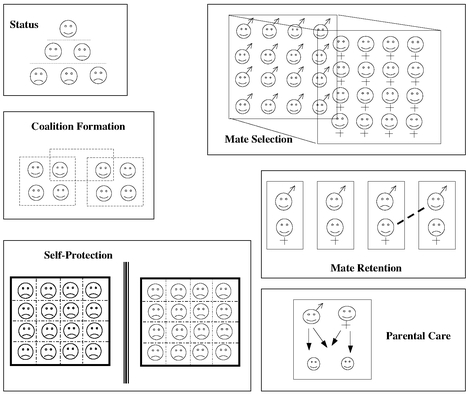
FIGURE 12.2
Emergent social geometries. Our social networks take very different forms depending on whom we are around and which of our subselves is currently in the driver's seat.
Emergent social geometries. Our social networks take very different forms depending on whom we are around and which of our subselves is currently in the driver's seat.
When we are worried about self-protection, though, the bigger the gang the better. During my period of hanging around with the hoodlums in the park, there was an actual “gang war” scheduled one night. One of the charming Italian kids from the Forty-sixth Street Boys had made a pass at the wrong guy's sister. The brother in question was a member of an actual Garrisons-style gang, complete with sweaters and jackets emblazoned “Chancellors.” Although gang wars had sounded cool when I was eight years old, I had seen that teenage boys could actually draw blood during conflicts and would have sooner been at home reading a book than setting myself up for a trip to the emergency room. But staying home on that particular night
would have brought no end of ridicule and harassment. So there I was, trying not to let my hands shake too much and trying in vain to suppress thoughts about what it would feel like to have a chain swung at my head or a knife stuck into my gut. Fortunately, though, every kid in the neighborhood and even some from nearby blocks had been recruited, so I could hope to stay on the periphery when the rumbling started.
would have brought no end of ridicule and harassment. So there I was, trying not to let my hands shake too much and trying in vain to suppress thoughts about what it would feel like to have a chain swung at my head or a knife stuck into my gut. Fortunately, though, every kid in the neighborhood and even some from nearby blocks had been recruited, so I could hope to stay on the periphery when the rumbling started.
As the gang of Chancellors rounded the corner, they were whooping and screaming, working themselves up into a war frenzy. There were a lot of them; we counted about fifty. But our group numbered closer to a hundred. The marauding Chancellors suddenly stopped dead in their tracks, and they must have made a quick visual calculation of the relative size of the two warring parties. After murmuring to one another for a minute or so, they turned around and ran in the other direction. According to Bert Hölldoebler and E. O. Wilson, ants, despite their inability to do arithmetic, have an emergent grouplevel ability to calculate relative group size, and like these teenage warriors, they are inclined to retreat from an intercolony battle when they discover that they are outnumbered.
Mate selection and mate retention have still different geometries. We select mates from a relatively large population, and are happiest when there are lots of alternatives from which to choose. When Norm Li, Jon Butner, and I surveyed men and women about their mating preferences, we found that the men were slightly more inclined toward promiscuity, whereas the women were strongly inclined toward monogamy. When we plugged men's and women's preferences into a series of dynamic simulations, we found that, over time, the women's preferences tended to win out, so that most simulated neighborhoods ended up predominantly monogamous, with self-perpetuating pockets of promiscuity at the edges. But we also found that the picture changed radically with only small shifts in the women's willingness to forgo monogamy (as you might find in a large city where there are
more women than men to go around). Under those circumstances, neighborhoods were more likely to stabilize into a pattern with larger pockets of promiscuity (as could be found in cities like Los Angeles and New York during the 1970s).
more women than men to go around). Under those circumstances, neighborhoods were more likely to stabilize into a pattern with larger pockets of promiscuity (as could be found in cities like Los Angeles and New York during the 1970s).
Relationship maintenance, on the other hand, is usually a twoperson game. Even in polygamous societies, most people end up in couples and not, like Bhupinder Singh, the immensely wealthy seventh maharaja of Patiala, with 350 partners.
If you have as few as two romantic partners, both of them are likely to regard that total as one too many, and each will probably try to drive the other one away. Even in societies with legal polygyny, wives fight with one another over access to the harem leader and over resources for their children. The reason that humans, unlike most other mammals, are so jealous is that both parents contribute resources to the offspring. The woman does not want the man's resources spread too thinly, and the man does not want to contribute resources to another man's child.
Other books
Kaleb by Nicole Edwards
Love Doesn't Work by Henning Koch
Call to Arms (War of the Fae: Book 2) by Casey, Elle
Truth or Dare by Peg Cochran
Gregory Maguire_Wicked Years_02 by Son of a Witch
The Faithless by Martina Cole
When Last I Died by Gladys Mitchell
The Wicked Wand by Steve Shilstone
