Panic in Level 4: Cannibals, Killer Viruses, and Other Journeys to the Edge of Science (8 page)

P
I WAS BY NO MEANS
the only unexplored number in the Chudnovskys’ inventory, but it was one that interested them. They wondered whether the digits contained a hidden rule, an as yet unseen architecture, close to the mind of God. A subtle and fantastic order might appear in the digits of pi way out there somewhere; no one knew. No one had ever proved, for example, that pi did not turn into a string of nines and zeros, spattered in some peculiar arrangement. It could be any sort of arrangement, just so long as it didn’t repeat periodically; for it has been proven that pi never repeats periodically. Pi could, however, conceivably start doing something like this: 122333444455555666666…. That is, the digits might suddenly shift into a strong pattern. Such a pattern is very regular, but it doesn’t repeat periodically. (Mathematicians felt it was very unlikely that pi would ever become obviously regular in some way, but no one had been able to prove that it
didn’t.
)

If we were to explore the digits of pi far enough, they might resolve into a breathtaking numerical pattern, as knotty as
The Book of Kells,
and it might mean something. It might be a small but interesting message from God, hidden in the crypt of the circle, awaiting notice by a mathematician. On the other hand, the digits of pi might ramble forever in a hideous cacophony, which was a kind of absolute perfection to a mathematician like Gregory Chudnovsky. Pi looked “monstrous” to him. “We know absolutely
nothing
about pi,” he declared from his bed. “What the hell does it mean? The definition of pi is really very simple—it’s just the circumference to the diameter—but the complexity of the sequence it spits out in digits is really unbelievable. We have a sequence of digits that looks like gibberish.”

“Maybe in the eyes of God pi looks perfect,” David said, standing in a corner of the bedroom, his head and shoulders visible above towers of paper.

Mathematicians call pi a transcendental number. In simple terms, a transcendental number is a number that exists but can’t be expressed in any finite series of finite operations.
^*2
For example, if you try to express pi as the solution to an algebraic equation made up of terms that have integer coefficients in them, you will find that the equation goes on forever. Expressed in digits, pi extends into the distance as far as the eye can see, and the digits don’t repeat periodically, as do the digits of a rational number. Pi slips away from all rational methods used to locate it. Pi is a transcendental number because it transcends the power of algebra to display it in its totality.

It turns out that
almost all
numbers are transcendental, yet
only a tiny handful
of them have ever actually been discovered by humans. In other words, humans don’t know anything about
almost all numbers.
There are certainly vast classes and categories of transcendental numbers that have never even been conjectured by humans—we can’t even imagine them. In fact, it’s very difficult even to prove that a number is transcendental. For a while, mathematicians strongly suspected that pi was a transcendental number, but they couldn’t prove it. Eventually, in 1882, a German mathematician named Ferdinand von Lindemann proved the transcendence of pi. He proved, in effect, that pi can’t be written on any piece of paper, no matter how big: a piece of paper as big as the universe would not even begin to be large enough to hold the tiniest droplet of pi. In a manner of speaking, pi is undescribable and cannot be found.

The earliest known reference to pi in human history occurs in a Middle Kingdom papyrus scroll, written around 1650
B.C.E
. by a scribe named Ahmes. He titled his scroll “The Entrance into the Knowledge of All Existing Things.” He led his readers through various mathematical problems and solutions, and toward the end of the scroll he found the area of a circle, using a rough sort of pi.

Around 200
B.C.E
., Archimedes of Syracuse found that pi is somewhere between 3
¹⁰
/71 and 3
¹
/7. That’s about 3.14. (The Greeks didn’t use decimals.) Archimedes had no special term for pi, calling it “the perimeter to the diameter.” By in effect approximating pi to two places after the decimal point, Archimedes narrowed down the suspected location of pi to one part in a hundred. After that, knowledge of pi bogged down. Finally, in the seventeenth century, a German mathematician named Ludolph van Ceulen approximated pi to thirty-five decimal places, or one part in a hundred million billion billion billion—a calculation that took Ludolph most of his life to accomplish. It gave him such satisfaction that he had the thirty-five digits of pi engraved on his tombstone, which ended up being installed in a special graveyard for professors in St. Peter’s Church in Leiden, in the Netherlands. Ludolph was so admired for his digits that pi came to be called the Ludolphian number. But then his tombstone vanished from the graveyard, and some people think it was turned into a sidewalk slab. If so, somewhere in Leiden people are probably walking over Ludolph’s digits. The Germans still call pi the Ludolphian number.

In the eighteenth century, Leonhard Euler, mathematician to Catherine the Great, empress of Russia, began calling it
p
or
c.
The first person to use the Greek letter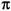
was William Jones, an English mathematician, who coined it in 1706. Jones probably meant
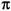to stand for “periphery.”

It is hard to ignore the ubiquity of pi in nature. Pi is obvious in the disks of the moon and the sun. The double helix of DNA revolves around pi. Pi hides in the rainbow and sits in the pupil of the eye, and when a raindrop falls into water, pi emerges in the spreading rings. Pi can be found in waves and spectra of all kinds, and therefore pi occurs in colors and music, in earthquakes, in surf. Pi is everywhere in superstrings, the hypothetical loops of energy that may vibrate in many dimensions, forming the essence of matter. Pi occurs naturally in tables of death, in what is known as a Gaussian distribution of deaths in a population. That is, when a person dies, the event “feels” the Ludolphian number.

It is one of the great mysteries why nature seems to know mathematics. No one can suggest why this should be so. Eugene Wigner, the physicist, once said that the miracle in the way the language of mathematics fits the laws of physics “is a wonderful gift which we neither understand nor deserve.” We may not understand or deserve pi, but nature is aware of it, as Captain O. C. Fox learned while he was recovering in a hospital from a wound that he got in the American Civil War. Having nothing better to do with his time than lie in bed and derive pi, Captain Fox spent a few weeks tossing pieces of fine steel wire onto a wooden board ruled with parallel lines. The wires fell randomly across the lines in such a way that pi emerged in the statistics. After throwing his wires on the floor eleven hundred times, Captain Fox was able to derive pi to two places after the decimal point—he got it to the same accuracy that Archimedes did. But Captain Fox’s method was not efficient. Each digit took far more time to get than the previous one. If he had had a thousand years to recover from his wound, he might have gotten pi to perhaps another decimal place. To go deeper into pi, it is necessary to use a machine.

The race toward pi happened in cyberspace, inside supercomputers. In the beginning, computer scientists used pi as an ultimate test of a machine. Pi is to a computer what the East Africa rally is to a car. In 1949, George Reitwiesner, at the Ballistic Research Laboratory, in Maryland, derived pi to 2,037 decimal places with the
ENIAC
, the first general-purpose electronic digital computer. Working at the same laboratory, John von Neumann (one of the inventors of the
ENIAC
), searched those digits for signs of order but found nothing he could put his finger on. A decade later, Daniel Shanks and John W. Wrench, Jr., approximated pi to a hundred thousand decimal places with an IBM 7090 mainframe computer, and saw nothing. This was the Shanks-Wrench pi, a milestone. The race continued in a desultory fashion. Eventually, in 1981, Yasumasa Kanada, the head of a team of computer scientists at Tokyo University, used an NEC supercomputer, a Japanese machine, to compute two million digits of pi. People were astonished that anyone would bother to do it, but that was only the beginning of the affair. In 1984, Kanada and his team got sixteen million digits of pi. They noticed nothing remarkable. A year later, William Gosper, a mathematician and distinguished hacker employed at Symbolics, Inc., in Sunnyvale, California, computed pi to seventeen and a half million places with a smallish workstation, beating Kanada’s team by a million-and-a-half digits. Gosper saw nothing of interest.

The next year, David H. Bailey, at NASA, used a Cray supercomputer and a formula discovered by two brothers, Jonathan and Peter Borwein, to scoop twenty-nine million digits of pi. Bailey found nothing unusual. A year after that, Kanada and his Tokyo team got 134 million digits of pi. They saw no patterns anywhere. Kanada stayed in to the game. He went past two hundred million digits, and saw further amounts of nothing. Then the Chudnovsky brothers (who had not previously been known to have any interest in calculating pi) suddenly announced that they had obtained 480 million digits of pi—a world record—using supercomputers at two sites in the United States. Kanada’s Tokyo team seemed to be taken by surprise. The emergence of the Chudnovskys as competitors sharpened the Tokyo team’s appetite for more pi. They got on a Hitachi supercomputer and ripped through 536 million digits of pi, beating the Chudnovsky brothers and setting a new world record. They saw nothing new in pi. The brothers responded by smashing through
one billion
digits. Kanada’s restless boys and their Hitachi were determined not to be beaten, and they soon pushed into
slightly more
than a billion digits. The Chudnovskys took up the challenge and squeaked past the Japanese team again, having computed pi to 1,130,160,664 decimal places, without finding anything special. It was another world record. At this point, the brothers gave up, out of boredom.

If a billion decimals of pi were printed in ordinary type, they would stretch from New York City to the middle of Kansas. This notion raises a question: What is the point of computing pi from New York to Kansas? That question was indeed asked among mathematicians, since an expansion of pi to only forty-seven decimal places would be sufficiently precise to inscribe a circle around the visible universe that doesn’t deviate from perfect circularity by more than the distance across a single proton. A billion decimals of pi go so far beyond that kind of precision, into such a lunacy of exactitude, that physicists will never need to use the quantity in any experiment—at least, not for any physics we know of today. The mere thought of a billion decimals of pi gave some mathematicians a feeling of indefinable horror, and they declared the Chudnoskys’ effort trivial.

I asked Gregory if an impression I had of mathematicians was true, that they spend a certain amount of time declaring one another’s work trivial. “It is true,” he admitted. “There is actually a reason for this. Because once you know the solution to a problem it usually is trivial.”

For that final, record-breaking, Hitachi-beating, transbillion-digit push into pi, Gregory did the calculation from his bed in New York, working on the Internet with the Cray supercomputer in Minneapolis, occasionally answering the phone when the system operator called to ask why the Cray had crashed. Gregory also did some of the pi work on a massive IBM dreadnought mainframe at the Thomas J. Watson Research Center, in Yorktown Heights, New York, where he also triggered some dramatic crashes. The calculation of more than a billion digits of pi took half a year. This was because the Chudnovsky brothers could get time on the supercomputers only in bits and pieces, usually during holidays and in the dead of night.