Hyperspace (9 page)
Authors: Michio Kaku,Robert O'Keefe

Riemann persisted with his work in physics. In 1858, he even announced that he had finally succeeded in a unified description of light and electricity. He wrote, “I am fully convinced that my theory is the correct one, and that in a few years it will be recognized as such.”
8
Although his metric tensor gave him a powerful way to describe any curved space in any dimension, he did not know the precise equations that the metric tensor obeyed; that is, he did not know what made the sheet crumple.
Unfortunately, Riemann’s efforts to solve this problem were continually thwarted by grinding poverty. His successes did not translate into money. He suffered another nervous breakdown in 1857. After many years, he was finally appointed to Gauss’s coveted position at Göttingen, but it was too late. A life of poverty had broken his health, and like many of the greatest mathematicians throughout history, he died prematurely of consumption at the age of 39, before he could complete his geometric theory of gravity and electricity and magnetism.
In summary, Riemann did much more than lay the foundation of the mathematics of hyperspace. In retrospect, we see that Riemann anticipated some of the major themes in modern physics. Specifically,
1. He used higher-dimensional space to simplify the laws of nature; that is, to him, electricity and magnetism as well as gravity were just effects caused by the crumpling or warping of hyperspace.
2. He anticipated the concept of wormholes. Riemann’s cuts are the simplest examples of multiply connected spaces.
3. He expressed gravity as a field. The metric tensor, because it describes the force of gravity (via curvature) at every point in space, is precisely Faraday’s field concept when applied to gravity.
Riemann was unable to complete his work on force fields because he lacked the field equations that electricity and magnetism and gravity obey. In other words, he did not know precisely how the universe would be crumpled in order to yield the force of gravity. He tried to discover the field equations for electricity and magnetism, but he died before he could finish that project. At his death, he still had no way of calculating how much crumpling would be necessary to describe the forces. These crucial developments would be left to Maxwell and Einstein.
The spell was finally broken.
Riemann, in his short life, lifted the spell cast by Euclid more than 2,000 years before. Riemann’s metric tensor was the weapon with which young mathematicians could defy the Boeotians, who howled at any mention of higher dimensions. Those who followed in Riemann’s footsteps found it easier to speak of unseen worlds.
Soon, research bloomed all over Europe. Prominent scientists began
popularizing the idea for the general public. Hermann von Helmholtz, perhaps the most famous German physicist of his generation, was deeply affected by Riemann’s work and wrote and spoke extensively to the general public about the mathematics of intelligent beings living on a ball or sphere.
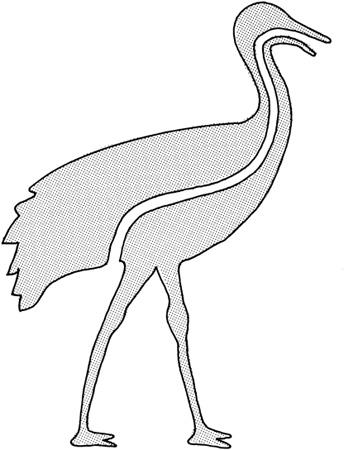
Figure 2.5. A two-dimensional being cannot eat. Its digestive tract necessarily divides it into two distinct pieces, and the being falls apart
.
According to Helmholtz, these creatures, with reasoning powers similar to our own, would independently discover that all of Euclid’s postulates
and theorems were useless. On a sphere, for example, the sums of the interior angles of a triangle do not add up to 180 degrees. The “bookworms” first talked about by Gauss now found themselves inhabiting Helmholtz’s two-dimensional spheres. Helmholtz wrote that “geometrical axioms must vary according to the kind of space inhabited by beings whose powers of reasoning are quite in conformity with ours.”
9
However, in his
Popular Lectures of Scientific Subjects
(1881), Helmholtz warned his readers that it is impossible for us to visualize the fourth dimension. In fact, he said “such a ‘representation’ is as impossible as the ‘representation’ of colours would be to one born blind.”
10
Some scientists, marveling at the elegance of Riemann’s work, tried to find physical applications for such a powerful apparatus.
11
While some scientists were exploring the applications of higher dimension, other scientists asked more practical, mundane questions, such as: How does a two-dimensional being eat? In order for Gauss’s two-dimensional people to eat, their mouths would have to face to the side. But if we now draw their digestive tract, we notice that this passageway completely bisects their bodies (
Figure 2.5
). Thus if they eat, their bodies will split into two pieces. In fact, any tube that connects two openings in their bodies will separate them into two unattached pieces. This presents us with a difficult choice. Either these people eat like we do and their bodies break apart, or they obey different laws of biology.
Unfortunately, the advanced mathematics of Riemann outstripped the relatively backward understanding of physics in the nineteenth century. There was no physical principle to guide further research. We would have to wait another century for the physicists to catch up with the mathematicians. But this did not stop nineteenth-century scientists from speculating endlessly about what beings from the fourth dimension would look like. Soon, they realized that such a fourth-dimensional being would have almost God-like powers.
Imagine being able to walk through walls.
You wouldn’t have to bother with opening doors; you could pass right through them. You wouldn’t have to go around buildings; you could enter them through their walls and pillars and out through the back wall. You wouldn’t have to detour around mountains; you could step right into them. When hungry, you could simply reach through the
refrigerator door without opening it. You could never be accidentally locked outside your car; you could simply step through the car door.
Imagine being able to disappear or reappear at will. Instead of driving to school or work, you would just vanish and rematerialize in your classroom or office. You wouldn’t need an airplane to visit far-away places, you could just vanish and rematerialize where you wanted. You would never be stuck in city traffic during rush hours; you and your car would simply disappear and rematerialize at your destination.
Imagine having x-ray eyes. You would be able to see accidents happening from a distance. After vanishing and rematerializing at the site of any accident, you could see exactly where the victims were, even if they were buried under debris.
Imagine being able to reach into an object without opening it. You could extract the sections from an orange without peeling or cutting it. You would be hailed as a master surgeon, with the ability to repair the internal organs of patients without ever cutting the skin, thereby greatly reducing pain and the risk of infection. You would simply reach into the person’s body, passing directly through the skin, and perform the delicate operation.
Imagine what a criminal could do with these powers. He could enter the most heavily guarded bank. He could see through the massive doors of the vault for the valuables and cash and reach inside and pull them out. He could then stroll outside as the bullets from the guards passed right through him. With these powers, no prison could hold a criminal.
No secrets could be kept from us. No treasures could be hidden from us. No obstructions could stop us. We would truly be miracle workers, performing feats beyond the comprehension of mortals. We would also be omnipotent.
What being could possess such God-like power? The answer: a being from a higher-dimensional world. Of course, these feats are beyond the capability of any three-dimensional person. For us, walls are solid and prison bars are unbreakable. Attempting to walk through walls will only give us a painful, bloody nose. But for a four-dimensional being, these feats would be child’s play.
To understand how these miraculous feats can be performed, consider again Gauss’s mythical two-dimensional beings, living on a two-dimensional table top. To jail a criminal, the Flatlanders simply draw a circle around him. No matter which way the criminal moves, he hits the impenetrable circle. However, it is a trivial task for us to spring the prisoner from jail. We just reach down, grab the Flatlander, peel him off the two-dimensional world, and redeposit him elsewhere on his world (
Figure 2.6
). This feat, which is quite ordinary in three dimensions, appears fantastic in two dimensions.
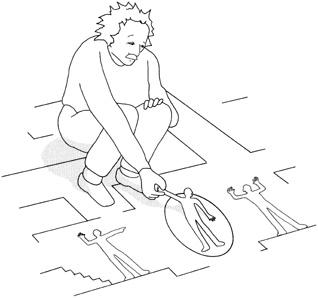
Figure 2.6. In Flatland, a “jail” is a circle drawn around a person. Escape from this circle is impossible in two dimensions. However, a three-dimensional person can yank a Flatlander out of jail into the third dimension. To a jailer, it appears as though the prisoner has mysteriously vanished into thin air
.
To his jailer, the prisoner has suddenly disappeared from an escape-proof prison, vanishing into thin air. Then just as suddenly, he reappears somewhere else. If you explain to the jailer that the prisoner was moved “up” and off Flatland, he would not understand what you were saying. The word
up
does not exist in the Flatlander’s vocabulary, nor can he visualize the concept.
The other feats can be similarly explained. For example, notice that the internal organs (like the stomach or heart) of a Flatlander are completely visible to us, in the same way that we can see the internal structure of cells on a microscope slide. It’s now trivial to reach inside a Flatlander and perform surgery without cutting the skin. We can also peel the Flatlander off his world, flip him around, and put him back down. Notice that his left and right organs are now reversed, so that his heart is on the right side (
Figure 2.7
).
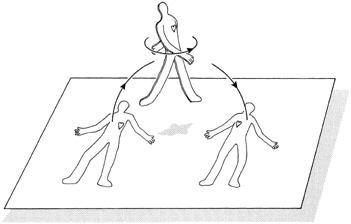
Figure 2.7. If we peel a Flatlander from his world and flip him over in three dimensions, his heart now appears on the right-hand side. All his internal organs have been reversed. This transformation is a medical impossibility to someone who lives strictly in Flatland
.
Viewing Flatland, notice also that we are omnipotent. Even if the Flatlander hides inside a house or under the ground, we can see him perfectly. He would regard our powers as magical; we, however, would know that not magic, but simply a more advantageous perspective, is at work. (Although such feats of “magic” are, in principle, possible within the realm of hyperspace physics, we should caution, once again, that the technology necessary to manipulate space-time far exceeds anything possible on the earth, at least for hundreds of years. The ability to manipulate space-time may be within the domain of only some extraterrestrial life in the universe far in advance of anything found on the earth, with the technology to master energy on a scale a quadrillion times larger than our most powerful machines.)
Although Riemann’s famous lecture was popularized by the work of Helmholtz and many others, the lay public could make little sense of this or the eating habits of two-dimensional creatures. For the average
person, the question was more direct: What kind of beings can walk through walls, see through steel, and perform miracles? What kind of beings are omnipotent and obey a set of laws different from ours?
