Grid of the Gods (44 page)

Note carefully the
implications
of this musical-topological metaphor, for clearly, it is not impaled on the horns of the either-or dialectic of having to choose between “pure monotheism” — a “feminine” principle in terms of the ancient worldview — nor a “pure polytheism”, or “masculine” principle in terms of the ancient worldview. The metaphor is an acid drip on that conventional opposition, for what one is looking at is an “androgynous both-and,” one encompassing both unity and diversity, and attempting to relate the two in a carefully conceived topological and musical metaphor.

The musical metaphor of the circles also lies behind the “churning of the Milky Sea”, for the diversity of the universe, as we saw at Angkor Wat, arises from the tension created by Vishnu’s original “tripartation” or differentiation. Rotation, understood in
musical terms, in the terms of
frequencies
, is the key.
²⁹
It goes without saying that
spin
and rotation moment are crucial concepts in distinguishing sub-atomic particles; thus as we shall see in chapter 13, there may be even deeper meanings to these ancient metaphors. There is even a dimension of Vedic teaching which relates all this cosmological topology and music to consciousness itself, for Soma, the magical food and drink of the gods that confers expanded consciousness, does so first of all by bringing insight into the musical experience as being comprised of the theory of numbers.
³⁰

From the musical point of view, however, the Vedic philosophy never completely reconciled the two cycles arising from unity, namely, the cycle of thirds, and the cycle of fifths. To put it differently, it never completely integrated the “female” octave with the “male” notes
within
that octave, and thus, any number of types of scales could be generated, all of which were, from the Vedic cosmological standpoint, equally valid.
³¹
The task of effecting that union and taking the first steps to our modern system of “equal tempering” or tuning was taken in Mesopotamia, and with its sexagesimal system of arithmetic.

D. The Sexagesimal System, Music, and Cosmology

It was in fact the famous Sumerologist Samuel Noah Kramer who located the fabled Sumerian “land of the gods,” Dilmun, with the “Harappan culture of pre-Vedic India.”
³²
By the time of the high Mesopotamian cultures, however, Vedic mathematical prowess had grown to enormous sophistication.

It is startling to learn…that the art of calculation in the third millenium (sic) Babylon — before the time of Abraham — was already comparable in many aspects with the mathematics “of the early Renaissance,” thirty-odd centuries later. Computation was made easy by the possession of tables (of which we have many copies) of “reciprocals, multiplications, squares and square roots, cubes, and cube roots, the sums of squares and cubes…
exponential functions, coefficients giving numbers for practical computation… and numerous metrological calculations giving areas of rectangles, circles,” etc. The Pythagoran theorem was known in Babylon “more than a thousand years before Pythagoras.” The foundations were laid for the discovery of the irrationality of √2 “exactly in the same arithmetical form in which it was obviously re-discovered so much later by the Greeks.” Traditional stories of discoveries made by Thales or Pythagoras must be discarded as “totally unhistorical”; much of what we have thought was Pythagorean must now be credited to Babylon.
³³

The implications, for McClain, are enormous, for this means that

The Hebrew Bible is thus the product of a Semitic culture which had mastered the fundamentals of music and mathematics a thousand years and more before its oldest pages were written. The stage was set for mathematical allegory on a grander scale than the relatively late Christian civilization has ever realized.
³⁴

Indeed, as will be seen, the Hebrew version of this mathematical and musical metaphor constitutes a step of trying to
edit and invert
the inherited Mesopotamian musical and mathematical metaphors of the “god of the mountain.”

In this musical mathematical allegory, McClain notes that its sexagesimal system of whole number integers was “probably the most convenient language for acoustical arithmetic the world ever knew” until the rise of logarithmic computation introduced in the nineteenth century of our era.
³⁵
Here we must also pause to note something that was observed in the previous book in this series,
Genes, Giants, Monsters, and Men,
namely, that the ancient systems of measures, and in particular, the Sumerian sexagesimal system, were also based
on astronomical and geodetic measures
,
³⁶
in other words, one is not only looking at a musical system of numbering, but on a
cosmological and geodetic one. Quite literally, the three cannot be disentangled; one is literally looking at the music of the planets, the music of the medium itself. The musical advantage is that it allows one to retain the uses of the “female” even numbers generating the octave matrix and the male numbers, based on powers and multiples of 3 and 5, generating the rest of the twelve tones, as in the ratio 30:60, a ratio that is based on multiples of 2, 5 and 6. Note also that the ratio can be reduced to 3:6, which can be reduced to the female number of 2; and that 60:5 is, of course, 12, giving the 12 tones of the chromatic scale, and, for the Mesopotamians, the 12 houses of the Zodiac. Succinctly stated, it is in the sexagesimal system that cosmology, music, number theory, and physics all meet in a harmonious whole.
³⁷

But what of the “gods” themselves, and our formula “Mountains ≈ Planets ≈ Gods ≈ Pyramids ≈ Music?” Why did the gods become associated with mountains and music?

It so happens that within Mesopotamia numerological mythology, that the three principle gods, Ea-Enki, Enlil, and Anu, are all numerically, and therefore, musically related, Ea-Enki having the value of 40, Enlil the value of 50, and Anu the value of 60, which, in the sexagesimal system, is also representative of the primordial unity, or 1. In musical terms, if one assigns a fundamental tone — say in this case, the note D — to An, then Enlil represents a third up or down from that (f or b), and Ea-Enki a fourth down or up (A or G), and from Enki, then, the entire circle of fourths and therefore all twelve tones, would be generated.
³⁸
Note that the ratio of these three gods is 40:50:60, or 4:5:6. From them, the whole modern twelve-note chromatic “tonal universe” is generated, as in our circle of fourths example above.
³⁹

If all this seems dense and obscure, it’s about to become even more so, for in the ultimate example of the “unified intention of symbol,” the numerical-musical allegory is reproduced in Berossus’ version of the Kings’ List of kings before the Flood:

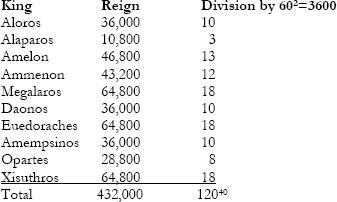
Note that the total, when divided by the quintessential Mesopotamian sexagesimal number of 3600, is 120, a harmonic of 12, our twelve chromatic tones once again.

In order to understand how all this relates to our musical tone circles, we have to look closer at Ea-Enki, whose numerological value is
⁴⁰
. To understand
how
this is so, it is important to remember that every whole number, when viewed
musically
, is viewed
in some ratio to the number sixty
, but the Mesopotamians do not actually
write
that second number. Thus, Enki’s number, 40, is really the ratio 40:60, or 2:3, an essential musical relationship in generating the twelve tones, for as such, he is the “first born son” of Anu, that is, “the first odd, hence male integer.”
⁴¹
As god of the “sweetwaters,” Enki is also “the Sumerian counterpart to the Greek Poseidon” and thus intricately related to the myth of Atlantis.
⁴²

E. Music and Higher-Dimensional Geometries:
The Musical Gods of the Musical Mountains

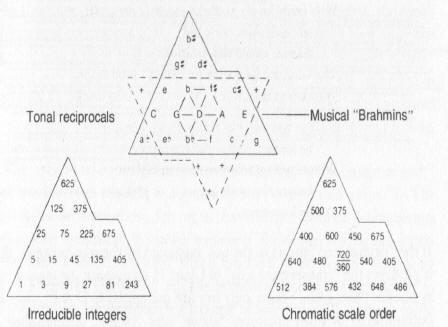
Enki, with 2:3 as his numbers, thus is a metaphor for the powers and multiples of 3 and 5, and here we come to the crux of the matter, for when these powers are graphed, a “numerical mountain” results, which we have followed by showing McClain’s graph of the “irreducible” integers and the tonal “zigurrats,” as McClain calls them, or mountains that result.

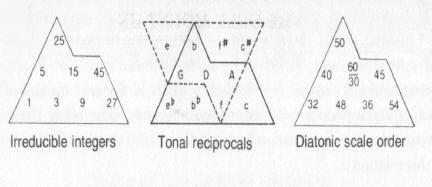
McClain’s “Tonal Zigurrats”
⁴³

Similarly, Enlil, whose number is 50, that is to say, 50:60 in the Mesopotamian scheme of ratios, and Marduk, laying at 25, both generated their own numerical tonal mountains.

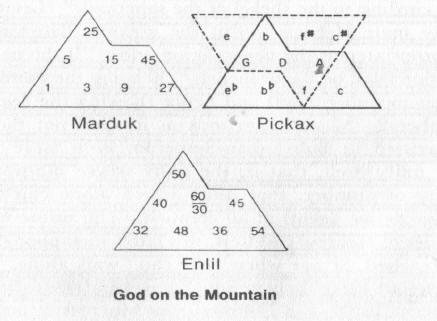
McClain’s Babylonian Gods of the Mountain
⁴⁴

Note the “Pickax” form of tones and their reciprocals (represented by the dotted “upside down ’mountain’”), for if one does a rotation of that mountain on its side so that the numbers on Marduk?s Mountain, which represent the tones generated in the pickax, can a common shared generating point in the number one, we get this:

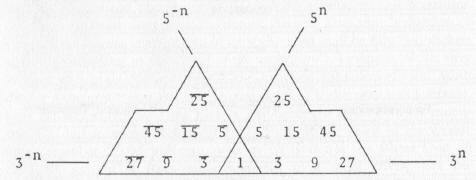
McClain’s Diagram of Twin-Peaked Mt. Mashu
⁴⁵

Note that on the horizontal line extending in each direction we have the initial unity, its first “tripartation” represented by 3 and 5 on the horizontal and diagonal, and on the horizontal, powers of three extending into infinity, and on the diagonal, powers of 5 extending into infinity, and between them, multiples of 3 and 5.

If we overlay the extended version of these tonal mountains over each other, we obtain an analogue of a familiar, and very Babylonian, figure, the “Star of David:”