Gödel, Escher, Bach: An Eternal Golden Braid (83 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

Achilles:
It is?
Tortoise: Yes, it is. Well, actually, it's my uncle's birthday, but that's almost the same.
How would you like to treat me to a delicious birthday dinner this evening?
Achilles: Now just a cotton-picking minute, Mr. T. Today is MY birthday. You should do the treating!
Tortoise: Ah, but you never did succeed in convincing me of the veracity of that remark.
You kept on beating around the bush with answers, Answer Schemas, and whatnot.
All I wanted to know was if it was your birthday or not, but you managed to befuddle me entirely. Oh, well, too bad. In any case, I'll be happy to let you treat me to a birthday dinner this evening.
Achilles: Very well. I know just the place. They have a variety of delicious soups. And I know exactly what kind we should have ...
Jumping out of the System
A More Powerful Formal System
ONE OF THE things which a thoughtful critic of Gödel’s proof might do would be to examine its generality. Such a critic might, for example, suspect that Gödel has just cleverly taken advantage of a hidden defect in one particular formal system, TNT. If this were the case, then perhaps a formal system superior to
TNT
could be developed which would not be subject to the Gödelian trick, and Gödel’s Theorem would lose much of its sting. In this Chapter we will carefully scrutinize the properties of
TNT
which made it vulnerable to the arguments of last Chapter.
A natural thought is this: If the basic trouble with
TNT
is that it contains a "hole"-
in other words, a sentence which is undecidable, namely
G
-then why not simply plug up the hole? Why not just tack
G
onto
TNT
as a sixth axiom? Of course, by comparison to the other axioms,
G
is a ridiculously huge giant, and the resulting system-
TNT+G
-would have a rather comical aspect due to the disproportionateness of its axioms. Be that as it may, adding
G
is a reasonable suggestion. Let us consider it done. Now, it is to be hoped, the new system,
TNT+G
, is a superior formal system-one which is not only supernatural-free, but also complete. It is certain that
TNT+G
is superior to
TNT
in at least one respect: the string
G
is no longer undecidable in this new system, since it is a theorem.
What was the vulnerability of
TNT
due to? The essence of its vulnerability was that it was capable of expressing statements about itself-in particular, the statement
"I Cannot Be Proven in Formal System
TNT
"
or, expanded a bit,
"There does not exist a natural number which forms a
TNT
-proof-pair with the Gödel number of this string."
Is there any reason to expect or hope that
TNT+G
would be invulnerable to Gödel’s proof? Not really. Our new system is just as expressive as
TNT
. Since Gödel’s proof relies primarily on the expressive power of a formal system, we should not be surprised to see our new system succumb,
too. The trick will be to find a string which expresses the statement
"I Cannot Be Proven in Formal System
TNT+G
."
Actually, it is not much of a trick, once you have seen it done for
TNT
. All the same principles are employed: only, the context shifts slightly. (Figuratively speaking, we take a tune we know and simply sing it again, only in a higher key.) As before, the string which we are looking for-let us call it "
G
"'-is constructed by the intermediary of an
"uncle", But instead of being based on the formula which represents
TNT
-proof-pairs, it is based on the similar but slightly more complicated notion of
TNT+G
-proofpairs. This notion of
TNT+G
-proof-pairs is only a slight extension of the original notion of'
TNT
-
proof-pairs.
A similar extension could be envisaged for the
MIU
-system. We have seen the unadulterated form of
MIU
-proof-pairs. Were we now to add MU as a second axiom, we would be dealing with a new system-the
MIU+MU
system. A derivation in this extended system is presented:
MU
axiom
MUU
rule 2
There is a
MIU+MU
-proof-pair which corresponds-namely, m = 30300, n = 300. Of course, this pair of numbers does not form a
MIU
-proof-pair-only a
MIU+MU
-proofpair. The addition of an extra axiom does not substantially complicate the arithmetical properties of proof-pairs. The significant fact about them-that being a proof-pair is primitive recursive-is preserved.
The Gödel Method Reapplied
Vow, returning to
TNT+G
, we will find a similar situation
. TNT+G
proof-pairs, like their predecessors, are primitive recursive, so they are represented inside
TNT+G
by a formula which we abbreviate in an obvious manner.
(TNT+G)-PROOF-PAIR{a,a' }
Vow we just do everything all over again. We make the counterpart of
G
by beginning with an "uncle", just as before:
3a:3a':<(TNT+G)-PROOF-PAIR{a,a'}ARITHMOQUINE{a",a'}>
.et us say its Gödel-number is u'. Now we arithmoquine this very uncle. That will give us
G
':
3a:3a': < (TNT+G)-PROOF-PAIR{a,a' }
ARITHMOQUINE{SSS….SSSo/a´´,a´}>
UŚś
Its interpretation is
"There is no number
a
that forms a
TNT +G
-proof-pair with the arithmoquinification of
u
'."
More concisely,
"I Cannot Be Proven in Formal System
TNT+G
."
Multifurcation
Well (yawn), the details are quite boring from here on out. G' is precisely to
TNT+G
as
G
was to
TNT
Itself. One finds that either
G
' or -
G
' can be added to
TNT+G
, to yield a further splitting of number theory. And, lest you think this only happens to the "good guys", this very same dastardly trick can be played upon
TNT+--G
-that is, upon the nonstandard extension of
TNT
gotten by adding
G
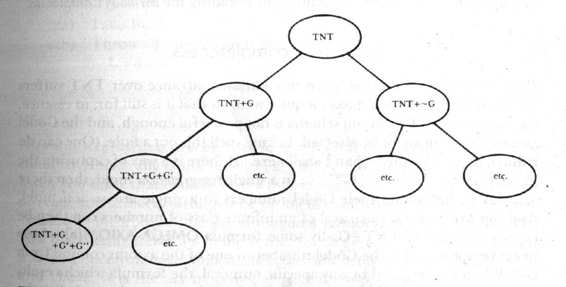
's negation. So now we see (Fig. 75) that there are all sorts of bifurcations in number theory:
FIGURE 75. "Multifurcation" of
TNT
. Each extension of
TNT
has its very own Gödel
sentence; that sentence, or its negation, can be added on, so that from each extension
there sprouts a pair of further extensions, a process which goes on ad infinitum.
Of course, this is just the beginning. Let us imagine moving down the leftmost branch of this downwards-pointing tree, where we always toss in the Gödel sentences (rather than their negations). This is the best we can do by way of eliminating supernaturals. After adding
G
, we add
G
'. Then we add
G
", and
G
"', and so on. Each time we make a new extension of
TNT
, its vulnerability to the Tortoise's method-pardon me, I mean Gödel’s method.. allows a new string to be devised, having the interpretation.
“I cannot be proven in formal system X”
Naturally, after a while, the whole process begins to seem utterly predictable and routine.
Why, all the "holes" are made by one single technique! This means that, viewed as typographical objects, they are all cast from one single mold, which in turn means that one single axiom schema suffices to represent all of them! So if this is so, why not plug up all :he holes at once and be done with this nasty business of incompleteness 3nce and for all? This would be accomplished by adding an axiom schema to
TNT
, instead of just one axiom at a time. Specifically, this axiom schema would be the mold in which all of
G, G', G", G
"', etc., are cast. By adding :his axiom schema (let's call it "
G~
"), we would be outsmarting the "Gödelization" method. Indeed, it seems quite clear that adding
G
. to
TNT
would :)e the last step necessary for the complete axiomatization of all of numbertheoretical truth.
It was at about this point in the Contracrostipunctus that the Tortoise related the Crab's invention of "Record Player Omega". However, readers were left dangling as to the fate of that device, since before completing his tale, the tuckered-out Tortoise decided that he had best go home to sleep; but not before tossing off a sly reference to Gödel’s Incompleteness Theorem). Now, at last, we can get around to clearing up that dangling detail ... Perhaps you already have an inkling, after reading the Birthday Cantatatata.
Essential Incompleteness
As you probably suspected, even this fantastic advance over
TNT
suffers the same fate.
And what makes it quite weird is that it is still for, in essence, the same reason. The axiom schema is not powerful enough, and the Gödel construction can again be effected.
Let me spell this out a little. (One can do it much more rigorously than I shall here.) If there is a way of capturing the various strings
G, G', G", G
"' . . in a single typographical mold, then there is a way of describing their Gödel numbers in a single arithmetical mold.
And this arithmetical portrayal of an infinite class of numbers can then be represented inside
TNT+G
. by some formula
OMEGA-AXIOM
{a} whose interpretation is: "a is the Godel number of one of the axioms coming from
G
.". When a is replaced by any specific numeral, the formula which results will be a theorem of
TNT+G
. if and only if the numeral stands for the Gödel number of an axiom coming from the schema.
With the aid of this new formula, it becomes possible to represent even such a complicated notion as
TNT+G
.-proof-pairs inside
TNT+Gω
:
(TNT+G.)- PROOF- PAIR{a, a' )
sing this formula, we can construct a new uncle, which we proceed to Arithmoquine in the by now thoroughly familiar way, making yet another undecidable string, which will be called "
TNT+Gω+i
". At this point, you might well wonder, "Why isn't
Gω+i
among the axioms created by the axiom schema
Gω
?”
The answer is that
G
was not clever enough to foresee its own embeddability inside number theory.
In the Contracrostipunctus, one of the essential steps in the Tortoise's making an
"unplayable record" was to get a hold of a manufacturer's blueprint of the record player which he was out to destroy. This was necessary so that he could figure out to what kinds of vibrations it was vulnerable, and then incorporate into his record such grooves as would code for sounds which would induce those vibrations. It is a close analogue to the Gödel trick, in which the system's own properties are reflected inside the notion of proofpairs, and then used against it. Any system, no matter how complex or tricky it is, can be Gödel-numbered, and then the notion of its proof-pairs can be defined-and this is the petard by which it is hoist. Once a system is well-defined, or "boxed", it becomes vulnerable.
This principle is excellently illustrated by the Cantor diagonal trick, which finds an omitted real number for each well-defined list of reals between 0 and 1. It is the act of giving an explicit list-a "box" of reals which causes the downfall. Let us see how the Cantor trick can be repeated over and over again. Consider what happens if, starting with some list L, you do the following:
(la) Take list L, and construct its diagonal number d.
(lb) Throw d somewhere into list L, making a new list L+d.
(2a) Take list L +d, and construct its diagonal number d'.
(2b) Throw d' somewhere into list L+d, making a new list L+d+d'.
Now this step-by-step process may seem a doltish way to patch up
L
, for we could have made the entire list
d, d', d", d
"', ... at once, given
L
originally. But if you think that making such a list will enable you to complete your list of reals, you are very wrong. The problem comes at the moment you ask, "Where to incorporate the list of diagonal numbers inside
L
?" No matter how diabolically clever a scheme you devise for ensconcing the d-numbers inside L, once you have done it, then the new list is still vulnerable. As was said above, it is the act of giving an explicit list-a "box" of reals-that causes the downfall.
Now in the case of formal systems, it is the act of giving an explicit recipe for what supposedly characterizes number-theoretical truth that causes the incompleteness.
This is the crux of the problem with
TNT+Gω
,. Once you insert all the
G
's in a well-defined way into TNT, there is seen to be some other G-some unforeseen
G
-which you didn't capture in your axiom schema. And in the case of the
TC
-battle inside the
ContracrostiPunctus
, the instant a record player's "architecture" is determined, the record player becomes capable of being shaken to pieces.
