Full House (23 page)

I therefore have little confidence that we can specify a clear bias one way or the other on general principles. But we do have a wealth of empirical data available for study. After all, the founding species of most multicellular lineages does not begin at a wall—and subsequent evolution remains free to produce either more or less complex species. If we can agree on a measure of complexity, and document enough lineages, we may be able to extract a general conclusion. This subject has just begun to interest paleontologists in the past few years. We have not yet compiled nearly enough cases for any confident general solution. But the initial studies offer great promise, for we have at least made this vital subject tractable and testable. And the first few cases all point in the same radical direction— no bias toward increasing complexity has yet been measured.

This line of research has been pioneered by Dan McShea of the University of Michigan, now at Santa Fe’s Institute for the Study of Complexity. Much of the technical literature must focus on providing an unambiguous and quantifiable definition for a very fuzzy vernacular term with a wide variety of meanings, some contradictory—namely, complexity itself. What do we mean when we say that a thing is more complex than something else? Several criteria fit our vernacular sense, depending upon the context. Complexity has morphological, developmental, and func
_-
tional aspects. A junk heap (to use an example favored by McShea and Thomas) may be morphologically very complex (in consisting of so many highly varied and independent parts) but functionally quite simple (just glop for a landfill). On the other hand, what is functionally simple for us might be quite complex to other users—in this case, to the seagull who must distinguish all the little bits while searching for morsels of food.

I do not wish to address this technical subject at length in a book for general readers (but see McShea, 1992, 1993, 1994, and Thomas, 1993, for interesting discussion), though the importance and nature of the problem must be recorded. I do not think that any general solution can be found— because "complexity" is a vernacular term with several legitimately different meanings, and we may well be interested in all of them. For science as "the art of the soluble" (to use P. B. Medawar’s felicitous phrase)—an enterprise dedicated to posing answerable questions—we must only resolve that we will choose a rigorously quantifiable definition of complexity and be very clear about which aspects of vernacular meaning will be thus addressed, and which omitted. (Someone else, or you yourself in a subsequent study, may then measure other aspects of complexity.) The literature has been admirable on this account, and therefore happily free of the muddiness that accompanies so much science.

McShea has favored a morphological definition—not because he views this meaning as closer to some vernacular norm, but because it permits well-defined measurement and rigorous testing. He writes (1996): "The point is to rescue the study of biological complexity from a swamp of impressionistic evaluations, biased samples, and theoretical speculations, and to try to place it on more solid empirical ground." McShea employs the following conceptualization to construct his quantifications:

The complexity of a system is generally acknowledged to be some function of the number of different parts it has, and of the irregularity of their arrangement. Thus, heterogenous, messy, or irregularly configured systems are complex, such as organisms, automobiles, compost heaps, and junk yards. Order is the opposite of complexity. Ordered systems are homogeneous, redundant, or regular, like picket fences and brick walls (1993, page 731).

In his major study of the vertebrate spinal column, for example, McShea (1993) operationalizes this definition by measuring complexity as the degree to which individual vertebrae differ among themselves. (In the less complex backbone of a fish, forty or more vertebrae may be effectively alike as simple discs of similar size; the more complex mammalian spine has fewer vertebrae differentiated into the varied forms and sizes of neck bones, back vertebrae, and sacral discs that support the pelvis.) In practice (see Figure 32), McShea measures six variables (five linear dimensions and an angle) on each vertebra and then calculates the difference among vertebrae. He uses three assessments of complexity as variation among vertebrae: (1) the maximal difference between any two vertebrae of the same spinal column; (2) the average difference between each vertebra and the mean for all vertebrae; and (3) the average difference between each pair of adjacent vertebrae.

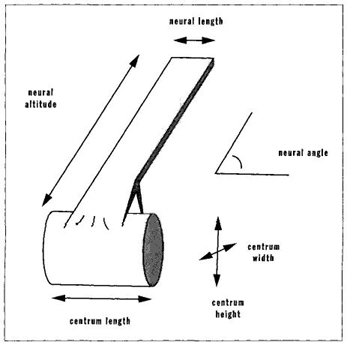
FIGURE 32 Measurements used by McShea to assess the history of complexity in vertebrae.

McShea’s framework for testing harmonizes perfectly with the perspective of this book. He holds that trends come in two basic modes with strikingly different fundamental causes. He names these categories driven and passive, and argues that they represent natural "kinds," not just conceptual conveniences for human understanding. He writes (1994, page 1762): "These results do raise the possibility that the passive and driven mechanisms may be natural categories and that they may correspond to distinct and well-defined causes of large-scale trends."

Driven trends correspond to the traditional view of an overall movement achieved because each element evolves with a bias for change in this direction. A driven trend to complexity would arise because evolution generally favors more complex creatures—and each species of a lineage therefore tends to change in this manner. (In other words, natural selection acts as a driver, conveying each vehicle in a favored direction.) Passive trends (see Figure 33) conform to the unfamiliar model, championed for complexity in this book, of overall results arising as incidental consequences, with no favored direction for individual species. (McShea calls such a trend passive because no driver conducts any species along a preferred pathway. The general trend will arise even when the evolution of each individual species confirms to a "drunkard’s walk" of random motion.) For passive trends in complexity, McShea proposes the same set of constraints that I have advocated throughout this book: ancestral beginnings at a left wall of minimal complexity, with only one direction open to novelty in subsequent evolution.

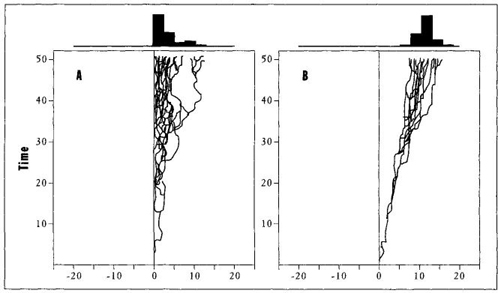
FIGURE 33 Passive and driven trends in McShea’s terminology. A passive trend (A) begins near a left wall, retains a constant mode at this beginning position, and expands in the only open direction toward the right. In a driven trend (B), both minimum and maximum values increase through time.

McShea proposes three tests for distinguishing driven from passive trends:

1. THE TEST OF THE MINIMUM. In passive systems, minimum values of complexity should be preserved by some species throughout the expanding history of a lineage because no general evolutionary preference for complexity exists, and some species should therefore do best by remaining simple. In driven systems, both minimum and maximum complexity should increase through time because higher complexity confers such general advantages that evolution of all species should be biased in this direction. (The preservation and continuing enhancement of life’s bacterial mode strongly points to the passive mode for life as a whole.)

This test, although indicative, does not fully distinguish passive from driven trends because even a driven trend might permit a few species to retain minimal values. (In a driven trend, the minimum might not disappear, but these lowest values should at least become less frequent over time.)

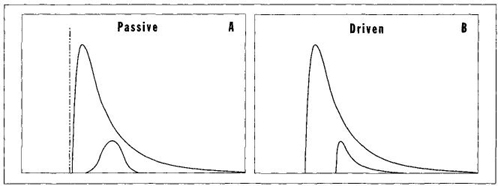
FIGURE 34 A test to distinguish passive from driven trends. The entire distribution for the passive trend should be right skewed, but component lineages that begin far away from the left wall should have normal distributions.

2. THE TEST OF ANCESTOR-DESCENDANT PAIRINGS. This powerful and obvious test identifies an ancestral species for an expanding lineage and then simply tabulates all descendants to judge whether most become more complex, simpler, or stay the same. In principle this is the most decisive test of all. But in practice we cannot always use it because the fossil record is so imperfect. We often do not know the ancestral species, or we do not have enough descendants to make a proper randomized test of subsequent directions.

3. THE TEST OF SKEWING. For life-as-a-whole, both the passive and driven mechanism can produce the same overall result of a right-skewed distribution with an expanding tail at maximal complexity. McShea argues that we might distinguish passive from driven modes by studying the skewness of component lineages that begin far from the wall and can therefore vary in either direction (see Figure 34). In driven systems, the component lineages should also tend to be right skewed because all species experience the bias of progress as a favored direction and should therefore contain more species moving along this preferred pathway, thereby stretching the entire distribution toward the right. But in passive systems, component lineages should develop no skew because increases and decreases in individual species should be equally common—that is, as many species should move leftward to less complexity as rightward to more elaboration.

In his major study, McShea (1993, 1994) has applied these tests to evolution of the vertebral column. A general trend obviously exists for vertebrates as a whole because the first vertebrates were fishes with a backbone built of essentially identical elements, while later mammals evolved considerable variation among vertebrae along the spinal column. But is this trend passive or driven? (Tradition says driven, but one fact certainly leaves maximal "room" for passivity. Much like the initial living thing at the left wall of minimal complexity, or the founding foraminiferal species at the absolute left wall of minimal sieve size [see pages 157—158], vertebrates begin at a theoretically minimal value of complexity by McShea’s measurements. Since the founding fishes tend to have vertebral columns made of identical elements, their measured complexity will be close to flat zero [McShea measures complexity as differences among vertebrae]. There really is no place to go from this initial point but up!)

McShea’s study of sublineages within mammals provides strong quantitative evidence for increasing general complexity in the passive mode— thus supporting the claim of this book that no explicit preference or bias for complexity acts as a driving force in the evolution of life. McShea surveyed five sublineages where he could identify or infer an ancestor, thus permitting him to use the most powerful second test: ruminant mammals (the large group of cud-chewing cattle, deer, etc.); squirrels of the large family Sciuridae; the entire order of pangolins (a group of armored anteaters, now represented by the genus Manis of Africa and Asia); whales; and camels.

All the tests provide evidence for a passive trend and no drive to complexity. McShea found twenty-four cases of significant increases or decreases in comparing the range of modern descendants with an ancestor (out of a total potential sample of ninety comparisons, or five groups of mammals, each with six variables measured in each of three ways; for the other comparisons, average descendants did not differ significantly from ancestors). Interestingly, thirteen of these significant changes led to decreases in complexity, while only nine showed increase. (The difference between thirteen and nine is not statistically significant, but I am still wryly amused, given all traditional expectation in the other direction, that more comparisons show decreasing rather than increasing complexity.)