Full House (18 page)

My colleague Anthony J. Arnold, along with his associates D. C. Kelly and W. C. Parker of Florida State University, have now supplied the missing information. Using a remarkable set of data on known pairings of ancestors with descendants in 342 Cenozoic species of planktonic forams, they plotted the bell curve for differences in size between descendants and their immediate ancestors. A zero value in Figure 26 indicates that the descendant arose at the same size as the ancestor, a negative value marks a smaller descendant, and a positive value a larger descendant. The symmetrical, unskewed bell curve of Figure 26 proves that no tendency exists for either increase or decrease of size in the origin of new species in planktonic forams. A descendant is just as likely to arise at either a smaller or a larger size than its ancestor. Arnold, Kelly, and Parker (1995, page 206) state their clear conclusion: "There is no apparent ... tendency to favor size increase; there is no strong indication of size-dependent longevity, and there is no indication of size dependence in speciation or extinction rates."
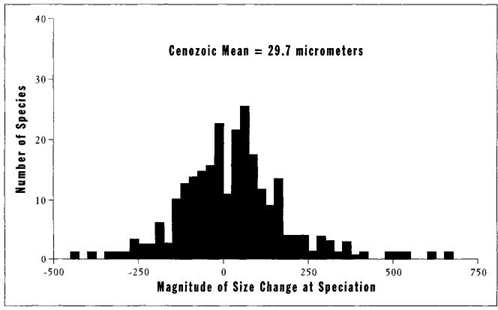
FIGURE 26 Evidence that no preference for increasing size exists in speciation events during the evolution of forams. Values greater than zero on the horizontal axis indicate size increase; values less than zero indicate size decrease in a speciation event. The normal distribution shows no preference for either increase or decrease during evolution.
Yet the size of the largest species, and the mean value, do increase within each act. How shall we interpret this phenomenon if we must deny—as a proper examination of variation in the full system says we must—any overall tendency or general advantage to increasing size? Ironically, we seem to need an explanation precisely backwards from the usual claim (the "manifest" and "obvious" superiority of large size, now discredited). The entire phenomenon arises from three factors: (1) the existence of a left wall, a true lower limit to size in this case, set by the artifact of minimum mesh in conventional laboratory sieves; (2) the survival of small-bodied species alone (near the minimal size) after each episode of mass extinction, and the consequent beginning of each act only with species at the lower end of the size range; and (3) successful radiation and increase in number of species within each act, so that total diversity grows through time in each case.
Given these three conditions, we note an increase in size of the largest species only because founding species start at the left wall, and the range of size can therefore expand in only one direction. Size of the most common species (the modal decade) never changes, and descendants show no bias for arising at larger sizes than ancestors. But, during each act, the range of size expands in the only open direction by increase in the total number of species, a few of which (and only a few) become larger (while none can penetrate the left wall and get smaller). We can say only this for Cope’s Rule: in cases with boundary conditions like the three listed above, extreme achievements in body size will move away from initial values near walls. Size increase, in other words, is really random evolution away from small size, not directed evolution toward large size.
Please understand that I am not depriving this story of great interest and importance, and I am not denying that the size of the largest species increases with time. I am saying that proper consideration of expanding variation within the full system, rather than myopic focus on mean or extreme values ("things moving somewhere"), forces us to reinterpret the case in a manner opposite to the usual reading. Under the conventional view we asked why selection favored large size. In the new interpretation we need to know (and we do not) why small-bodied species differentially survived in episodes of mass extinction to begin each new episode of evolution with just a few species at nearly minimal size. Everything else simply follows from this limited beginning and the group’s expanding success.
The necessity (and fascination) of such an inverted interpretation in this case suggests that we might profitably reassess the entire phenomenon of Cope’s Rule, one of the oldest "received truths" in paleontology and evolutionary theory. I do not doubt that some instances may be best explained under the old rubric of "things moving somewhere"—that is, as general increases in size for all or most lineages in a group as a result of selective advantage for larger bodies (and not as expansion of variation in a full system, misread as a trend in extreme values).
But a survey of all cases will surely alter our former certainty and will teach us to prefer full houses over abstracted averages or extremes if we wish to unravel both the phenomenology and the causality of evolutionary change in the fossil record. First of all, some venerable cases of Cope’s Rule are pure artifacts of a myopic focus upon extreme values. For example, my colleague David Jablonski of the University of Chicago studied patterns of change in size for all genera of clams with fossil records spanning more than 4 million years in late Cretaceous sediments of the Gulf and Atlantic Coastal Plain of the United States. He found that thirty-three of fifty-eight genera followed what he called the "broad" (I would say inappropriate) sense of Cope’s Rule, because the largest late representative exceeded the largest early representative in size. But he then found that, in twenty-two of these thirty-three genera, the size of the smallest species also decreased or remained stable in time. Thus, in at least two-thirds of the genera studied, "general" size increase records only our tendency to study the upper bound rather than the entire range. Jablonski concluded (1987, page 714) that "Cope’s Rule is driven by an increase in variance rather than a simple directional trend in body sizes."
In other, more legitimate cases, increases in means or extremes occur, as in our story of planktonic forams, because lineages started near the left wall of a potential range in size and then filled available space as the number of species increased—in other words, a drift of means or extremes away from small size, rather than directed evolution of lineages toward large size (and remember that such a drift can occur within a regime of random change in size for each individual lineage—the "drunkard’s walk" model).
In 1973, my colleague Steven Stanley of Johns Hopkins University published a marvelous, and now celebrated, paper to advance this important argument. He showed (see Figure 27, taken from his work) that groups beginning at small size, and constrained by a left wall near this starting point, will increase in mean or extreme size under a regime of random evolution within each species. He also advocated that we test his idea by looking for right-skewed distributions of size within entire systems, rather than by tracking mean or extreme values that falsely abstract such systems as single numbers. In a 1988 paper I suggested that we speak of "Stanley’s Rule" when such an increase of means or extremes can best be explained by undirected evolution away from a starting point near a left wall. I would venture to guess (in fact I would wager substantial money on the proposition) that a large majority of lineages showing increase of body size for mean or extreme values (Cope’s Rule in the broad sense) will properly be explained by Stanley’s Rule of random evolution away from small size rather than by the conventional account of directed evolution toward selectively advantageous large size.
In this context, and to conclude the chapter, I was delighted to discover (when studying Cope’s original formulation in order to write this part of my book) that Cope himself had grasped this better explanation "through a glass darkly." Cope did write a good deal about the phenomenon that would later be called "Cope’s Rule" or even "Cope’s Law." But he devoted much more attention to another putative law that he evidently regarded as much more important—his self-styled "law of the unspecialized" (Cope, 1896, pages 172-74).
This law states that founding members of highly successful lineages tend to be "unspecialized" in the sense that they can tolerate a wide range of habitats and climates, and that they do not possess complex and highly specific adaptations to narrow behaviors or modes of life (the peacock’s tail or the koala’s need to eat just one kind of eucalyptus leaf). With the proviso that such evolutionary laws have only majoritarian status (not exclusivity) in our complex and partly random world, Cope’s law of the unspecialized has held up well, and would be endorsed by evolutionary biologists today.
Cope himself recognized—and not just as a passing observation, for he repeated the point several times—that such unspecialized lineages also tend to be small in body size (and even that small size favors unspecialized status). But he never made the full connection that becomes so obvious in the light of this book’s central theme: maybe Cope’s now more famous law of increasing body size only arises as a noncausal side consequence of Cope’s other law of the unspecialized. Major lineages tend to be founded by species of unspecialized anatomy and behavior. Unspecialized species also tend to be small in body size. Cope’s Rule of increasing size is therefore an artifact of these small beginnings near a left wall for the founders of major lineages. Cope never made all the connections, but we should record and honor his words:
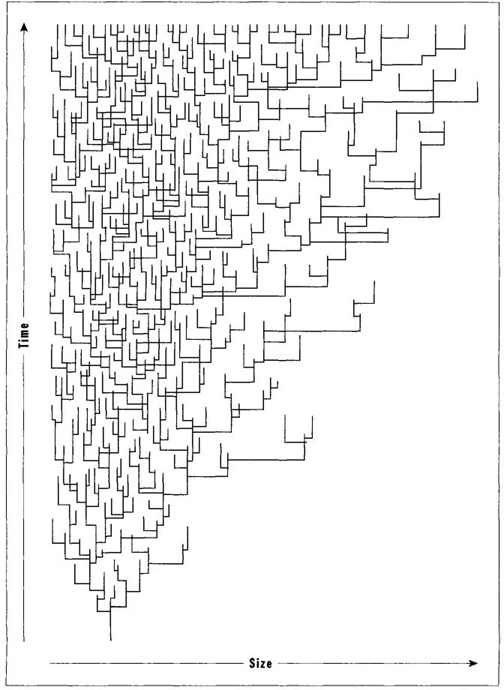
FIGURE 27 The increase in size of mean and extreme values within a branching evolutionary series arises in this case only as a function of origin near a lower limit, or left wall, in size.
The "Doctrine of the Unspecialized" ... describes the fact that the highly developed, or specialized types of one geological period have not been the parents of the types of succeeding periods, but that the descent has been derived from the less specialized of preceding ages.... The validity of this law is due to the fact that the specialized types of all periods have been generally incapable of adaptation to the changed conditions which characterized the advent of new periods.... Such changes have been often especially severe in their effects on species of large size, which required food in great quantities.... Animals of omnivorous food-habits would survive where those which required special foods would die. Species of small size would survive a scarcity of food, while large ones would perish. It is true ... that the lines of descent of Mammalia have originated or been continued through forms of small size. The same is true of all other Vertebrata.
14
The Power of the Modal Bacter, or Why the Tail Can’t Wag the Dog
An Epitome of the Argument
I believe that the most knowledgeable students of life’s history have always sensed the failure of the fossil record to supply the most desired ingredient of Western comfort: a clear signal of progress measured as some form of steadily increasing complexity for life as a whole through time. The basic evidence cannot support such a view, for simple forms still predominate in most environments, as they always have. Faced with this undeniable fact, supporters of progress (that is, nearly all of us throughout the history of evolutionary thought) have shifted criteria and ended up grasping at straws. (The altered criterion may not have struck the graspers as such a thin reed, for one must first internalize the argument of this book—trends as changes in variation rather than things moving somewhere—to recognize the weakness.) In short, graspers for progress have looked exclusively at the history of the most complex organism through time—a myopic focus on extreme values only—and have used the increasing complexity of the most complex as a false surrogate for progress of the whole (again, see this book’s opening example and Figure 1 for a striking case). But this argument is illogical and has always disturbed the most critical consumers.
Thus, James Dwight Dana, America’s greatest naturalist in Darwin’s era (at least after Agassiz’s death), and a soul mate to Darwin in their remarkably parallel careers (both went on long sea voyages in their youth, and both became fascinated with coral reefs and the taxonomy of crustaceans), used this criterion when he finally converted to evolution in the mid-1870s. Dana’s primary commitment to progress as the definition of life’s organization held firm throughout his career, and in his personal transition from creationism to evolution. But Dana could validate progress only by looking at the history of extremes—"the grand fact that the system of life began in the simple sea-plant and the lower forms of animals, and ended in man" (Dana, 1876, page 593). Julian Huxley, grandson of Thomas Henry, sensed the same unease, but could think of no other criterion in 1959 (as quoted at the beginning of chapter 12). When Darwin’s grandson challenged him to defend progress in the light of so many well-adapted but anatomically simplified parasites, Julian Huxley replied, "I mean a higher degree of organization in general, as shown by the upper level attained." But the "upper level attained" (the extreme organism at the right tail) is not a measure of "organization in general"—and Huxley’s defense is illogical.
In debunking this conventional argument for progress in the history of life, I reach the crux of this book (although I will not disparage anyone who regards baseball as equal in importance to life’s history, and therefore views the correct interpretation of 0.400 hitting as more vital to American life than understanding the central themes of 3.5 billion years in biological time)! Yet I can summarize my argument against progress in the history of life in just seven statements condensed into a few pages. I do not mean to be capricious or disrespectful in this brevity. If have done my job in the rest of this book, I have already set the background and argument with sufficient thoroughness—so this focal application at grandest scale should follow quickly with just a few reminders and way stations for the new context.
I do not challenge the statement that the most complex creature has tended to increase in elaboration through time, but I fervently deny that this limited little fact can provide an argument for general progress as a defining thrust of life’s history. Such a grandiose claim represents a ludicrous case of the tail wagging the dog, or the invalid elevation of a small and epiphenomenal consequence into a major and controlling cause.
I shall present, in seven arguments, my best sense of a proper case based on the history of expanding variation away from a beginning left wall. I shall then provide extended commentary for three of the statements that are particularly vital, and most generally misunderstood or unappreciated. Please note that the entire sequence of statements for life as a whole follows exactly the same logic, and postulates the same causes, as my previous story (at smallest scale) about the evolution of planktonic forams.
1. Life’s necessary beginning at the left wall. The earth is about 4.5 billion years old. Life, as recorded in the fossil record, originated at least 3.5 billion years ago, and probably not much earlier because the earth passed through a molten period that ended about 3.8 billion years ago (the age of the oldest rocks). Life presumably began in primeval oceans as a result of sequential chemical reactions based on original constituents of atmospheres and oceans, and regulated by principles of physics for self-organizing systems. (The "primeval soup" has long been a catchword for oceans teeming with appropriate organic compounds prior to the origin of life.) In any case, we may specify as a "left wall" the minimal complexity of life under these conditions of spontaneous origin. (As a paleontologist, I like to think of this wall as the lower limit of "conceivable, preservable complexity" in the fossil record.) For reasons of physics and chemistry, life had to begin right next to the left wall of minimal complexity—as a microscopic blob. You cannot begin by precipitating a lion out of the primeval soup.
2. Stability throughout time of the initial bacterial mode. If we are particularly parochial in our concern for multicellular creatures, we place the major division in life between plants and animals (as the Book of Genesis does in both creation myths of chapters 1 and 2). If we are more ecumenical, we generally place the division between unicellular and multicellular forms. But most professional biologists would argue that the break of maximal profundity occurs within the unicells, separating the prokaryotes (or cells without organelles—no nuclei, no chromosomes, no mitochondria, no chloroplasts) from the eukaryotes (organisms like amoebae and paramecia, with all the complex parts contained in the cells of multicellular organisms). Prokaryotes include the amazingly diverse groups collectively known as "bacteria," and also the so-called "blue-green algae," which are little more than photosynthesizing bacteria, and are now generally known as Cyanobacteria.
All the earliest forms of life in the fossil record are prokaryotes—or, loosely, "bacteria." In fact, more than half the history of life is a tale of bacteria only. In terms of preservable anatomy in the fossil record, bacteria lie right next to the left wall of minimal conceivable complexity. Life therefore began with a bacterial mode (see Figure 28). Life still maintains a bacterial mode in the same position. So it was in the beginning, is now, and ever shall be—at least until the sun explodes and dooms the planet. How, then, using the proper criterion of variation in life’s full house, can we possibly argue that progress provides a central defining thrust to evolution if complexity’s mode has never changed? (Life’s mean complexity may have increased, but see chapter 4 for a discussion of why means are inappropriate, and modes proper, as measures of central tendency in strongly skewed distributions.) The modal bacter of this chapter’s title has been life’s constant paradigm of success.

FIGURE 28 Life begins necessarily near the left wall of minimal complexity, and the bacterial mode soon develops.
3. Life’s successful expansion must form an increasingly right-skewed distribution. Life had to begin next to the left wall of minimal complexity (see statement 1). As life diversified, only one direction stood open for expansion. Nothing much could move left and fit between the initial bacterial mode and the left wall. The bacterial mode itself has maintained its initial position and grown continually in height (see Figure 29). Since space remains available away from the left wall and toward the direction of greater complexity, new species occasionally wander into this previously unoccupied domain, giving the bell curve of complexity for all species a right skew, with capacity for increased skewing through time.
4. The myopia of characterizing a full distribution by an extreme item at one tail. Considering life’s full house of Figure 29, the only conceivable argument for general progress must postulate that an expanding right tail demonstrates a predictable upward thrust of the whole. But such a claim only embodies the silly spectacle of a small tail wagging a large dog. (We have generally failed to grasp the evident absurdity because we have not visualized the dog properly; rather, in a move that recalls the Cheshire Cat of Wonderland, identified only by its smile, we have characterized the entire dog by its tail alone.)
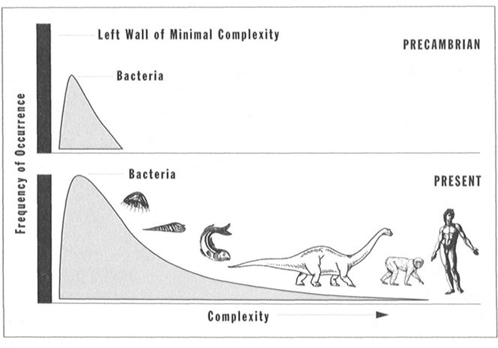
FIGURE 29 The frequency distribution for life’s complexity becomes increasingly right skewed through time, but the bacterial mode never alters.
A claim for general progress based on the right tail alone is absurd for two primary reasons: First, the tail is small and occupied by only a tiny percentage of species (more than 80 percent of multicellular animal species are arthropods, and we generally regard almost all members of this phylum as primitive and nonprogressive). Second, the occupants of the extreme right edge through time do not form an evolutionary sequence, but rather a motley series of disparate forms that have tumbled into this position, one after the other. Such a sequence through time might read: bacterium, eukaryotic cell, marine alga, jellyfish, trilobite, nautiloid, placoderm fish, dinosaur, saber-toothed cat, and Homo sapiens. Beyond the first two transitions, not a single form in this sequence can possibly be a direct ancestor of the next in line.
5. Causality resides at the wall and in the spread of variation; the right tail is a consequence, not a cause. The development of life’s bell curve for complexity through time (Figures 28 and 29) does not represent a fully random phenomenon (though random elements play an important role). Two important causal influences shape the curve and its changes—but neither influence includes any statement about conventional progress. The two major causes are, first, necessary origin at the left wall of minimal complexity; and, second, increase of numbers and kinds, with predictable development of a right-skewed distribution. Given this point of origin at a wall and subsequent increase in variation, the right tail almost had to develop and extend. But this expansion of the right tail—the only (and myopic) source for any potential claim about progress—is an epiphenomenon and a side consequence of the two causes listed above, not a fundamental thrust produced by the superiority of complex forms under natural selection. In fact, as the paradigm of the drunkard’s walk illustrates, such an extension of the right tail will occur in a regime of entirely random motion for each item, so long as the system begins at a wall. Thus, as the drunkard’s walk shows in theory, and the evolution of planktonic forams confirms in fact, the expanding right tail of life’s complexity may arise from random motion among all lineages. The vaunted progress of life is really random motion away from simple beginnings, not directed impetus toward inherently advantageous complexity.
6. The only promising way to smuggle progress back into such a system is logically possible, but empirically false at high probability. My argument for the whole system is sound: from a necessary beginning at the left wall, random motion of all items in a growing system will produce an increasingly right-skewed distribution. Thus, and with powerful irony, the most venerable evidence for general progress—the increasing complexity of the most complex—becomes a passive consequence of growth in a system with no directional bias whatever in the motion of its components.
But one potential (though much vitiated) argument for general progress remains. The entire system is free to vary only in the direction of greater complexity from an initial position next to the left wall. But what about a smaller lineage that begins at some intermediary position with freedom to expand in either direction (the first living thing starts at the left wall, but the first mammal, or the first seed plant, or the first clam, begins in the middle and its descendants can move toward either tail). If we studied all the smaller lineages free to vary in any direction, perhaps we would then detect a clear bias for net movement to the right, or toward greater complexity. If we found such a bias, we could legitimately speak of a general trend to greater complexity in the evolutionary history of lineages. (This more subtle position would still not explain the general pattern of Figure 29, which would still arise as a consequence of random motion in a growing system constrained to begin at the left wall. But a rightward bias in individual lineages would function as a "booster" or "helpmate" in the general production of right skew. The entire system would then be built by two components: random motion from the left wall, and a rightward bias in individual lineages—and the second component would provide an argument for general progress.)
