E=mc2 (25 page)
Authors: David Bodanis

It usually helps in getting a feel for an equation to "tweak" it by examining its properties at various extreme values. If v is much less than c—i.e., if the shuttle is moving slowly—then (1—v
2
/c
2
) is almost the same as one, for v
2
/c
2
will be so slight. It doesn't matter if you then go on to take its square root and the inverse: you'll still get a number extremely close to 1. For the actual space shuttles launched from Florida, maximum v is about 18,000 mph. That's such a small percentage of the speed of light that its mass only expands by much less than a thousandth of a percent, even when it's screaming out of the atmosphere at top speed. But if a shuttle or anything else is moving really fast, so that v is close to c, then (1—v
2
/c
2
) is close to zero. That means the square root
is
small also, and when you divide 1 by a small fraction, the result is huge. Watch an object streak past at 99 percent of the speed of light—and its mass will to you have increased several times.
There's a temptation to think this is just some quirk, and that although we might be confused in our measurements, a moving object won't "really" be more massive in any way that counts. But the magnets around the accelerator rings at CERN really do have to raise their power this much to keep a proton speeding at that rate on track, for otherwise the momentum of its increased mass will send it into the accelerator's walls. At 90 percent of the speed of light, the power needed
to
control 2.5 times more mass will have to be pumped in to avoid a skid out of the flight path and a crash. If the speed goes up to 99.9997 percent of the speed of light, then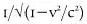 gives a mass increase of 430 times—whence the problems of the accelerators at CERN, having to find some way of drawing their extra energy, without disturbing the good citizens of Geneva.
gives a mass increase of 430 times—whence the problems of the accelerators at CERN, having to find some way of drawing their extra energy, without disturbing the good citizens of Geneva.
Simply to assert, however, that the expression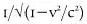 gives a rule you must follow, would put us in the same category as the obedient rule-following instructors Einstein had so resented. At davidbodanis.com we'll explore
gives a rule you must follow, would put us in the same category as the obedient rule-following instructors Einstein had so resented. At davidbodanis.com we'll explore
why
it's true.
Energy that's pumped [in] . . . will turn into extra mass: The shuttle example is only heuristic; we'll see as the book goes on that energy
is
mass: the unified thing called "mass-energy" just happens to take on different aspects, depending on how we're viewing it. The restrictions of our fragile bodies means that we hardly ever change our speeds substantially, and so we view mass from a highly "skewed" angle. That distortion is the reason the "released" energy seems to be so high. (A significant proviso, however, is that this equivalence between mass and energy only holds when an object is viewed from the one particular view in which it's at rest. This is especially important in general relativity, for an object's gravitational attraction stems from its total energy, and not just from its rest mass. Page 199 of the main text touches on this reasoning in connection with black holes; the point is developed at more length on our Web site.
6.
2
"Supervising the workers":
Voltaire et la Societe Francaise au XVIII e Siecle: Volume I, Lajeunesse de Voltaire,
by Gustave Desnoiresterres (Paris: Dider et Cie, 1867), p. 345.
. . . a new concept in the air . . . : Arouet didn't need Newton's work to make him aware of France's faults. If anything, it wasn't abstract ideas, but seeing England's working parliament—and the tradition of at least semi-independent judges and citizens' rights—which helped in showing up the lackings in France. But it was sweet to have the backing of the world's most-renowned analytic system in these critiques. See Voltaire's
English Letters.
Newton had created a system of laws . . . : Curiously enough, seeing an apple fall does seem to have helped Newton take the final step. William Stukeley recorded the elderly Newton reminiscing in his account published two centuries later as
Memoirs of Sir Isaac Newton's Life
(London: Taylor & Francis, 1936), pp. 19-20.
After dinner, the weather being warm, we went into the garden [of Newton's last residence, in London's Kensington] and drank thea, under the shade of some appletrees, only he and myself Amidst other discourse, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. It was occasion 'd by the fall of an apple, as he sat in a contemplative mood. Why should that apple always descend. . . constantly to the earths centre? Assuredly, the reason is, that
. . .
there must be a drawing power in matter . . . like that we here call gravity, which extends its self thro' the universe.
That was how Newton could be so sure that the forces on Earth are the same as those operating up in space. It's easy enough to measure the speed at which an object on Earth falls. In a single second, a dropped apple—or any other object—will fall about 16 feet. But how to measure the speed at which the moon "falls" to compare with that?
The way to do this is to recognize that the moon constantly falls downward, at least a little bit. (If it didn't fall, and only moved in a perfectly straight line, then it would soon shoot away from our planet.) The amount that it "falls" is just enough to keep it curving around the earth. Knowing the length of its orbit, and the amount of time it takes to make one circuit, one can conclude that the moon is tumbling earthward at about 1/20 inch every second.
At first that seems like a failure of Newton's guess. If there's some force making rocks fall 16 feet in one second down on Earth, then one might think that only a very different sort of force, out in distant space, would make giant rocks such as the moon fall a scant 1/20 inch in every second. Even taking into account the greater distance of the moon, it doesn't seem to work. The Earth is about 8,000 miles thick, so Newton, as well as his mother's apple trees, existed about 4,000 miles above the center of the Earth. The moon is in orbit about 240,000 miles from the center of the Earth, i.e., about 60 times farther. Even if you weakened a rock's fall by 60 times, it would still not flutter downward as slowly as the moon. (1/60 of 16 feet is about 3 inches—still far more than the scant 1/20th inch the moon falls each second.)
But what if you imagine a force that weakened by 60
times
60 times as it stretched up and away from our planet? It's an interesting idea—that gravity acts in accord with the square of the distance between objects—but how could you verify such a thing? You would have to prove somehow that gravity produces a force 3,600 times (60 x 60) stronger on Earth than out in space. No one in the seventeenth century— not even from Cambridge—could rocket up to the moon and compare the force of gravity there with what it is on Earth. But no one needed to. The power of equations is immense. Newton had the answer all along. "Why should that apple," he'd asked, "always descend . . . constantly to the earths centre?" In one second on the Earth's surface, a rock or an apple or even an astonished Cambridge don will fall 16 feet. But the moon in that time will fall just 120th inch. Divide the two numbers, and you have the ratio: how much stronger gravity's tugging power is on the Earth's surface than up on the moon.
It's just about 3,600 times.
That was the calculation Newton did, pretty much, in 1666. Imagine a giant clock, where the moon and earth were parts. Newton's rule showed, exactly, how the invisible connecting cogs and rods held the whole swirling contraption together. Anyone reading Newton, and following this argument, could gaze up and understand, for the first time, that the tug of gravity on their body was the same force that reached up, stretching on to the orbit of the moon and forever beyond.
"My youngest flaunts her mind . . .": Samuel Edwards,
The Divine Mistress
(London: Cassell, 1971), p. 12.
. . . memorize cards at the blackjack table: But even this, in her family's opinion, was something she got wrong. "My daughter is mad," her father wrote in exasperation. "Last week she won more than two thousand gold louis at the card tables, and after ordering new gowns . . . she spent the other half on new books She would not understand that no great lord will marry a woman who is seen reading every day." Ibid., p. 11.
"I was tired of the lazy, quarrelsome life . . .": Voltaire's
Memoires;
in Edwards,
The Divine Mistress,
p. 85.
"is changing staircases into chimneys . . .": Letter from Voltaire to Mme de la Neuville, in Andre Maurel,
The Romance of Mme du Châtelet and Voltaire,
trans. Walter Mastyn (London: Hatchette, 1930).
. . . he discovered her with another lover . . . putting him at ease . . . : The various accounts—by servants as well as participants—of this incident are compared in Rene Vaillot's
Voltaire en son temps: avec Mme du Châtelet 1/34-1/48,
published in French by the Voltaire Foundation, Taylor Institution, Oxford England 1988.
The occasional visitors from Versailles . . . : The most thorough description is from Mme de Graffigny's
Vieprivee de Voltaire et de Mme de Châtelet
(Paris, 1820).
She knew that most people felt energy . . . : The word
energy
is anachronistic here, for we're describing the period when these concepts were still being formed. But I think it captures the underlying ideas of the time. See, e.g., L. Lau-dan, "The
vis visa
controversy, a post mortem,"
Isis, 59
(1968), pp. 131-43.
Along with various abstract geometric arguments . . .: Galileo had found that freely tumbling objects don't fall at an unchanging rate. Instead of covering a fixed amount of distance each second, they'll cover 1 unit of distance in the first second, 3 units in the second, 5 units in the third, and so on. Add that sequence of odd numbers together, and you get the
accumulated
distance a falling object travels: In the first second it's 1 unit, in the second it's 4 units (1 + 3), in the third second it's 9 units (1 + 3 + 5), etc. Through a mix of theory and experiment, this was the basis of Galileo's famous result, that accumulated distance is proportional to the square of the amount of time an object's been falling, or d ?t
2
. Leibniz extended this reasoning.
"According to [Newton's] doctrine . . .": Richard West-fall,
Never at Rest: A Biography of Isaac Newton
(Cambridge: Cambridge University Press, 1987), pp.
777-78.
. . . for du Châtelet it was one of the peak moments of her life . . . : The issue is more complex than either Newton or Leibniz recognized, and it took the impartial du Châtelet to understand what was valid and had to be preserved in both. Newton really did have a good point, despite Leibniz's mocking, for if the stars were spread randomly, why shouldn't gravity simply make them fall towards each other? And Leibniz also had a good point, for he never asserted that there was a perfect interventionist God, but merely that there was an optimal deity, subject to constraints we might not be able to see. This was a very different matter. Voltaire missed the point in his powerful satire
Candide, hut it
became a fundamental principle in physics. In a variant form, it became central to Einstein's general relativity, where—as we'll see in the epilogue—planets and stars move in optimal paths within the curved spacetime of the universe.
What effect did it have on Voltaire to see du Châtelet puzzling through these issues? He would constantly be reminded of the contrast between the vast universe and the little "atom of mud" on which vain humans existed—which was one central theme in his work. He would also constantly be reminded of the need to give space for individual genius—a theme that life with the exhausting, exhilarating du Châtelet would no doubt tend to reinforce.
Willem 'sGravesande: The last name is not a misprint; the symbol '5 means "of the" and is still common in Dutch: The city Den Haag (The Hague) is officially called 's-gravenhage (the hague of the Earls). I'm simplifying a large range of experiments 'sGravesande carried out: He used bullet-shaped ivory cylinders, hollow and solid brass balls, pendulums, scraped clay (of deeply elaborate consistency), supporting frames, and a Laputian-like variety of other contraptions to carry out his contention that "The Properties of Body cannot be known
a priori;
we must therefore examine Body itself, and nicely consider all its Properties . . ." See his (most beautifully illustrated)
Mathematical Elements of Natural Philosophy, Confirm'd by Experiments,
trans. J. T. Desaguilliers, especially Book II, ch. 3, 6th edition (London: 1747); the quote is from p. iv.
