E=mc2 (24 page)

The trial itself was on May 8: It's common to read that when Lavoisier was condemned to death, the presiding judge declared, "The Revolution has no need for savants." But it's very unlikely that the president of the court, Jean-Bap tiste Coffinhal, ever said that. The trial was not of individuals, but of the full group of senior members of the General Farm; Lavoisier was not singled out. Fairly detailed accounts of the proceedings survive. What infuriated the court and the jury—which included a barber, a stagecoach employee, a jeweler, and the former Marquis de Mont-fabert, now known simply as Dix-Aout (August 10)—was the way the tax farmers had used their position to extort profits. Many scientists thrived during the Revolution, or at least survived by staying relatively quiet at the various interludes when passions were highest: Carnot, Monge, Laplace, Coulomb, and others. (The phrase "no need for savants" seems to have been invented two years later in a eulogy read by Antoine Fourcroy, a one-time student of Lavoisier's who'd become caught up in Revolutionary enthusiasm and now was trying to backpedal, showing that by all means he hadn't been cowardly in standing aside when his former mentor was attacked.)

"was led to the scaffold in a pitiful state": The witness was Eugene Cheverny, in Poirier,
Lavoisier,
p. 381.

Breathing was more of the same: With such insights, Lavoisier also became the founder of modern biology, by opening up the basics of physiology. Human blood, for example, is mostly water, and if you try to mix oxygen into water, not a great deal will stay there. But if you scatter some finely ground-up iron filings into the water, then oxygen you pump in will stick to that iron just as it did in his lab. (Each iron fragment quickly starts rusting, and in doing so pulls in a great number of oxygen molecules, making them stick. The result is that the iron-rich water can hold on to a lot of oxygen.) This is how blood works: it's red for the same reason that the iron-rich clay soil of Georgia is red.

It was the promise of La Mettrie's
L'Homme Machine;
the same rush of optimism led to Lavoisier himself suggesting that in the future it would be possible to look inside the brain and see "the efforts required of someone giving a speech or . . . the mechanical energy spent by . . . a scholar who is writing, or a musician who is composing"— a pretty near description of our modern brain scans. The quote is from Lavoisier's
Collected Works,
vol. II, p. 697.

This is what Einstein was taught . . . different topics: The division of reality into two parts is something of a default operation of the human mind, seen in the ease with which we create the categories of friend or foe, right or wrong, x or not-x. The particular division bequeathed by Lavoisier, Faraday, and their colleagues was even more compelling, for when one of the divisions is material and physical, and the other is invisible yet still powerful, it's the ancient dichotomy of the body versus the soul that slips into our mind.

Many other thinkers have been guided in their work by that distinction. Alan Turing seems to have been led by the body-soul division when he came up with his distinction between software and hardware; most users of computers easily think that way, for we can all immediately grasp the notion of a "dead" physical substrate, powered up by a "live" controlling power. The soul-body distinction permeates our world: it's Don Quixote versus Sancho Panza; the cerebral Spock versus the stolid
Enterprise;
the contrast between the whispered encouraging voice-overs in the running-shoe ads, and the physical body on the screen.

But these lulling categories only make a suggestive division, not a proof. A young man such as Einstein, always keen to understand the foundation of a field for himself, could readily see that his professors had simply made an induction from a very incomplete data set.

There are many accounts of how lurking categories pull our thoughts along, as with George Lakoff and Mark Johnson's
Metaphors We Live By
(Chicago: University of Chicago Press, 1980), or Kedourie's excellent writings on nationalism, yet for some reason this author is especially pulled toward the approach in Bodanis's
Web of Words: The Ideas Behind Politics
(London: Macmillan, 1988).

. . . when members . . . in Florence: Galileo's proposal was in the First Day section of his
Two New Sciences.
The test was over twenty years later, probably around 1660, by the Accademia del Cimento in Florence. Their results are on page 158 of a book with the sort of vivid identifying location publishers no longer have:
Essayes of Natural Experiments, made in the Academie del Cimento;
Englished by Richard Waller, Fellow of the Royal Society, London. Printed for Benjamin Alsop at the Angel and Bible in the Poultrey, over-against the Church, 1634.

5. c Is for celeritas

The effort might be exhausting . . . embarrassing public exposure: Clearly I'm being slightly tongue in cheek about Cassini. From the available evidence, he might have been an insecure man, but as a newcomer to France he had a great deal to be insecure about: At first his appointment was only temporary, and he'd been warned not to try speaking French, but then he'd been told he
had to
learn French, for the Academy of Sciences couldn't be sullied by being exposed to Latin, let alone his native Italian. It's touching to read his own account of fearfully concentrating to try to develop the crucial language ability—and then his pride when complimented by the king on how much he'd progressed in just a few months. He also had a personal reason to resent Roemer. For Cassini himself had established his reputation by publicly proclaiming, back in July 1665, improved predictions for the transit of Jupiter's satellites. His predictions had been proven right in August and September of that year; his doubters had been humbled; the grand position in Paris had been his reward. He would not have appreciated Roemer trying to use the same twist against him.

There was also something more than mere pique in his critiques of Roemer for being so confident of the Jupiter observations. Cassini wrote a long poem, "Frammenti di Cosmografia," expressing his humility before the grandeur of space, and his belief that only an unjustified false pride lets humans, isolated on one inconsequential planet, presume they can accurately measure everything that occurs. Even before Roemer arrived, Cassini had applied first-order approximations to try to get rid of Io's anomalies; he was being sincere when he said it would be overhasty to insist on any one new interpretation. The poem and fragmentary autobiography are in
Memoires pour Servir a THistoire des Sciences et a Celle de L'Observatoire Royal de Paris
(Paris, 1810), compiled by Cassini's great-grandson, also named Jean-Dominique; see especially pages 292 and 321.

once the underlying mathematics . . . could describe: Maxwell's later success has meant that other researchers of the time have tended to be overlooked. Weber at Gottingen is an especially interesting intermediate figure, for he too computed the speed of light in his efforts to link electricity and magnetism; but as it was masked by an extra factor of v
²
, he didn't recognize what he'd found, and left it aside. Weber's story is nicely described in M. Norton Wise's article "German Conceptions of Force . . . ," pp. 269-307 in
Conceptions of Ether: Studies in the History of Ether Theories 1740-1900, ed.
G. N. Cantor and M. J. S. Hodge (Cambridge: Cambridge University Press, 1981). Weber's caution is similar to that of the early Ampere; his hybrid equations—extending almost into the Maxwellian world of fields, but not quite making it—resemble a battleship forlornly loaded with antiaircraft guns.

"Aye, I suppose . . .": I fear this one is apocryphal too. All that's certain is that Maxwell liked making fun of his own literalness; also that he did experiment with staying up extremely late as a Cambridge student, to the astonishment and bemusement of his fellow students. See e.g., Goldman,
Demon in the Aether,
p. 62.

"They never understood me, but . . .": Ivan Tolstoy,
James Clerk Maxwell: A Biography
(Edinburgh: Canongate, 1981), p. 20.

"As I proceeded with the study . . . " :
Treatise on Electricity and Magnetism,
James Clerk Maxwell (Oxford: Clarendon Press, 1873); Maxwell's preface to his first edition, p. x.

When a light beam starts going forward . . . : Ordinary language is inherently inexact here, for what we're really describing are the properties of electrical and magnetic
fields,
a specification of what "would" happen at any given location. The subjunctive mood in grammar, and especially the subjunctive conditional, comes close to matching the idea: you might not be able to say what's happening at a particular street corner in a bad neighborhood right now, but you could tell what's liable to happen if a Rolex-laden tourist sauntered past. In the case of physics, think of the swirling curves of iron filings you can see around a bar magnet. Now take away those filings, and instead, where each one was, write down a number or a group of numbers that tell you how any filing placed there is likely to respond.

To someone who hadn't seen how you started, there would only be a cold list of numbers. But to someone who knew about the whirling power a magnet can have on iron filings, your list is a vivid description—and to Maxwell and Faraday, with their religious beliefs, your list would be a direct readout of the holy power that created that field in the first place.

The electricity and magnetism . . . "mutual embrace": It doesn't take much power to send out a wave. Play a piano key and the string simply vibrates back and forth, otherwise unmoving, while it's the
pattern
of those vibrations that moves along and carries the sound. There can be hundreds of gallons of air between two people standing a few yards apart in a corridor, yet they don't have to blow all that air forward to call out a hello. Each need only puff the tiny amount that can be shot up from their throats, and that will start a rippling compression wave that gets the job done.

Light and electromagnetic waves generally can be as easy. Switch on the ignition of your car, and your spark plug sends out an electromagnetic wave that has several frequencies that will pass through the metal around it and make it streak to the orbit of the moon within two seconds of your hearing the engine catch; the wave continues outward and will have reached the distance of Jupiter a few hours later.

Maxwell's equations: Maxwell's work was a tremendous achievement—and would have been even more tremendous if he had ever written the four equations that bear his name. But he didn't. It's not just a matter of notation changing, for even the details Hertz later looked at, which led to the realization that radio waves could be transmitted and received like light waves, weren't in the equations Maxwell conceived.

The story of how Maxwell's equations were finally completed, by a group centered around three physicists in England and Ireland in the two decades after his death, is thoroughly recounted in Bruce J. Hunt's
The Maxwellians
(Ithaca, N.Y.: Cornell University Press, 1991).

. . . nothing can
go
faster: Or more precisely, nothing which started slower than the speed of light can end up going faster. What if there were particles—or perhaps an entire parallel world—located permanently on the "other side" of the light speed barrier? It sounds like science fiction, but physicists have learned to keep an open mind. (These postulated superluminal particles were labeled
tachyons
by Gerald Feinberg.) Another proviso is that we're discussing the speed of light in a vacuum, and light's velocity is lower in other substances. This is why diamonds sparkle: light skimming above the surface will go faster than the light that has dipped inside.

There are more significant exceptions—due to the effects of varying space-time curvatures on relative speeds; also there can be effects due to the role of negative energy, and there have also been intriguing results about pulses of light that exceed our velocity "c" (albeit in ways that keep added information from being transferred in the process). These, however, take us beyond the technical level of this book. I suspect future scientists will either look back at us in amazement that we ever took this seriously—or that we took so long to
realize
that this was the way to open up the first Disneyland in Andromeda.

. . . the solid mass of the shuttle starts to grow: None of our ordinary words apply well to this realm, and the term
swelling
has to be thought of as only a metaphor. The shuttle—or a proton, or any other object—doesn't get fatter in all directions. Rather, this is where the seemingly fussy distinction between conservation of matter and conservation of mass from the Lavoisier chapter comes into its own. With mass defined as the property of resistance to an acceleration— which is what we reflexively try to assess whenever we heft an object, to estimate its weight—then it's possible for mass to increase without matter swelling outward. So long as there is an increased resistance to an applied acceleration, the requirements are fulfilled.

In the slow speeds and ordinary realms we're used to, the amount of mass increase will not be enough to notice— this is why Einstein's predictions were so startling—but as an object moves away from us at rates approaching the speed of light, the effect gets clearer. The predictions are very precise.

The way to compute how much a given mass will increase is to take its velocity, square that, divide it by the square of the speed of light, subtract the result from 1, take the square root
of that,
then take the inverse, and then multiply that final result by the mass you're interested in. It's easier in shorthand: if a mass is traveling at the speed of "v," then to work out how much it will appear to swell, you multiply the original mass "m" by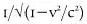
.