Chances Are (5 page)
Authors: Michael Kaplan

Descartes' other vital contribution was separating the physical from the spiritual. As long as the final answer to “Why?” was “God so wills it,” theology governed every question asked about the worldâas Galileo found to his cost. Descartes' mathematics shaped a new dispensation. His graph gives us a means to approximate ever more closely the true qualities of the curve of a functionâbut any two points we plot on a graph, no matter how close together, have an infinity of points between them; we approach but can never reach perfection. Since God is perfect and infinite, we cannot comprehend Himâbut our God-given reason is ample for understanding His creation. All speculation about the physical world becomes permissible because, in the opposed rhythm of speculation and doubt, we progressively refine our concepts toward the vivid, the clear, and the distinct. The more crystalline our ideas, the more closely we approach Divine Truthâalthough we can no more reach it than we can plot every point in a line.
Â
Blaise Pascal was a man in whom the multidimensional contradictions of the medieval mind lined up along the great divide that still marks our way of thought: reason versus faith, rigor versus intuition, head versus heart. Young, startlingly intelligent, well off and well connected, sprightly in speech with a Wildean taste for paradox (“I have made this letter a rather long one, only because I didn't have the leisure to make it shorter”), Pascal personified the cast of mind at which the French excelâand for which their word
esprit
remains the best description.
esprit
remains the best description.
But the spirit was also a source of torment to Pascal: “Fire, Fire, Fire . . . Jesus Christ . . . I have fled Him, renounced Him, crucified Him...” This is part of Pascal's record of an experience of ecstatic devotion on the night of November 23, 1654, preserved on a slip of parchment he wore thereafter, sewn inside his coat. Pascal's religion was deep, personal, and overwhelming; so when he said that he desired certainty above all things, he was talking about more than the area within a curveâhe also meant the salvation of his eternal soul. Not for him Descartes' calm division between worldly doubt and divine faith; the abyss into which every believer must launch himself gaped painfully within his heart.
Of the three intellectual feats that together make Pascal the “father of modern probability”âhis Wager, De Méré's problems, and the Triangleânone was, in fact, original with him. They were all well-known puzzles and curiosities, dating back hundreds of years. Pascal's real accomplishment was to transform each of these attractive mental exercises into the mathematical language of proof.
The question in the Wager is whether to accept faith in God, despite our inability to comprehend Him:
A game is being played at the far end of this infinite distance; heads or tails will turn up. What will you bet? By reason, you can do neither one thing nor the other; using reason, you can defend neither . . . but you must bet. It is not up to you. You are committed. What do you choose, then?
Â
At this point, most previous discussions of faith would become qualitative, explaining that it is not
so
hard to believe, and that Hell is very unpleasant, and eternity extremely long. Pascal remains judicious, expressing the problem as one of expectation, very much in Cardano's terms: “Let us see. Since there is an equal risk of gain and of loss, if you had only to gain two lives, instead of one, you might still wager.”
so
hard to believe, and that Hell is very unpleasant, and eternity extremely long. Pascal remains judicious, expressing the problem as one of expectation, very much in Cardano's terms: “Let us see. Since there is an equal risk of gain and of loss, if you had only to gain two lives, instead of one, you might still wager.”
A modern gambler might set up the problem like this:
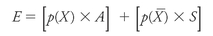 where
where
p
(
X
) is the probability that
X
will happenâin this case, that your faith will save your soulâand
A
is the amount promised to winners.
2
E
is expectation, what you could hope to gain for your stakes; and in this case, you bet your life.
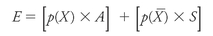
p
(
X
) is the probability that
X
will happenâin this case, that your faith will save your soulâand
A
is the amount promised to winners.
2
E
is expectation, what you could hope to gain for your stakes; and in this case, you bet your life.
Pascal says that, since we have no way of knowing God, we can assume equal probabilities of winning and losing, so
p
(
X
) = 1/2. At these odds, you need to be offered only two lives to make the game fair; if three were offered, you'd be a fool not to bet on God's side.
p
(
X
) = 1/2. At these odds, you need to be offered only two lives to make the game fair; if three were offered, you'd be a fool not to bet on God's side.
But if faith actually
does
save your soul, there is “an infinity of an infinitely happy life to gain.” Since the payoff stands in relation to the stake as the infinite to the finite, you should always bet on God, whatever the odds against you: “There is nothing to decideâyou must give everything.”
does
save your soul, there is “an infinity of an infinitely happy life to gain.” Since the payoff stands in relation to the stake as the infinite to the finite, you should always bet on God, whatever the odds against you: “There is nothing to decideâyou must give everything.”
The popular summary of Pascal's Wager is “Bet on Godâif He exists, you win; if He doesn't, you don't lose anything.” Pascal was not so cynical; for him, the calculation genuinely expressed a belief that probability can offer a handle on the unknown, even if that unknown were as great as the question of our salvation.
Â
The Chevalier de Méré was not simply a high-living gamester but also a capable mathematician. The first problem he brought to Pascal was this: he knew that there is a slightly better than even chance of throwing at least one six in four throws of a die; adding a second die to the throw should simply multiply the number of possible outcomes by sixâso, throwing two dice, shouldn't there be a better-than-even chance of getting at least one double-six in 24 throws? But gamblers were noticing that double-six showed up slightly
less
than half the time in 24 throws. De Méré, Pascal wrote, “was so scandalized by this that he exclaimed that arithmetic contradicts itself.”
less
than half the time in 24 throws. De Méré, Pascal wrote, “was so scandalized by this that he exclaimed that arithmetic contradicts itself.”
Pascal, of course, could not accept such an insult to mathematics; his solution followed the path we have already explored with Cardano. The chance of throwing at least one double-six in 24 throws is the inverse of the chance of
not
throwing a double-six (whose probability is 35/36) in
any
of 24 throws; we can swiftly calculate it as:
not
throwing a double-six (whose probability is 35/36) in
any
of 24 throws; we can swiftly calculate it as:
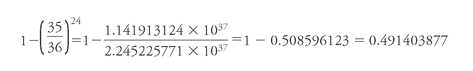
That is, a bit less than 1/2. Pascal, without mechanical help, had redeemed the accuracy of arithmetic: the shooter who bets on making a double-six will lose over time on 24 throws, and will win on 25âjust as the gamblers had found.
De Méré's second problem, the “problem of points,” is deceptively simple. Let's say you and a Venetian have put your stakes on the table; the first to win a certain number of games will pocket the lot. Unfortunately (and here it's tempting to think of some Caravaggio painting of low-life suddenly interrupted by an angel), the game is stopped before either of you has reached the winning total. How should the pile of money on the table be divided?
Fermat (of the Theorem), with whom Pascal discussed the problem, chose a method that adds the probabilities of mutually exclusive events. Let's say the game is to throw a six in eight throws; you are about to roll the first time whenâbehold!âradiance fills the darkened tavern and we are called to higher things. But the money; we can't just leave it there. Well, you could have made the point on your first roll; you had a 1/6 chance of that, so take 1/6 of the pot. But, alternatively, you
could
have failed on the first but made it on the second, so take 1/6 of the remainder, or 5/36 of the total. Then there's the third throwâa further 25/216; and the fourth; add another 125/1296 . . . and so on eight times, adding probabilities and hoping at each stage that someone will have the correct change.
could
have failed on the first but made it on the second, so take 1/6 of the remainder, or 5/36 of the total. Then there's the third throwâa further 25/216; and the fourth; add another 125/1296 . . . and so on eight times, adding probabilities and hoping at each stage that someone will have the correct change.
Fermat was really interested in the problem only as a mathematical construct, but adding up cases of possible success, as Fermat does, can rapidly become a matter of argument: for instance, if you
had
made your point on the first throw, you would not have bothered with the others; why, therefore, should you get anything for them? For Pascal, though, the problem centered around expectation and justice, so his approach was different. He reasons from the money backwards. Let's say the game is one of even chances, like flipping a coin, and you've agreed that the first player to win three games gets the stakes; when the angel appears, you have won two games, your shady opponent one. You could figure the division like this: “There are 64
pistoles
on the table. If I had won this next game, they would all be mine; if I had lost, we would be tied and could divide the pot evenly, 32 each; these two likelihoods are equal, so fairness dictates that I split the difference between 64 and 32 and take 48.” The Venetian pockets his 16 with a suppressed oath, but he cannot fault your logic.
had
made your point on the first throw, you would not have bothered with the others; why, therefore, should you get anything for them? For Pascal, though, the problem centered around expectation and justice, so his approach was different. He reasons from the money backwards. Let's say the game is one of even chances, like flipping a coin, and you've agreed that the first player to win three games gets the stakes; when the angel appears, you have won two games, your shady opponent one. You could figure the division like this: “There are 64
pistoles
on the table. If I had won this next game, they would all be mine; if I had lost, we would be tied and could divide the pot evenly, 32 each; these two likelihoods are equal, so fairness dictates that I split the difference between 64 and 32 and take 48.” The Venetian pockets his 16 with a suppressed oath, but he cannot fault your logic.
Now if you were instead ahead by 2 games to 0 when the game is interrupted, you could extend this reasoning: “If I had won the next game, I would have gained all 64; if I had lost, we would be at 2 games to 1âwhich, as I remember, means I should get 48
pistoles
. So the fair division is halfway between these possibilities: 56 for me, 8 for him.” Once again, you are being as just as Aristotle; and you are free to go out into the deepening evening, the serene city before you and gold jingling in your purse.
pistoles
. So the fair division is halfway between these possibilities: 56 for me, 8 for him.” Once again, you are being as just as Aristotle; and you are free to go out into the deepening evening, the serene city before you and gold jingling in your purse.
So far, so good. But can we figure out a
general
law for interrupted games where you have, say,
r
points still to make and your opponent has
s
? Yes, but to do so we need to take an excursion . . . to the beach, perhaps.
general
law for interrupted games where you have, say,
r
points still to make and your opponent has
s
? Yes, but to do so we need to take an excursion . . . to the beach, perhaps.
Â
Curlews ride the buffeting windâcelestial surfers. The clouds spread in regular ripples like a vast satin quilt. The waves curl, spread, and spring back, as if the ocean were shaking out her hair. Simile reveals patternâone of the deepest human pleasures, a source of excitement and wonder. For Pascal, the mystical prevalence of pattern was evidence of design and spiritual meaning; for scientists, it is an invitation to explore the unknown, promising that the seemingly random has hidden structure.
In art, we play with pattern to make our own significant marks. We can start here, scratching the simplest figure, 1, in the sand. On either side, for symmetry, another 1, thus:
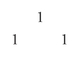
Let's spread these wings a little wider, using a rule (itself a kind of pattern) for filling the space between them: mark down the sum of the two numbers just above to the left and right:
 and so on, filling the sand as we go with our own symmetrical but unexpected design.
and so on, filling the sand as we go with our own symmetrical but unexpected design.

Other books
Iron Eyes Must Die by Rory Black
Dead Man's Embers by Mari Strachan
Red Dog by Louis De Bernieres
Willow by V. C. Andrews
Swimming to Catalina by Stuart Woods
The White Road-CP-4 by John Connolly
Button Holed by Kylie Logan
Tickle His Fancy: Trident Security Book 6 (Trident Security Series) by Samantha A. Cole
Devil's Thumb by S. M. Schmitz
All For You by Kate Perry
