Chances Are (4 page)
Authors: Michael Kaplan

Medieval dice players, honest as well as roguish, must have developed just this sophisticated view of their game. In the mid-thirteenth century, a hundred years before Chaucer's characters danced and diced, a poem appeared called
De vetula
. It is the first text that makes clear the tricky but essential distinction between totals and permutations in dice playing.
De vetula
. It is the first text that makes clear the tricky but essential distinction between totals and permutations in dice playing.
De vetula
describes the 216 possible outcomes from throwing three dice. But waitâbefore you take our word for it,
are
there 216 events? Imagine you have three dice in your hand; look at them for a moment and think about the roll to come. There are sixteen different
totals
that can turn up, from the minimum of three aces to the maximum of three sixesâthat's clear enough. There are also some totals that can be made in different ways: a 9 could be 1 + 3 + 5 or 2 + 2 + 5, for example. How can we calculate the number of sets of numbers that add up to a given total? By starting at the ends and working toward the middle:
describes the 216 possible outcomes from throwing three dice. But waitâbefore you take our word for it,
are
there 216 events? Imagine you have three dice in your hand; look at them for a moment and think about the roll to come. There are sixteen different
totals
that can turn up, from the minimum of three aces to the maximum of three sixesâthat's clear enough. There are also some totals that can be made in different ways: a 9 could be 1 + 3 + 5 or 2 + 2 + 5, for example. How can we calculate the number of sets of numbers that add up to a given total? By starting at the ends and working toward the middle:
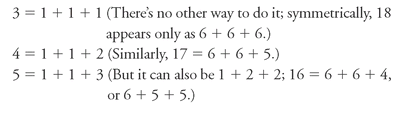
Continue in this vein, adding up the unique throws, or sets of numbers, that produce each total, and you will find that there are only 56 of them. So was
De vetula
wrongâjust another piece of medieval number magic?
De vetula
wrongâjust another piece of medieval number magic?
No, indeed; it established instead a point so subtle that even the great mathematician d'Alembert, author of the article on dice in the
Encyclopédie
of 1751, mistook it:
sequence
is as important as set. 4 = 1 + 1 + 2, but it also equals 1 + 2 + 1 and 2 + 1 + 1. This may seem like pointless wordplay, but you will see its truth if, instead of imagining throwing three dice, you imagine throwing one die three times. In that case, you'd probably agree that these three sequences, although they add up to the same total, are different eventsâespecially if you had a bet riding on one of them.
Encyclopédie
of 1751, mistook it:
sequence
is as important as set. 4 = 1 + 1 + 2, but it also equals 1 + 2 + 1 and 2 + 1 + 1. This may seem like pointless wordplay, but you will see its truth if, instead of imagining throwing three dice, you imagine throwing one die three times. In that case, you'd probably agree that these three sequences, although they add up to the same total, are different eventsâespecially if you had a bet riding on one of them.
Â
Once when I was in Venice, I lost some money at dice; on the following day I lost the rest, for I was in the house of a professional cheat. . . . I impetuously slashed his face with my poignard, though not deeply.
Â
This may not be how most mathematicians now spend their time, but Girolamo Cardano was by no means a typical mathematician.
Born in 1501, the illegitimate son of a prominent Milanese lawyer and scholar, he fought constantlyâagainst poverty, against his own flaws, and, most of all, against Fortune. His eldest son married badly, poisoned his adulterous wife, and was beheaded; his daughter sank into prostitution; his younger son is said to have denounced Cardano to the Inquisition in exchange for the post of public executioner.
There was something obsessive about Cardano: he lists not just his 100 works, published and unpublished, and his 60 “familiar sayings,” but also the 73 times anyone spoke well of him in public. He was intensely interested not only in himself but in the world around him. He took nothing on faithâand here, decades before Galileo, we begin to see the willingness to find and widen little cracks in the shining orb of medieval certainty that would lead, eventually, to what we now call science.
Cardano's mind contained many trains of thought that we would now consider to be on collision courses. There were, he said, three completely different kinds of knowledgeâthe fruits of observation, the results of logic, and divine revelationâand one aspect of his life required all three: gambling. Betting was no mere gentlemanly recreation for Cardano. It was an obsession, and it filled him with shame. Yet he diced for twenty-five years and, through “a certain shrewdness in hazards, and something of skill in play,” he managed to avoid ruin, because he combined logical skill with a sharp eye for the shape of games and a conviction that divinity and chance were different things. His guardian angel might warn Cardano to avoid Mantua, but the dice themselves could tell him the way to bet.
What the dice told him is summed up in his
Liber de ludo aleae (Book of Games of Chance).
This treatise is no piece of academic slumming: it reveals Cardano's mastery of the facts underlying a gambler's instinct. He began with the correct understanding of the number of possible throws with one, two, or three dice: 6, 36, and 216. He called these “circuits” and implied that in an ideal Platonic world, we would see each of the possible throws come up once in a circuit. We mortals are doomed, however, to sit in our cave watching only the shadows of perfection, and so must put up with the fact that in six throws of a die we are unlikely to see the six different points: some will repeat, and some will not turn up at all.
Liber de ludo aleae (Book of Games of Chance).
This treatise is no piece of academic slumming: it reveals Cardano's mastery of the facts underlying a gambler's instinct. He began with the correct understanding of the number of possible throws with one, two, or three dice: 6, 36, and 216. He called these “circuits” and implied that in an ideal Platonic world, we would see each of the possible throws come up once in a circuit. We mortals are doomed, however, to sit in our cave watching only the shadows of perfection, and so must put up with the fact that in six throws of a die we are unlikely to see the six different points: some will repeat, and some will not turn up at all.
At this obvious statement, most previous writers would have signed off with a short cadenza on the inconstancy of fate. Not Cardano: he persists in the idea that if all cases are equally likely, one can expect them to come up in equal proportions,
given enough trials
âif not in one circuit, then in several. He then goes further and states that if, say, 108 of the 216 possible throws of three dice are favorable to your bet, you can expect to win about half the timeâprovided your pockets are deep enough to play a lot of games.
given enough trials
âif not in one circuit, then in several. He then goes further and states that if, say, 108 of the 216 possible throws of three dice are favorable to your bet, you can expect to win about half the timeâprovided your pockets are deep enough to play a lot of games.
Moreover, Cardano was the first to calculate correctly the odds of doing the same thing
more than once:
if the chance of throwing an ace with one die is 1/6, you might think that the chance of throwing a deuce with two dice would be the same. But we have seen that there is only one 2 in the 36 possible outcomes with two dice: the chance of throwing an ace twice in a row is thus 1/6 Ã 1/6, or 1/36; the chance of doing it four times in a row would be 1/6 Ã 1/6 Ã 1/6 Ã 1/6, or 1/1296. This is now known as the “power law”: the probability of repeated successes in several independent trials is calculated by multiplying their individual probabilities.
more than once:
if the chance of throwing an ace with one die is 1/6, you might think that the chance of throwing a deuce with two dice would be the same. But we have seen that there is only one 2 in the 36 possible outcomes with two dice: the chance of throwing an ace twice in a row is thus 1/6 Ã 1/6, or 1/36; the chance of doing it four times in a row would be 1/6 Ã 1/6 Ã 1/6 Ã 1/6, or 1/1296. This is now known as the “power law”: the probability of repeated successes in several independent trials is calculated by multiplying their individual probabilities.
A neat way of illustrating the power law is the old confidence game in which the trickster tips each horse in a ten-horse race to a different group of a hundred mugsâa thousand mugs in all. No matter which horse wins, one group, 1/10 of the total number of mugs, will think: “Hey, this tipster's OK.” The con man then tips each horse in another ten-horse race to groups of 10 from the winning group; one horse wins, and 10 suckers, 1/100 of the original bunch of mugs, will think: “Wow, this tipster's pretty hot.” Tip each horse in the
next
ten-horse race to one of these 10 selected super-rubes and one of them, 1/1000 of the original sample, will conclude: “This tipster's a genius”âand will pay good money for a final, worthless, tip. So to convince one person that you have been right three times at a 1/10 chance, you need 1,000 suckers to begin with:
next
ten-horse race to one of these 10 selected super-rubes and one of them, 1/1000 of the original sample, will conclude: “This tipster's a genius”âand will pay good money for a final, worthless, tip. So to convince one person that you have been right three times at a 1/10 chance, you need 1,000 suckers to begin with:
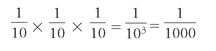
Oddly, Cardano failed to understand the inverse of this reasoning. He was interested, for instance, in how many times you would need to throw a single die to have an even chance of its coming up a six. He felt that since the chance on one throw would be 1/6, then two throws should have twice the likelihood and three throws should produce a probability of 3/6: an even chance.
This reckoning may seem straightforward enough, but it is fundamentally flawed. If, for instance, you extended Cardano's argument beyond six throws, the likelihood of throwing a six would be larger than 1/1: a certainty greater than perfection. What's wrong? The events are
not mutually exclusive:
throwing a six on the first throw does not prevent you from throwing another six on the next. We need to rephrase the question: how many throws produce an even chance of throwing
at least one
six?
not mutually exclusive:
throwing a six on the first throw does not prevent you from throwing another six on the next. We need to rephrase the question: how many throws produce an even chance of throwing
at least one
six?
To answer this, we can perform a neat piece of mathematical inversion; in probability,
at least one
is the opposite of
none:
the chance that something will happen is the inverse of the chance that it will never happen. So if we want to know the chance of throwing a six on the first throw
or
the second
or
the third (and so on), it should be the inverse of the chance of
not
throwing a six on the first throw
and
not on the second
and
not on the third (and so on). That inverse is simple to calculate using the power law, since our chance of
not
getting a six in one throw must be 5/6. Then our chance of not throwing a six in three successive throws is 5/6 Ã 5/6 Ã 5/6 = 125/216 or around 0.5787. This means that the chance of throwing
at least one
six in three throws will be 1â0.5787 or 0.4213. This isn't quite the even chance that Cardano expectedâindeed, it is further off fairness than the house advantage at most casino games. Probability is not an intuitive science.
at least one
is the opposite of
none:
the chance that something will happen is the inverse of the chance that it will never happen. So if we want to know the chance of throwing a six on the first throw
or
the second
or
the third (and so on), it should be the inverse of the chance of
not
throwing a six on the first throw
and
not on the second
and
not on the third (and so on). That inverse is simple to calculate using the power law, since our chance of
not
getting a six in one throw must be 5/6. Then our chance of not throwing a six in three successive throws is 5/6 Ã 5/6 Ã 5/6 = 125/216 or around 0.5787. This means that the chance of throwing
at least one
six in three throws will be 1â0.5787 or 0.4213. This isn't quite the even chance that Cardano expectedâindeed, it is further off fairness than the house advantage at most casino games. Probability is not an intuitive science.
You'll note that Cardano was trying to calculate
even
odds; one characteristic of his analysisâand of all early work on probabilityâis that it is centered around the balance of expectation, not simply the chances of events happening. The problems are posed in terms of the prospects for success or failure in a certain number of attempts, or making a wager that truly reflects the likelihood of an event. One might think this is Cardano as practical gambler, giving the world the first in a long tradition of “beat the casino” handbooks. In fact, the issue is more complicated; and it brings us back to the man whose themes have inspired so many variations in Western culture: Aristotle.
even
odds; one characteristic of his analysisâand of all early work on probabilityâis that it is centered around the balance of expectation, not simply the chances of events happening. The problems are posed in terms of the prospects for success or failure in a certain number of attempts, or making a wager that truly reflects the likelihood of an event. One might think this is Cardano as practical gambler, giving the world the first in a long tradition of “beat the casino” handbooks. In fact, the issue is more complicated; and it brings us back to the man whose themes have inspired so many variations in Western culture: Aristotle.
The
Nicomachean Ethics
has only recently relinquished its claim to underlie all moral philosophy. Indeed, its clarity, radicalism and courageousness in proposing morality without divine sanction suggest that perhaps the claim was given up too soon. Central to the work is
equity
as the desired state: Aristotle is forever proposing ways to establish or maintain fairness in life's relationships. How can we keep friendship with those who are richer, poorer, more intelligent, less beautiful, more influential, less shrewd than ourselves? By exchanging superiorities, giving that of which we are capable in just proportion to what we receiveâeffectively, fitting our wager on the game of life to the odds we live under.
Nicomachean Ethics
has only recently relinquished its claim to underlie all moral philosophy. Indeed, its clarity, radicalism and courageousness in proposing morality without divine sanction suggest that perhaps the claim was given up too soon. Central to the work is
equity
as the desired state: Aristotle is forever proposing ways to establish or maintain fairness in life's relationships. How can we keep friendship with those who are richer, poorer, more intelligent, less beautiful, more influential, less shrewd than ourselves? By exchanging superiorities, giving that of which we are capable in just proportion to what we receiveâeffectively, fitting our wager on the game of life to the odds we live under.
As an Aristotelian, Cardano saw probability not as a science of the behavior of things but as the way to rebalance a world out of kilter, to even the odds so that Fortune becomes what it ought to be: equal chances of equal results, as fair as the flip of a coin. But, Cardano complained, calculating chances in gambling is like trying to understand the significance of supernatural events: “the system comes to naught or is ambiguous.” Caught between ancient authority and modern empiricism, baffled by the distinct but overlapping qualities of the subjects he covered, beaten down by Fortune, and finally silenced by the Church, he slipped the
Liber de ludo aleae
into his strongbox, where it lay forgotten for more than a century.
Liber de ludo aleae
into his strongbox, where it lay forgotten for more than a century.
Â
The healing years pass and the stars wheel by, suggesting in their calm, imperturbable rotation that no idea is lost forever. The decades that followed Cardano's death saw astronomy give to human thought the greatest legacy since consciousness itself: the notion of physical law. The rapid-fire revelations of Copernicus, Galileo, Kepler, and Newton implied that the most fundamental movements of the universe could be not just predicted but explainedâin the clear, unambiguous language of mathematics.
René Descartes (whose belief that staying in bed until noon was essential to the proper working of his brain has made him the hero of every well-read adolescent) gave science both definition and language. Before him, all investigation of the natural world bore the same relation to modern physics that cooking does to chemistry. After him, scientists everywhere could define the scope of their work and reduce it to a form that was transferable and directly applicable to the work of others. Descartes made this possible through two accomplishments: inventing an algebraic geometry and reserving a place for God.
By sliding a grid over a plane, and thus assigning coordinates (
x
,
y
) to every point on that plane, Descartes showed that curves can be written as equations and equations drawn as curves: these two mathematical obsessions are, in fact, one. The pressing geometrical questions in the new astronomy (“What is the area inside this orbit?” “What is the farthest point of this trajectory?”) could now be solved by algebra, the language of equations. Similarly, the behavior of new, exotic equations could become clear through the shapes they revealed as graphs. Pictures were numbers; numbers, pictures. Things seen through eye, telescope, or microscope could be expressed and manipulated with the precision and finality of mathematical proof. It was the end of the medieval sorting of knowledge by qualities.
x
,
y
) to every point on that plane, Descartes showed that curves can be written as equations and equations drawn as curves: these two mathematical obsessions are, in fact, one. The pressing geometrical questions in the new astronomy (“What is the area inside this orbit?” “What is the farthest point of this trajectory?”) could now be solved by algebra, the language of equations. Similarly, the behavior of new, exotic equations could become clear through the shapes they revealed as graphs. Pictures were numbers; numbers, pictures. Things seen through eye, telescope, or microscope could be expressed and manipulated with the precision and finality of mathematical proof. It was the end of the medieval sorting of knowledge by qualities.
Other books
Words Like Coins by Hobb, Robin
Monsters & Fairytales by Rebecca Suzanne
The Wildest Heart by Terri Farley
All Other Nights by Dara Horn
April, Dani - Superstar (Siren Publishing Ménage Amour) by Dani April
Murder in Jerusalem by Batya Gur
One Night with Sole Regret 03 Take Me by Olivia Cunning
Where She Belongs by Johnnie Alexander
Ungrateful Dead by Naomi Clark
Unknown by Unknown
