Call Sign Extortion 17 (18 page)
Read Call Sign Extortion 17 Online
Authors: Don Brown

Now compare this to the diagram shown in the Colt Report. By analogy, point “B” would be the point at which the RPG struck the helicopter blade.

Point “C” is the ground, which is 100 feet below point “B.”
From the diagram in the report itself, the tip of the arrow represents capital “B,” the point of attack.
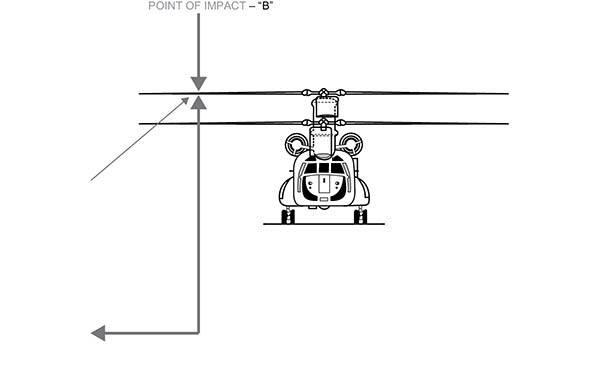
Here the triangle comes together as shown on page 14 of Exhibit 60. The ground under the chopper is capital “C,” called “ground zero,” because this is the point directly under the chopper at the moment of impact.
By extrapolation, and based on the angle of attack shown in the JCAT report, Point “A” would mark the position from which the shots were fired, based upon the angle that the RPG struck.

The distance between Point “A” (origin of shot) and Point “B” (point of impact) runs along the hypotenuse of the triangle. Remember from high school geometry class that the hypotenuse is the longest side of a triangle.
Remember also there's a formula for calculating the distance of the hypotenuse. That's the old Pythagorean theorem, which is a
2
+ b
2
= c
2
, with c as the hypotenuse and a and b as the two shorter sides of the triangle.
In this case, the hypotenuse is going to be the actual distance that the RPG traveled in the air before it struck the blade of Extortion 17.
Look at the model triangle again:

The capital “B” represents the position of the helicopter (Extortion 17). The small “c” is the hypotenuse, and represents the angle and distance that the RPG traveled to strike the helicopter. Also remember that the three interior angles of a triangle must add up to 180 degrees.
Again, the position at capital “C” (ground zero) marks the position on the ground just below Extortion 17 the moment it was struck by the RPG.
The small “a” and the small “b” are the “legs” of the triangle, and the small “a” represents the distance between the helicopter at the point of impact and the ground
, which the Combat Assessment Team determined to be between 100 and 150 feet
(Exhibit 60, page 6).
All triangles have 180 degrees total. In this triangle, the interior angle at Point “C”âground level under Extortion 17 (ground zero), is 90 degrees (a right angle).

That leaves a total of 90 degrees to work with using the remaining interior angles, which are the key to determining the length of leg “b” (distance from shooter to ground zero) and the hypotenuse “c” (distance from shooter to blade of helicopter).
In the diagram provided at page 14 of Exhibit 60, it appears that the interior angles at “A” (position of shooter) and “B” (point of impact) are each about 45 degrees.
Actually, that's not far off. On page 28 of exhibit 60, the interior angle at the point of impact “B” was given as approximately 50 degrees. The report showed that the “
(S) Weapon angle of impact was approximately 40Ë relative to the bottom surface of the blade
” [author's emphasis].
In other words, from the bottom surface of the blade to the line of attack by the RPG (the hypotenuse of the triangle), there was an angle of 40 degrees.
Now the blade, which was spinning horizontally, and the line down to ground zero intersect and form a right triangle of 90 degrees, mirroring the right triangle at ground zero (point “C”).

Let's look at our triangle again.

So to review, the interior angle at “B” (point of impact) is 50 degrees. The interior angle at C (ground zero) is 90 degrees, because it's a right angle. The interior angle at A (position of shooter) is by deduction 40 degrees, because we've already used up 140 degrees (90 at ground zero plus 50 at point of impact) leaving only 40 degrees.
With the length of “a” and the interior angle of “B” (50 degrees), the distance from the shooter to the chopper can be computed using the basic trigonometric principles of sine, cosine, and tangent.
The tangent of 50 degrees is 1.19. Remember that the known height “a” from ground zero (Point C) to the point of impact (Point B) is 100 feet.
To determine distance from ground zero to the shooter (line “b”), multiply 1.19 by 100 (length of “a”). 100 x 1.19 = 119 feet.
So now we know that the shooter was lurking only 119 feet from ground zero, at the time he fired the RPG that brought the chopper down.
Stop and consider this for a moment. Remember that the blades on that chopper were 120 feet all the way across, so that means they extended 60 feet out from the axis.
The shooter, assuming Extortion 17 was at a height 100 feet above ground, was on the ground 119 feet away from ground zero. But the choppers' blades extend 60 feet each way out from the spinning axis being driven by the rear engine. That means that the shooter was so close to the chopper's flight path that he could have been as close as 59 feet to being directly under the rotation of the blade!
That math is easy to calculate. 119 feet distance, shooter to ground zero minus 60-foot radius of the blade, leaves you with 59 feet. That's how close the shooter was to being almost directly under the chopper as it landed.
On August 10, 2011, four days after the shoot-Âdown, the UK
Daily Mail
quoted an Afghan governmental official as saying that the Taliban was tipped off as to the mission, that the Taliban knew the flight path, and that the chopper was lured to the landing zone.
Â
He (an Afghan government official) said that Taliban commander Qari Tahir lured US forces to the scene by tipping them off that a Taliban meeting was taking place.
He also said four Pakistanis helped Tahir carry out the strike.
“Now it's confirmed that the helicopter was shot down and it was a trap that was set by a Taliban commander,” said the official, citing intelligence gathered from the area.
Â
That same report, that the Taliban had knowledge of the flight of Extortion 17, followed in one of the other major British dailies, the UK
Telegraph.
Bear in mind this is not the Taliban crowing. It's the British press quoting the Afghan government.
If the chopper were lured in by baited information on Tahir's location, that would explain how the Taliban got off such a point-Âblank shot. And the math above shows that the shot was about as point-Âblank as you can get, which proves that (a) the
Daily Mail
report that the Taliban was tipped off on Extortion 17's flight plan from the inside was probably correct, and (b) that the position in General Colt's Executive Summary later adopted by the Defense Department, that the RPG was fired from a tower 220 meters (720 feet) away, is mathematically impossible.
Now moving on in our calculations, there's still one number missing, and that's the length of the hypotenuse, or “c,” which will show the actual distance between the shooter and the helicopter. Remember that General Colt claimed 220 meters or 720 feet (beyond the effective range of the RPG).
But now apply the Pythagorean theorem, a
2
+ b
2
= c
2
, to get an idea of just what a point-Âblank shot this was.
