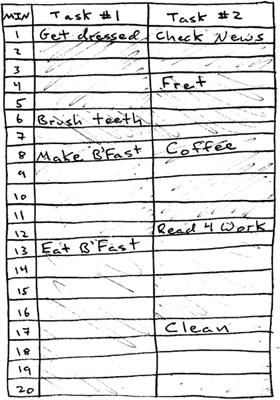
Brain Trust (32 page)
Authors: Garth Sundem

The same is true of absolutely anything—information creates essence, and essence creates pleasure. Does your spouse have a hobby you find completely inane? Learn about it to increase your own pleasure. If you just can’t care about the difference between a Dogfish Head microbrew and Bud Light, take a brewing class. If you want to increase the pleasure of your vacation, learn about a place’s essence—its history and culture.
Using knowledge rather than price to add essence means you can get more pleasure for less money.
Puzzle #18:
Happiness at What Cost?
Jo makes $21.75/hr as a freelance medical transcriptionist. And let it be said that she also likes her wine. Every hour she spends learning about a bottle’s origin (estate, winery, year, etc.) increases her enjoyment as much as buying a bottle half again the price of the first. How much must a bottle cost to make spending an hour learning about the wine a better buy than spending an hour working in order to buy a pricier bottle?
PUZZLE ANSWERS
1. MATH IS TOO SEXY
Start with mat = hematic
• Cancel “mat” leaving: 1 = heic
• Use e = mc
2
to get: 1 = H(mc
2
)IC
• Use U = mgh to get: 1 = (u/mg)(mc
2
)IC
• Simplify: mg = umc
2
IC
• Cancel “m” to get: g = uc
2
IC
• Combine “c” to get g = uc
3
i
• Write as: G = uccci
2. DR. STAT CRICKET PROP
In standard weather, the payout for a wager is the 1/46 chance of winning times the 46 payout, for exactly even money. Over time you break even. But in cold weather, Dr. Stat knows the chance of winning on each throw is 1/46 + 1/100 = 0.032. This times the 46 payout is an expected value of 1.46 times his money with each bet. If he bets $1,000 on one throw, that’s an expected $1,460, and more than one hundred throws, that’s $146,000. Of that total, $1,000 is his original bankroll, so he should expect to win $145,000.
3. MULTITASKING MIX AND MATCH
4. MATCHMAKER
The power pair of Jake and Emma is a red herring. Their bliss would force enough unhappiness on others that it’s not worth allowing this match made in heaven. Instead, the pairs that create the highest overall happiness are John/Ella, Jeremy/Eliza, Jake/Eva, and Justin with the (apparently) effervescent Emma for a total of 51 preference points.
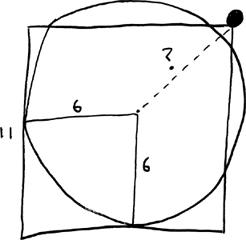
5. TRAMP TROUBLE
The biggest quadrant of the garage is the lower left, which is shown below, with a hypothetical trampoline. The question is, is the dotted line longer than 6 feet? Well, the dotted diagonal is the hypotenuse of a right triangle with sides of 5 feet and 4 feet. So 5
2
+ 4
2
= (Dotted line)
2
and the dotted line is 6.4 feet long. Yes! The tramp will fit! Now let’s hope the door to the house is on the right and not the left side of the garage.
6. RACETRACK
7. DISMEMBERED ZOMBIES
Isn’t it frustrating that you can make a max of only three zombies from all these good parts?
8. BINGO! (SCRABBLE)
Elaters, Realest, Relates, Reslate, Stealer
9. BOOMERANG V. ZOMBIE
This is mostly a problem of conversions. It takes the zombie 6.09 seconds to cover the span (including the 2-second delay). And it would take the boomerang 6.42 seconds to return. If our hero runs, he reaches safety in 6.63 seconds. This looks bad all around, until you realize that the zombie also has to cover the extra distance to the tree, which takes it an extra 1.09 seconds. If the hero runs for the tree, he’ll avoid the unwilling donation of his gray matter. (If you really want to bend your mind, imagine what happens if the hero runs toward the returning boomerang.…)
10. THE GOSSIP WEB
Here is one answer. There might be more.
11. CAKE CUTTING
There are two fair ways to allocate the Batman. First imagine the cake as “points” combining volume with Batman—if B gets Batman, the cake is worth 168 total points, and if A gets Batman, the cake is worth 187 total points. And fair volume is B = 1.5A.
• So in the first case, A + 1.5A = 168. A gets 67.2 “points” of cake, and B gets 100.8 points of cake, of which 8 are due to Batman, so 92.8 in
3
of cake. Cutting the cake lengthwise, A gets a strip 3.36 inches wide, and B gets a strip 4.64 inches wide, including the Batman.
• In the second case, A + 1.5A = 187. A gets 74.8 points, of which 27 are due to Batman, so 47.8 in
3
of cake. B gets 112.2 points, all of which are due to cake. Cutting lengthwise, A gets a strip 2.29 inches wide including Batman, and B gets a strip 5.61 inches wide.
• But check this out: Giving A the Batman she so covets increases the overall value of the cake. And so to create maximum happiness, you should cut the cake so that she gets the Dark Knight, while compensating B with more cake.
12. FRIENDS ADD UP
Grade school = 13; high school = 13; summer camp = 13; college = 15; your first job = 15; grad school = 15; your kids’ friends’ parents = 17; an online fantasy football league = 17; and your current job = 32. 3(13) + 3(15) + 2(17) + 32 = 150.
13. A THREE-HOUR TOUR?
14. SCHOOLED BY FISH
Fish number 2 is a red herring (sorry …). Its personal connections are many but most of them are dead-end friends. Instead, fish numbers 9 and 11 are higher, with number 11’s friends-of-friends-of-friends connections making it the winner, with a score of about 4.
15. TIME DISCOUNTING
The method is outed in the puzzle description—the “worth” of marshmallows at some point in the future is a problem of exponential decay, which uses the following equation:
(Remaining Amount) = (Starting Amount) e
(Decay Rate x Time)
Since marshmallows lose a quarter of their value every three minutes of wait time, 1 marshmallow will be worth only ¾ in
3 minutes. Plug these values into the equation for exponential decay to get this: ¾ = 1e
k3
.
Solve:
• ¾ = e
3k
• ln4/3 = 3k
• k = 0.09589
Now, at what point will the value of five marshmallows equal the value of only one marshmallow (remember, you get four additional marshmallows, making five total)? You can write the equation like this: 1 = 5e
0.09589
t.
Solve:
• 1 = 5e
0.09589
t
• 1/5 = e
0.09589
t
• ln5 = 0.09589t
• t = 16.78 minutes
So the value of eating your initial marshmallow immediately is exactly equal to the value of eating five marshmallows 16 minutes and 47 seconds in the future. If you have to wait 20 minutes for the reward, you’d be better off immediately scarfing your first marshmallow.
Bonus question: How long do you have to make your decision before you’re better off waiting for the additional four marshmallows at 20 minutes?
16. OCTOBER BOY
This is another twist on Martin Gardner’s famous gender problem. Again, combining birth order with gender means with two kids you could have B-B, B-G, G-G, or G-B. Now, imagine the number of distinct possibilities with the calendar:
• If you first have a boy on a day containing a “1,” you could have a boy or a girl second, on any of the 31 days, for a total of 62 possibilities, 31 of which are two boys. Cool.
• And the same is true if you second have a boy on a “1”: 62 possibilities, of which half are boys. Only, 13 of these “new” possibilities aren’t distinct. You already included boy-boy on every day containing a one. So instead of adding 62 more distinct possibilities, this adds only 49 new possibilities, of which only 18 are two boys.
• So add up all the possibilities for two boys: 31 + 18 = 49. And add up all possibilities: 62 + 49 = 111. There’s a 49/111 = 0.44 probability that both kids will be boys.
17. MAP PROBLEM