Alex’s Adventures in Numberland (70 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Gauss’s final contribution to research on the fifth postulate came shortly before he died, when, already seriously ill, he set the title for the probationary lecture of one of his brightest students, 27-year-old Bernhard Riemann: ‘On the hypotheses that lie at the foundations of geometry’. The cripplingly shy son of a Lutheran pastor, Riemann at first had some kind of breakdown struggling with what he would say, yet his solution to the problem would revolutionize maths. It would later revolutionize physics too, since his innovations were required by Einstein to formulate his general theory of relativity.
Riemann’s lecture, given in 1854, consolidated the paradigm shift in our understanding of geometry resulting from the fall of the parallel postulate by establishing an all-embracing theory that included the Euclidean and non-Euclidean within it. The key concept behind Riemann’s theory was the
curvature
of space. When a surface has zero curvature, it is
flat
, or Euclidean, and the results of
The Elements
all hold. When a surface has positive or negative curvature, it is
curved
, or non-Euclidean, and the results of
The Elements
do not hold.
The simplest way to understand curvature, continued Riemann, is by considering the behaviour of triangles. On a surface with zero curvature, the angles of a triangle add up to 180 degrees. On a surface with
positive
curvature, the angles of a triangle add up to
more than
180 degrees. On a surface with negative curvature, the angles of a triangle add up to
less than
180 degrees.
A sphere has positive curvature. We can see this by considering the sum of the angles of the triangle in the following diagram, which is made by the equator, the Greenwich Meridian and the line of longitude 73 degrees west of Greenwich (which goes through New York). Both angles where the longitude lines meet the equator are 90 degrees, so the sum of all three angles must be more than 180. What type of surface has negative curvature? In other words, where are there triangles whose angles add up to less than 180 degrees? Pop open a pack of Pringles, and you’ll see. Draw a triangle on the saddle part of the potato crisp (possibly with some fine French mustard) and the triangle looks ‘sucked in’ compared to the ‘puffed out’ triangle we see on a sphere. Its angles are clearly less than 180 degrees.
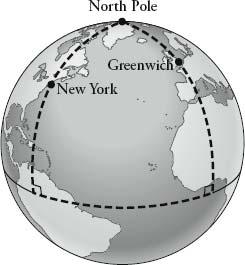
Triangle on a sphere: sum of angles greater than 180 degrees.
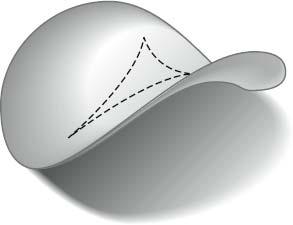
Triangle on a Pringle: sum of angles less than 180 degrees.
A surface with negative curvature is called
hyperbolic
. So, the surface of a Pringle is hyperbolic. The Pringle, however, is only an
hors d’oeuvre
in understanding hyperbolic geometry since it has an edge. Show a mathematician an edge and he or she will want to go over it.
Consider it this way. It is straightforward to imagine a surface with zero curvature and no edge: for example, this page, flattened on a desk, and extended infinitely in all directions. If we lived on such a surface and we started walking in a straight line in any direction, we would never reach an edge. Likewise, we have an obvious example of a surface with positive curvature and no edge: a sphere. If we lived on the surface of a sphere, we could walk for ever and ever in one direction and never reach an edge. (Of course, we do live on a rough approximation of a sphere. If the Earth were totally smooth, with no oceans or mountains to block our way, for example, and we started walking, we would return to our point of departure and continue going in circles.)
Now, what does a surface with negative curvature and no edge look like? It cannot lSo, theike a Pringle, since if we lived on an Earth-sized Pringle and we started walking in one direction, we would always eventually fall off it. Mathematicians have long wondered what an ‘edgeless’ hyperbolic surface might look like – one on which we could walk as far as we wished without coming to the end of it and without it losing its hyperbolic properties. We know it must be always curving like a Pringle, so what about sticking lots of Pringles together? Sadly, this wouldn’t work since Pringles don’t fit together neatly, and if we filled in the gaps with another surface these new areas would not be hyperbolic. In other words, the Pringle allows us to envisage only a local area with hyperbolic properties. What is incredibly difficult to envisage – and stretches even the most brilliant mathematical minds – is a hyperbolic surface that goes on for ever.
Spherical and hyperbolic surfaces are mathematical opposites, and here is a practical example that shows why. Cut a piece out of a spherical surface, such as a basketball. When we squash the piece on the ground to make it flat it will either stretch or rip, since there is not enough material to spread out in a flat way. Now imagine we had a rubber Pringle. When we try to flatten it, the Pringle would have
too much
material and some of it would fold on itself. Whereas the sphere closes in on itself, the hyperbolic surface expands.
Let’s return to the parallel postulate, which provides us with a very concise way of classifying flat, spherical and hyperbolic surfaces.
For any given line and a point not on that line:
On a
flat
surface there is
one and only one
parallel line through that point.
On a
spherical
surface there are
zero
parallel lines through that point.
*
On a
hyperbolic
surface there is
an infinite number
of parallel lines through that point.
We can understand intuitively the behaviour of parallel lines on a flat or on a spherical surface, because we can easily visualize a flat surface that goes on for ever and we all know what a sphere is. It is much more challenging to understand the behaviour of parallel lines on a hyperbolic surface, since it is not at all clear what such a surface might look like as it spreads to infinity. Parallel lines in hyperbolic space get further and further apart from each other. They do not bend away from each other, since for two lines to be parallel they must also be straight, but they diverge because a hyperbolic surface is constantly curving away from itself, and as the surface curves away from itself it creates more and more space between any two parallel lines. Again, this idea is totally mind-boggling, and it’s hardly surprising that, despite his genius, Riemann did not come up with a surface that had the properties he was describing.
The challenge of visualizing the hlic plane galvanized many mathematicians in the final decades of the nineteenth century. One attempt, by Henri Poincaré, caught the imagination of M.C. Escher, whose famous
Circle Limit
series of woodcuts was inspired by the Frenchman’s ‘disc model’ of a hyperbolic surface. In
Circle Limit IV
, a two-dimensional universe is contained on the circular disc in which angels and devils get progressively smaller the closer they get to the circumference. The angels and devils, however, are not aware that they are getting smaller since as they shrink, so too do their measuring tools. As far as the inhabitants of the disc are concerned, they are all the same size and their universe goes on for ever.

Circle Limit IV.
The ingenuity of Poincaré’s disc model is that it illustrates beautifully how parallel lines behave in hyperbolic space. First, we need to be clear what straight lines are in the disc. In the same way that straight lines on a sphere look curved when represented on a flat map (for example, flight paths are straight, but look curved on a map), lines that are straight in the discworld also look to us like they are curved. Poincaré defined a straight line in the disc as being a section of a circle that enters the disc at right angles. Figure 1 overleaf shows the straight line between A and B, which is made by finding the circle that goes through A and B and that enters the disc at right angles. The hyperbolic version of the parallel postulate states that for every straight line L and a point P not on that line, there is an infinite number of straight lines parallel to L that pass through P. This is shown in figure 2, where I have marked three straight lines – L', L' ' and L' '' – that pass through P but are all parallel to L. (Two lines are parallel if they are both straight and never meet.) Each of the lines L', L' ' and L' '' are parts of different circles that enter the disc at right angles. By looking at the disc we can now see how it must be the case that there is an infinite number of straight lines that are parallel to L and that pass through P, since we can draw an infinite number of circles that enter the disc at right angles and pass through P. Poincaré’s model also helps us understand what it means for two parallel lines to diverge: L and L' are parallel but become further and further apart the closer they get to the circumference of the disc.
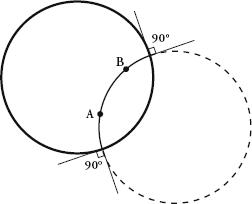
Figure 1

