Alex’s Adventures in Numberland (65 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

The quincunx.
Using probability, we can understand what is going on. First, imagine a quincunx with just one pin and let us say that when a ball hits the pin the outcome is random, with a 50 percent chance that it bounces to the left and a 50 percent chance of it bouncing to the right. In other words, it has a probability of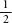 of ending up one place to the left and a probability of
of ending up one place to the left and a probability of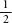 of being one place to the right.
of being one place to the right.
Now, let’s add a second row of pins. The ball will either fall left and then left, which I will call LL, or LR or RL or RR. Since moving left and then right is equivalent to staying in the same position, the L and R together cancel each other out (as does the R and L together), so there is now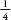 of a chance the ball will end up one place to the left,
of a chance the ball will end up one place to the left,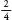 chance it will be in the middle and
chance it will be in the middle and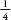 it will be to the right.
it will be to the right.
Repeating this for a third row of pins, the equally probable options of where the ball will fall are LLL, LLR, LRL, LRR, RRR, RRL, RLR, RLL. This gives us probabilities of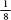 of landing on the far left,
of landing on the far left, of landing on the near left,
of landing on the near left, of landing on the near right and
of landing on the near right and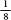 of landing on the far right.
of landing on the far right.
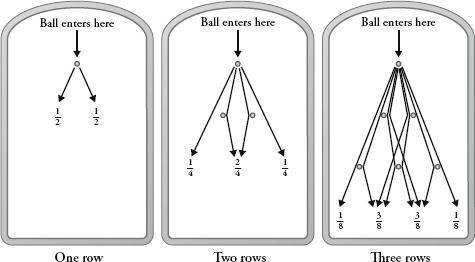
In other words, if there are two rows of pins in the quincunx and we introduce lots of balls into the machine, the law of large numbers says that the balls will fall along the bottom such as to approximate the ratio 1:2:1.
If there are three rows, they will fall in the ratio 1:3:3:1.
If there are four rows, they will fall in the ratio 1:4:6:4:1.
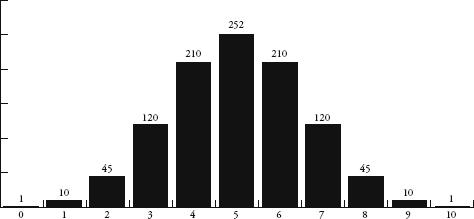
If I carried on working out probabilities, a ten-row quincunx will produce balls falling in the ratio 1:10:45:120:210:252:210:120:45:10:1.
Plotting these numbers gives us the first of the shapes below. The shape becomes even more familiar the more rows we include. Also below are the results for 100 and 1000 rows as bar charts. (Note that only the middle sections of these two charts are shown since the values to the left and right are too small to see.)
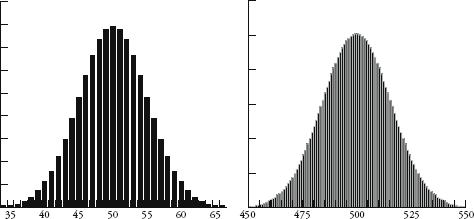
So how does this pinball game relate to what goes on in the real world? Imagine that each row of the quincunx is a random variable that will create an error in measurement. Either it will add a small amount to the correct measurement or it will subtract a small amount. In the case of Galileo and his telescope, one row of pins could represent the temperature of the equipment, another could represent whether there is a thermal front passing through, and another could represent the pollution in the air. Each variable contributes an error either one way or the other, just as in the quincunx the ball will bounce left or right. In any measurement there may be many millions of unobservable random errors – their combined errors, however, will give measurements that are distributed like a bell curve.
