100 Essential Things You Didn't Know You Didn't Know (7 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

If we move up from lines enclosing areas to surfaces enclosing volumes then we face a similar problem. What shape can maximise the volume contained inside a given surface area? Again, the biggest enclosed volume is achieved by the sphere, with a volume V = 4πr
3
/3 inside a spherical surface of area A = 4πr
2
. So for any
closed
surface of area A we expect its enclosed volume to obey A
3
≥ 36πV
2
, with equality for the case of the sphere. As before, we see that by making the surface highly crenellated and wiggly we can make the area enclosing a given volume larger and larger. This is a winning strategy that living systems have adapted to exploit.
There are many situations where a large surface area is important. If you want to keep cool, then the larger your surface area the better. Conversely, if you want to keep warm it is best to make it small – this is why groups of newborn birds and animals huddle together into a ball so as to minimise exposed surface. Likewise, the members of a herd of cattle or a shoal of fish seeking to minimise the opportunities for predators will gather themselves into a circular or spherical group to minimise the surface that a predator can attack. If you are a tree that draws moisture and nutrients from the air, then it pays to maximise your surface area interfacing with the atmosphere, so it’s good to be branchy with lots of wiggly leafy surfaces. If you are an animal seeking to absorb as much oxygen as possible through your lungs, then this is most effectively done by maximising the amount of tubing that can be fitted into the lung’s volume so as to maximise its surface interface with oxygen molecules. And if you simply want to dry yourself after getting out of the shower, then a towel that has lots of surface is best. So towels tend to have a rough pile on their surfaces: they possess much more surface per unit of volume than if they were smooth. This battle to maximise the surface that is enclosing a volume is something we see all over the natural world. It is the reason that ‘fractals’ so often appear as an evolutionary solution to life’s problems. They provide the simplest systematic way to have more surface than you should for your volume.
Is it better for you to stay in one group or to split up into two or more smaller groups? This was a problem faced by naval convoys trying to avoid being found by enemy submarines during the Second World War.
It is better to stay in a big convoy rather than to divide. Suppose that a big convoy covers an area A and the ships are as close together as they can be, so that if we divide the convoy into two smaller ones of area A/2 the spacings between ships are the same. The single convoy has a perimeter equal to p = 2π√(A/π), but the total perimeter of the two smaller convoys equals p×√2, which is bigger. So, the total perimeter distance that has to be patrolled by destroyers to protect the two smaller convoys from being penetrated by submarines is greater than that to be patrolled if it stays as a single convoy. Also, when the submarine searches for convoys to attack, its chance of seeing them is proportional to their diameter, because this is what you see in the periscope. The diameter of the single circular convoy of area A is just 2√(A/π), whereas the sum of the two diameters of the convoys of area A/2 that don’t overlap in the field of view is bigger by a factor of √2, and so the divided convoy is 41% more likely to be detected by the attacking submarine than is the single one.
18
VAT in Eternity
In this world nothing is certain but death and taxes.
Benjamin Franklin
If you live in the United Kingdom you will know that the sales tax added on to many purchases is called ‘Value Added Tax’ or VAT. In continental Europe it is often called IVA. In the UK it amounts to an additional 17.5% on the price of a range of goods and services and is the government’s biggest source of tax revenue. If we suppose that the 17.5% rate of VAT was devised to allow it to be easily calculated by mental arithmetic what do you expect the next increase in the rate of VAT to be? And what will the VAT rate be in the infinite future?
The current value of the VAT rate sounds arcane – why pick 17.5%? But if you have to prepare quarterly VAT accounts for a small business you ought soon to recognise the niceness of this funny number. It allows for very simple mental calculation because 17.5% = 10% + 5% + 2.5%, so you know what 10% is immediately (just shift the decimal point one place to the left), then just halve the 10%, and then halve the 5% that remains and add the three numbers together. Hence, for example, the VAT on an £80 purchase is just £8 + £4 + £2 = £14.
If the same convenient ‘halving’ structure for mental arithmetic is maintained, then the next VAT increase will be by an amount equal to half of 2.5%, or 1.25%, giving a new total
of
18.75% and the new VAT on £80 would be £8 + £4 + £2 + £1 = £15.
We would then have a tax rate that looked like 10% + 5% + 2.5% + 1.25%. To the mathematician this looks like the beginnings of a never-ending series in which the next term in the sum is always half of its predecessor. The current VAT rate is just
10% × (1 + ½ + ¼)
If we continue this series forever we can predict that the VAT rate in the infinite future will be equal to
10% × (1 + ½ + ¼ + ⅛ + +
+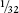 + . . . ) = 10% × 2
+ . . . ) = 10% × 2
where, as we
see here
, the same series except for the first term is shown to sum to 1, so the sum of the infinite series in brackets is 2. The VAT rate after infinite time is therefore expected to be 20% !
19
Living in a Simulation
Nothing is real.
The Beatles, ‘Strawberry Fields Forever’
Is cosmology on a slippery slope towards science fiction? New satellite observations of the cosmic microwave background radiation, the echo of the Big Bang, have backed most physicists’ favourite theory of how the Universe developed. This may not be entirely good news.
The favoured model contains many apparent ‘coincidences’ that allow the Universe to support complexity and life. If we were to consider the ‘multiverse’ of all possible universes, then ours is special in many ways. Modern quantum physics even provides ways in which these possible universes that make up the multiverse of all possibilities can actually exist.
Once you take seriously the suggestion that all possible universes can (or do) exist then you also have to deal with another, rather strange consequence. In this infinite array of universes there will exist technical civilisations, far more advanced than ourselves, that have the capability to simulate universes. Instead of merely simulating their weather or the formation of galaxies, as we do, they would be able to go further and study the formation of stars and planetary systems. Then, having added the rules of biochemistry to their astronomical simulations, they would be able to watch the evolution of life and consciousness within their computer
simulations
(all speeded up to occur on whatever timescale was convenient for them). Just as we watch the life cycles of fruit flies, they would be able to follow the evolution of life, watch civilisations grow and communicate with each other, even watch them argue about whether there existed a Great Programmer in the Sky who created their Universe and who could intervene at will in defiance of the laws of Nature they habitually observed.
Within these universes, self-conscious entities can emerge and communicate with one another. Once that capability is achieved, fake universes will proliferate and will soon greatly outnumber the real ones. The simulators determine the laws that govern these artificial worlds; they can engineer fine-tunings that help the evolution of the forms of life they like. And so we end up with a scenario where, statistically, we are more likely to be in a simulated reality than a real one because there are far more simulated realities than real ones.
The physicist Paul Davies has recently suggested that this high probability of our living in a simulated reality is a
reductio ad absurdum
for the whole idea of a multiverse of all possibilities. But, faced with this scenario, is there any way to find out the truth? There may be, if we look closely enough.
For a start, the simulators will have been tempted to avoid the complexity of using a consistent set of laws of Nature in their worlds when they can simply patch in ‘realistic’ effects. When the Disney company makes a film that features the reflection of light from the surface of a lake, it does not use the laws of quantum electrodynamics and optics to compute the light scattering. That would require a stupendous amount of computing power and detail. Instead, the simulation of the light scattering is replaced by plausible rules of thumb that are much briefer than the real thing but give a realistic looking result – as long as no one looks too closely. There would be an economic and practical imperative for simulated realities to stay that way if they were purely for entertainment. But such limitations to the complexity of the simulation’s programming
would
presumably cause occasional tell-tale problems – and perhaps they would even be visible from within.
Even if the simulators were scrupulous about simulating the laws of Nature, there would be limits to what they could do. Assuming the simulators, or at least the early generations of them, have a very advanced knowledge of the laws of Nature, it’s likely they would still have incomplete knowledge of them (some philosophies of science would argue this must always be the case). They may know a lot about the physics and programming needed to simulate a universe, but there will be gaps or, worse still, errors in their knowledge of the laws of Nature. They would, of course, be subtle and far from obvious to us, otherwise our ‘advanced’ civilisation wouldn’t be advanced. These lacunae do not prevent simulations being created and running smoothly for long periods of time, but gradually the little flaws will begin to build up.
Eventually, their effects would snowball and these realities would cease to compute. The only escape is if their creators intervene to patch up the problems one by one as they arise. This is a solution that will be very familiar to the owner of any home computer who receives regular updates in order to protect it against new assaults by viruses or to repair gaps that its original creators had not foreseen. The creators of a simulation could offer this type of temporary protection, updating the working laws of Nature to include extra things they had learned since the simulation was initiated.
In this kind of situation, logical contradictions will inevitably arise and the laws in the simulations will appear to break down occasionally. The inhabitants of the simulation – especially the simulated scientists – will occasionally be puzzled by the observations they make. The simulated astronomers might, for instance, make observations that show that their so-called constants of Nature are very slowly changing.
It’s likely there could even be sudden glitches in the laws that govern these simulated realities. That’s because the simulators
would
most likely use a technique that has been found effective in all other simulations of complex systems: the use of error-correcting codes to put things back on track.
Take our genetic code, for example. If it were left to its own devices we would not last very long. Errors would accumulate and death and mutation would quickly ensue. We are protected from this by the existence of a mechanism for error correction that identifies and corrects mistakes in genetic coding. Many of our complex computer systems possess the same type of internal immune system to guard against error accumulation.
If the simulators used error-correcting computer codes to guard against the fallibility of their simulations as a whole (as well as simulating them on a smaller scale in our genetic code), then every so often a correction would take place to the state or the laws governing the simulation. Mysterious changes would occur that would appear to contravene the very laws of Nature that the simulated scientists were in the habit of observing and predicting.
So it seems enticing to conclude that, if we live in a simulated reality, we should expect to come across occasional ‘glitches’ or experimental results that we can’t repeat or even very slow drifts in the supposed constants and laws of Nature that we can’t explain.
