XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (736 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay
In parameters to function calls and in variables, squares on the board will always be represented by an integer in the range 0–63, which is calculated as
$row * 8 + $column
. When we use the square number to index the sequence that represents the board, we have to remember to add one.
The empty board is first initialized to a sequence of 64 zeroes, and the knight is then placed on its starting square by calling the function
place-knight
. Let's see how this function works.
Placing the Knight
This is a simple function:
for $i in 1 to 64 return
if ($i = $square + 1) then $move else $board[$i]” />
This function takes three parameters: the number of this move, the current state of the chessboard, and the square on which the knight is to be placed. When it's called from the root template, the move number is always one, and the board is always empty, but I will use the same function again later with different arguments.
What the function does is to copy the whole supplied chessboard before and after the square where the knight is to be placed. This square itself is replaced by the move number. For example, if the tour starts at square a8 (which translates to square zero), then the first call on
place-knight()
will return a sequence containing a one followed by 63 zeroes.
I can't, of course, modify the supplied chessboard in situ. All variables in XSLT are immutable. Instead I create a new board as a modified copy of the original. The result of the function is a sequence representing the new state of the chessboard after placing the knight.
There are various ways the actual calculation of the new board could have been written here. Another possibility would be:
$move,
$board[position() = $square+2 to 64]”/>
and a third option would be:
remove($board, $square+1),
$square+1,
$move) “/>
Displaying the Final Board
I'll skip the function that computes the knight's tour for the moment, and describe the relatively easy task of outputting the final result as HTML. Like the rest of the stylesheet, this logic is greatly simplified in XSLT 2.0:
Knight's tour starting at
select=“if ((($row + $column) mod 2)=1) then ‘xffff44’ else ‘white’”/>
The template contains a little bit of logic to achieve the traditional checkerboard coloring of the squares, using the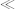
mod
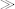operator to test whether the sum of the row number and the column number is a multiple of 2.
The actual content of each square is the move number, extracted from the relevant item in the sequence representing the board.
Finding the Route
So much for the input and output of the stylesheet, now for the substance: the algorithm to calculate the knight's tour.
The basic algorithm we use is that at each move, we consider all the squares we could go to, and choose the one with the fewest exits. For example, if we are on c2 then we could move to a1, e1, a3, e3, b4, or d4, assuming they are all unvisited. Of these, the corner square a1 has only one exit, namely b3, and if we don't visit the corner square now, then we'll never get another chance later. It turns out that this strategy of always visiting the square with least exits nearly always succeeds in generating a complete knight's tour, though in the rare cases where it doesn't, the algorithm is resilient enough to backtrack and try a different route if the first one fails.
The root template makes a call on the function named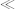make-moves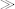. This function, starting from any given start position, works out all the moves needed to complete the knight's tour. Of course, it does this by recursion, but unlike previous functions which called themselves directly, this one does so indirectly, via another function namedtry-possible-moves.
The first thing themake-movesfunction does is to call the functionlist-possible-movesto construct a list of moves that are legal in the current situation. The result of this function, a list of moves, uses a very similar data structure to that of the chessboard itself. The list is represented as a sequence, and each possible move is represented by an integer whose value is the number of the square to which the knight travels. So in
Figure 20-3
, after move 5 the set of possible moves is the list (3, 19, 28, 30, 23). The list is in no particular order.
