XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (521 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay

Functions on QNames
local-name-from-QName()
826,
namespace-uri-from-QName()
841,
node-name()
843,
prefix-from-QName()
857,
QName()
858,
resolve-QName()
864.
Functions on Sequences
count()
733,
deep-equal()
745,
distinct-values()
749,
empty()
770,
exists()
778,
index-of()
807,
insert-before()
810,
remove()
861,
subsequence()
882,
unordered()
901.
Functions That Return Properties of Nodes
base-uri()
719,
data()
741,
document-uri()
764, †
generate-id()
797,
in-scope-prefixes()
808,
lang()
819,
local-name()
824,
name()
835,
namespace-uri()
837,
namespace-uri-for-prefix()
839,
nilled()
842,
node-name()
843,
root()
870,
string()
877, †
unparsed-entity-public-id()
902, †
unparsed-entity-uri()
902.
Functions That Find Nodes
collection()
726,
doc()
750, †
document()
754,
id()
802,
idref()
804, †
key()
812,
root()
870.
Functions That Return Context Information
base-uri()
719,
collection()
726, †
current()
734,
current-date()
738,
current-dateTime()
738, †
current-group()
739, †
current-grouping-key()
740,
current-time()
738,
default-collation()
748,
doc()
750,
implicit-timezone()
806,
last()
820,
position()
854, †
regex-group()
860.
Diagnostic Functions
error()
774,
trace()
896.
Functions That Return Information about the XSLT Environment
†
element-available()
764, †
function-available()
792, †
system-property()
890, †
type-available()
899
Functions That Assert a Static Type
exactly-one()
777,
one-or-more()
853,
zero-or-one()
912.
Notation
For each function (or for a closely related group of functions) there is an alphabetical entry in this chapter containing the following information:
- The name of the function
- A summary of the purpose of the function, often with a quick example
- Changes in 2.0
. In cases where a function was present in XSLT 1.0 or XPath 1.0, the entry for the function in this chapter contains a section that describes any changes in behavior introduced in the 2.0 version of the specs. If there are no changes, this section will say so. In cases where the function is new in XPath 2.0 or XSLT 2.0, this section is omitted. - The function signature, described below
- A section entitled
Effect
, which describes in fairly formal terms what the function does - Where appropriate, a section entitled
Usage
, which give advice on how to make best use of the function - A set of simple examples showing the function in action
- Cross-references to other related information in this book
Technically, a function in XPath is identified by its name and arity (number of arguments). This means that there is no formal relationship between the function
substring()
with two arguments and the function
substring()
with three arguments. However, the standard function library has been designed so that in cases like this where there are two functions with different arity, the functions in practice have a close relationship, and it is generally easier to think of them as representing one function with one or more of the arguments being optional. So this is how I have presented them.
The signatures of functions are defined with a table like the one that follows:
| Argument | Type | Meaning |
| input | xs:string? | The containing string |
| start | xs:double | The position in the containing string of … |
| length (optional) | xs:double | The number of characters to be included … |
| Result | xs:string | The required substring … |
The first column here gives a conventional name for the argument (or “Result” to label the row that describes the result of the function). Arguments to XPath functions are supplied by position, not by name, so the name given here is arbitrary; it is provided only to allow the argument to be referred to within the descriptive text. The text “(optional)” after the name of an argument indicates that this argument does not need to be supplied; in this case, this means that there is one version of the function with two arguments, and another version with three.
The second column gives the required type of the argument. The notation is that of the
SequenceType
syntax in XPath, introduced in Chapter 11. This consists of an item type followed optionally by an occurrence indicator (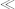 ?
?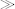 ,
,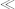 *
*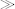 , or
, or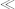 +
+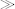 ). The item type is either the name of a built-in atomic type such as
). The item type is either the name of a built-in atomic type such as
xs:integer
or
xs:string
, or one of the following:
| Item type | Meaning |
| item() | Any item (either a node or an atomic value) |
| node() | Any node |
| element() | Any element node |
| xs:anyAtomicType | Any atomic value |
| Numeric | An xs:double , xs:float , xs:decimal , or xs:integer |
The occurrence indicator, if it is present, is either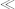 ?
?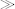 to indicate that the supplied argument can contain zero or one items of the specified item type, or
to indicate that the supplied argument can contain zero or one items of the specified item type, or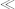 *
*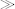 to indicate that it can be a sequence of zero or more items of the specified item type. (The occurrence indicator
to indicate that it can be a sequence of zero or more items of the specified item type. (The occurrence indicator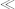 +
+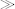 , meaning one or more, is not used in any of the standard functions.)
, meaning one or more, is not used in any of the standard functions.)
