XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (339 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay

The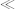 mod
mod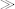 operator, which gives the remainder from an integer division, can be confusing when negative numbers are involved. I find the following rules of thumb helpful:
operator, which gives the remainder from an integer division, can be confusing when negative numbers are involved. I find the following rules of thumb helpful:
- The result is positive if the first operand is positive, negative if it is negative.
- The result depends only on the absolute value of the second operand, not on its sign.
It's also useful to think of the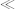 mod
mod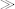 operator in conjunction with
operator in conjunction with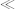 idiv
idiv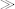 . Thus:
. Thus:

In all cases (except where
$y
is zero) the result of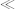 ($x idiv $y)*$y + ($x mod $y)
($x idiv $y)*$y + ($x mod $y)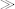 is
is
$x
.
Decimal Arithmetic
Decimal arithmetic is useful because it avoids the rounding errors that arise with floating-point calculations. This is particularly true when handling values that are discrete rather than continuous, of which the most obvious example is money.
Again, the language spec doesn't define the maximum precision that can be held in an
xs:decimal
value. This is more likely to be a problem with
xs:decimal
than with
xs:integer
, and it means that different products are likely to give different answers to the same calculation (though hopefully, only a little bit different!).
The main problem is with division. Even systems that support indefinite-precision
xs:decimal
values (as Saxon does, for example) have to make a decision as to how many digits to retain in the result of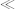 10 div 3
10 div 3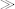 , and the spec offers no clues.
, and the spec offers no clues.
As with integer arithmetic, division by zero is a fatal error.
The rules for handling overflow are subtly different from the rules for integers. In the case of
xs:decimal
, overflow (that is, calculation of a result that is too big for the system to handle, whatever this limit might be) must be reported as an error. So unlike the situation with integers, there is no prospect of the system giving you a spurious result by wrapping around.
Arithmetic with
xs:decimal
values can also cause
underflow
. This happens when the result of a computation is smaller than the smallest value that can be recorded, but greater than zero. Equally, of course, it could be a very small negative number. For example, if you multiply
0.00000001
by itself, and the system can only handle 10 decimal places after the decimal point, you will get an underflow. The rule in this case is that the result returned must be the
xs:decimal
value
0.0
.
Floating-Point Arithmetic
Floating-point arithmetic (whether using single precision
xs:float
, or double-precision
xs:double
) is defined by the rules of the IEEE 754 specification. These rules were summarized in Chapter 5.
The XPath 1.0 specification tied the definition of floating-point arithmetic pretty closely to the same rules as were adopted in Java. But in fact, the IEEE 754 specification offers a number of options, and XPath 2.0 gives implementors a bit more freedom to select which options to provide. In particular, the specification allows for errors to be raised on overflow or underflow conditions, whereas the XPath 1.0 profile always returned positive or negative infinity in the overflow case, and positive or negative zero for underflow. So in corner cases, the behavior may not be exactly the same as with XPath 1.0, and not quite so consistent across different processors.
