World's 200 Hardest Brain Teasers (12 page)
Read World's 200 Hardest Brain Teasers Online
Authors: Dr. Gary R. Gruber

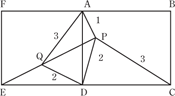
Note: MQA = 20° and
MQA = 20° and A =20°, so AM = MQ. But MQ = AP, since BC = AP and BC = MQ. Thus, AM = MQ, and so point M coincides with point P, making M = P. Now since triangle QRB is equilateral, QB = PQ, so
A =20°, so AM = MQ. But MQ = AP, since BC = AP and BC = MQ. Thus, AM = MQ, and so point M coincides with point P, making M = P. Now since triangle QRB is equilateral, QB = PQ, so QBP =
QBP = QPB = 10°. Since
QPB = 10°. Since B = 80°,
B = 80°, PBC = 70°.
PBC = 70°.
136. 135°
Rotate the points A, P, and D 90° counterclockwise about B to give the points E, Q, and F respectively. Clearly, PBQ = 90° and QA = PC = 3. By the Pythagorean theorem in triangle PBQ, PQ
PBQ = 90° and QA = PC = 3. By the Pythagorean theorem in triangle PBQ, PQ
2
= PB
2
+BQ
2
= 22 + 22 = 8 = QA
2
- AP
2
.
Hence, by the converse of the Pythagorean theorem in triangle PQA, we know that APQ = 90°. However, as triangle PBQ is right-angled and isosceles,
APQ = 90°. However, as triangle PBQ is right-angled and isosceles, BPQ = 45°.
BPQ = 45°.
Therefore, APB =
APB = APQ +
APQ + BPQ = 90° + 45° = 135°.
BPQ = 90° + 45° = 135°.
137. (c) flammable and (d) infamous
If we put the prefix
in
in front of each word, the meaning of the word means the opposite of the word, except for
flammable. (Inflammable
has the same meaning as
flammable)
and
famous (infamous
has the same meaning as
famous,
although
infamous
is
famous
in a bad way).
138. 30°
Draw BG at 20° to BC, cutting CA into CG and GA.
Then, GBD = 60° and
GBD = 60° and BGC and
BGC and BCG are 80°. So BC = BG.
BCG are 80°. So BC = BG.
