Warped Passages (60 page)

20

Warped Passage: A Solution to the Hierarchy Problem

What’s so small to you,

Is so large to me.

If it’s the last thing I do,

I’ll make you see.

Suzanne Vega

Athena awoke with a start. She had just revisited her recurring dream, which had again begun with her entering the dreamworld’s rabbit hole. In this episode, when the Rabbit announced, “Next stop, TwoDLand,” Athena ignored him and waited to hear the choices that remained.

At the three-spatial-dimensional stop, the Rabbit announced, “If you lived here, you’d be home by now.” But he refused to open the doors, despite Athena’s pleas that she did indeed live there and very much wanted to return home.

At the next stop, uniformed six-dimensioners tried to enter. But the Rabbit took one look at their inordinately large girth and abruptly closed the doors, saying that they couldn’t possibly fit. They quickly departed once the Rabbit threatened to cut them down to size.
^*

The elevator continued on its extraordinary journey. When it stopped again, the Rabbit announced “Warped Geometry—a five-dimensional world.”
^†
He gently pushed Athena towards the door, advising her, “Enter the funhouse mirror—it will take you home.” Since the Rabbit had mentioned a fifth dimension, Athena found this highly unlikely. But she didn’t have any choice but to enter and hope the tricky Rabbit was right.

When you learn a language, the words you remember depend on your particular needs or interests. On a bicycle trip in Italy, for example, I learned to ask for water in many different ways—
acqua di rubinetto
,
acqua minerale
,
acqua (minerale) gassata
,
acqua (minerale) naturale
, etc.
^*
Similarly, when learning about new physical scenarios, each physicist has her own perspective and her own questions, and might therefore notice certain aspects of a system or discover different implications of what is already known. Each of us can hear something different, even when faced with the same words or situation. It makes sense to listen carefully.

Raman and I had each been thinking about the hierarchy problem for years. But we were not searching for a new, better solution to the hierarchy problem when we began our collaboration. We were working on the model of sequestered supersymmetry breaking that I presented in Chapter 17. In the course of that work, we inadvertently discovered a remarkable
warped geometry
of spacetime (a particular type of curved geometry that we’ll soon explore) that was bounded by two branes. And because Raman and I were concerned with particle physics and the weakness of gravity, we immediately recognized the warped geometry’s potential significance: if the Standard Model of particle physics lies in this spacetime, the hierarchy problem could be solved. I’m not sure that we were the first to study this particular set of Einstein’s equations. But we were definitely the first to recognize this startling implication.

The next few chapters explain this and other remarkable possibilities of curved spacetime and how its consequences sometimes violate our expectations. This chapter focuses on a warped five-dimensional world that could help to explain the vast range of masses that are relevant to particle physics. Whereas in four-dimensional quantum field theory, particles are expected to have roughly the same masses,
in a warped higher-dimensional geometry this is no longer the case. Warped geometries provide a framework in which very disparate masses emerge naturally, and in which quantum effects are under control.

In the particular geometry described in this chapter, we’ll see that space is so strongly warped in the presence of two flat boundary branes that the hierarchy problem of particle physics is automatically solved—without the need for a large dimension, or for any arbitrary large number at all. In this scenario, one brane experiences a large gravitational force but the other does not. Spacetime changes so rapidly along the fifth dimension that it parlays a modest number associated with the separation between the two branes into a huge number (about ten million billion) associated with the relative strength of the gravitational force.

We’ll first explain the weakness of gravity on the second brane in terms of the graviton probability function, which determines the graviton’s interactions at any particular location in the fifth dimension. But we’ll also explain gravity’s weakness in different terms, based on the warped geometry itself rather than the graviton interaction strength. We’ll see that one of the amazing consequences of warped geometry is that size, mass, and even time depend on position along the fifth dimension. The warping of space and time in this two-brane setup is like the warping of time near the horizon of a black hole. But in this case, time dilates, geometry expands, and on one of the branes particles have a small mass—so the hierarchy problem gets automatically solved.

After discussing the warped geometry and its implications for the hierarchy problem, we’ll conclude this chapter with a discussion of the distinctive implications of the theory for future experiments. One of the most exciting aspects of this theory, as with the large extra-dimension models of the previous chapter, is that if it is correct it will very soon have observable consequences at particle accelerators. In fact, we’ll see they will be even more dramatic than the missing energy signature we discussed. The KK partners of the gravitons, though visitors from higher-dimensional space, will be distinguishable, visible particles that will decay into familiar particles on our four-dimensional brane.

Warped Geometry and Its Surprising Implications

The geometry that we’ll consider in this chapter contains two branes that bound a fifth dimension of space, as illustrated in Figure 78. This setup is similar to the one considered in Chapter 17 in that there are two branes with a fifth dimension that extends between them. However, it really is quite a different theory. The particles and the distribution of energy are different, and the theory is not supersymmetric. Nevertheless, as with that theory, we assume that all of the Standard Model particles, along with a Higgs particle responsible for breaking electroweak symmetry, are confined to one of the two branes.

Also as before, in this setup we’ll assume that gravity is the only force that exists throughout the fifth dimension. This means that were
it not for gravity, each of the branes would look like a conventional four-dimensional universe. Gauge bosons and particles confined to the branes would communicate forces and interact as if the fifth dimension didn’t exist. Standard Model particles would travel only in the three flat spatial brane dimensions, and forces would spread out only along the flat three-dimensional surface of the brane.
³⁵

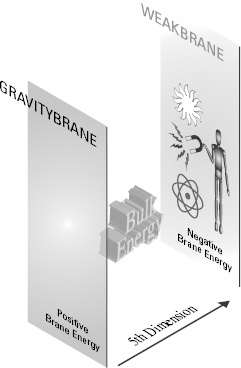
Figure 78.
The warped five-dimensional geometry with a single brane. The universe has five spacetime dimensions, but the Standard Model resides on a brane (the Weakbrane) that has four. Again, the total number of spacetime dimensions in this setup is five, whereas the number of spatial dimensions is four, three of which extend along the branes and one that extends between them.

Gravity, however, is different since it is not restricted to a brane, but instead exists in the full five-dimensional bulk. The force of gravity would be felt everywhere in the fifth dimension. But this does not necessarily mean that it is felt equally everywhere. Energy on the branes and in the five-dimensional bulk curves spacetime, and this makes an enormous difference to the gravitational field.

The large extra-dimensional theories of the previous chapter took advantage of the fact that branes could trap particles and forces, but neglected the energy that the branes themselves could carry. Raman and I weren’t sure that this was always a good assumption, since a central component of Einstein’s theory of general relativity is that energy induces a gravitational field, which means that when branes carry energy, they should curve space and time. In a universe with only a single extra dimension, which was what we intended to study, it was not at all clear that one could neglect brane and bulk energy: the gravitational effects of the brane don’t dissipate very rapidly, so one would expect distortions of spacetime, even far away from the branes.

We wanted to know how spacetime would curve in the presence of two energetic branes that bounded the extra dimension of space. Raman and I solved Einstein’s gravity equations for this two-brane setup, assuming that there was energy both in the bulk and on the branes. We discovered that such energy was indeed very important—the resulting spacetime was dramatically curved.

In some cases, curved spaces are easy to picture. The surface of a sphere, for example, is two-dimensional—you need only latitude and longitude to know your location—but it is nonetheless clearly curved. However, many curved spaces are more difficult to draw because they can’t readily be represented in three-dimensional space. The particular warped spacetime that we will now consider is such an example. It is part of a spacetime known as
anti de Sitter space
. Anti de Sitter space has negative curvature, more like a Pringles potato chip than a sphere.
The name comes from the Dutch mathematician and cosmologist Willem de Sitter, who studied a space with positive curvature that is now called
de Sitter space
. Although we don’t need the name here, we’ll refer to it later on when we connect this theory to a theory of anti de Sitter space that string theorists had been studying.

Although we’ll soon explore the interesting way in which the five-dimensional spacetime is curved, let’s first focus for a moment on the two branes at the edges of the fifth dimension. These two boundary branes are completely flat. If you were on the brane at either boundary, you would be stuck on a three-plus-one-dimensional world (three dimensions of space and one of time),
^*
which would extend infinitely far in the three spatial dimensions and look like flat spacetime, with no peculiar gravitational effects.

Furthermore, the curved spacetime has the special property that were you to restrict yourself to
any
single slice along the fifth dimension—not just the branes at the ends—you would find that this slice is completely flat. That is, although there aren’t branes anywhere in the fifth dimension except at the ends, the geometry of the three-plus-one-dimensional surfaces that you get by restricting yourself to any single five-dimensional point looks flat: it has the same shape as the large flat branes at the boundaries. If you think of the boundary branes as the heels of a loaf of bread, the flat, parallel four-dimensional regions at any location along the fifth dimension of spacetime are like the flat slices of bread from the interior of the loaf.

But the five-dimensional spacetime we are considering is nonetheless curved. That is reflected in the way the four-dimensional flat spacetime slices are glued together along the fifth dimension. I first spoke about this geometry at the Kavli Institute for Theoretical Physics in Santa Barbara, where the string theorist Tom Banks informed me that, technically speaking, the five-dimensional geometry Raman and I found is
warped
. Although many curved spacetimes are colloquially called warped, the technical term refers to geometries in which each slice is flat,
^†
but they are put together with an overall
warp factor
.
The warp factor is a function that changes the overall scale for position, time, mass, and energy at each point in the fifth dimension. This fascinating feature of warped geometry is subtle, and I’ll explain it further in the following section. The warp factor is also reflected in the graviton’s probability function and interactions that we’ll soon explore.

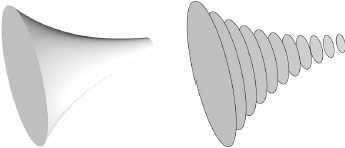
A curved space with flat slices is pictured in Figure 79. It is a filled-in funnel. We could slice the funnel into flat sheets with a cleaver, but the surface of the funnel is clearly curved. This is similar in some respects to the curved five-dimensional spacetime we’re considering. But the analogy isn’t perfect, because the boundary of the funnel, the funnel’s surface, is the only place where it’s curved, whereas in the warped spacetime the curvature is everywhere. This curvature would be reflected in an overall rescaling of the measuring rod of space and the clock speed for time, which would be different at each point in the fifth dimension.
³⁶