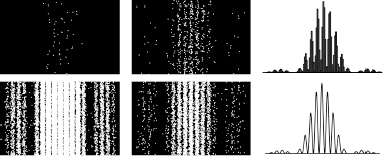
Warped Passages (22 page)

Figure 42.
Possible wave patterns for an electron according to the Bohr quantization.
Although Bohr’s proposal was radical and its meaning obscure, his guess did the trick: if true, it would guarantee stable electron orbits. Only particular electron orbits would be allowed. Intermediate orbits would be forbidden. In the absence of an external agent that could make an electron jump from one orbit to another, there would be no way for the electron to move in towards the nucleus.
You can think of Bohr’s atom with its fixed electron orbits as a multistory building in which you’re restricted to the even-numbered floors, the second, fourth, sixth, and so on. Since you could never set foot on the in-between floors, such as the third and the fifth, you would be eternally stuck on the even-numbered floor you were on. There would be no way to reach the ground floor and exit.
Bohr’s waves were an inspired assumption. He did not claim to know their meaning; he made his assumption simply to account for the stable electron orbits. Nevertheless, the quantitative nature of his proposal allowed it to be tested. In particular, Bohr’s hypothesis correctly predicted atomic spectral lines. Spectral lines give the frequency of light that an
un-ionized
atom—a neutral atom with all its electrons that carries zero net charge—emits or absorbs.
†
Physicists had noticed that spectra show a barcode-like pattern of stripes rather
than a continuous distribution (i.e., with all frequencies of light contributing). But no one understood why. Nor did they know the reason for the precise values of the frequencies they saw.
With his quantization hypothesis, Bohr could explain why photons were emitted or absorbed only at the measured frequencies. Although the electrons’ orbits were stable for an isolated atom, they could change when a photon with the right frequency—and hence, according to Planck, the right energy—delivered or removed energy.
Using classical reasoning, Bohr calculated the energy of the electrons that obeyed his quantization assumption. From these energies he predicted the energies, and hence the frequencies, of the photons that the hydrogen atom, which contains a single electron, emitted or absorbed. Bohr’s predictions were correct, and these correct predictions made his quantization assumption highly plausible. And this was what convinced Einstein, among others, that Bohr must be right.
The quantized packets of light, which could be emitted or absorbed and could thereby change electron orbits, can be compared to lengths of rope placed by the windows of the multistory building in our earlier analogy. If each piece of rope is precisely the length required to go from your floor to any of the other even-numbered floors, and only the windows to even-numbered floors are open, the rope would provide the means to change floors—but only between the even-numbered ones. In the same way, spectral lines could take only certain values, the values of the differences in energy between electrons that occupied permissible orbits.
Even though Bohr offered no explanation for his quantization condition, he certainly appeared to be correct. Many spectral lines had been measured, and his assumption could be used to reproduce them. If such agreement was a coincidence it would have been miraculous. Ultimately, quantum mechanics justified his assumption.
Particles’ Commitment Phobia
Important as the quantization proposals were, the quantum mechanical connection between particles and waves began to gel only with the advances made by the French physicist Prince Louis de Broglie,
the Austrian Erwin Schrödinger, and the German-born Max Born.
The first key step off the random walk of the old quantum theory onto the road of a real theory of quantum mechanics was de Broglie’s brilliant suggestion of turning Planck’s quantization hypothesis on its head. Whereas Planck had associated quanta with the waves of radiation, de Broglie—like Bohr—postulated that particles could also act like waves. De Broglie’s hypothesis meant that particles should exhibit wavelike properties and that those waves are determined by a particle’s momentum. (For low speeds, momentum is mass multiplied by speed. For all speeds, momentum tells how something responds to an applied force. Although at relativistic speeds, momentum is a more complicated function of mass and speed, the generalization of momentum that applies at high speeds also indicates how something at relativistic speeds would respond to a force.)
De Broglie assumed that a particle with momentum
p
was associated with a wave whose wavelength was inversely proportional to momentum—that is, the smaller the momentum, the longer the wavelength. The wavelength was also proportional to Planck’s constant,
h
.
*
The idea behind de Broglie’s proposal was that a wave that oscillated frenetically (that is, one with small wavelength) carried more momentum than one that oscillated lethargically (with large wavelength). Smaller wavelengths mean more rapid oscillations, which de Broglie associated with larger momentum.
If you find the existence of this particle-wave perplexing, that’s because it is. When de Broglie first suggested his waves, no one knew what they were supposed to be. Max Born proposed a surprising interpretation: that the wave was a function of position whose square gives the probability for finding a particle at any location in space.
†
He named this a
wavefunction
. Max Born’s insight was that particles cannot be pinned down and can be described only in terms of probabilities. This is a big a departure from classical assumptions. It means that you cannot know the particle’s exact location. You can only specify the
probability
of finding it somewhere.
But even though a quantum mechanical wave describes only probabilities, quantum mechanics predicts this wave’s precise evolution through time. Given the values at any one time, you can determine the values at any later time. Schrödinger developed the wave equation that shows the evolution of the wave associated with a quantum mechanical particle.
But what does this probability of finding a particle mean? It’s a puzzling idea—after all, there’s no such thing as a fraction of a particle. That a particle can be described by a wave was (and in some ways still is) one of the most surprising aspects of quantum mechanics, particularly as it is known that particles often behave like billiard balls, and not like waves. A particle interpretation and a wave interpretation seem incompatible.
The resolution to this apparent paradox hinges on the fact that you never detect the wave nature of a particle with just one particle. When you detect an individual electron, you see it in some definite location. In order to map out the entire wave, you need a set of identical electrons, or an experiment that is repeated many times. Even though each electron is associated with a wave, with a single electron you will measure only one number. But if you could prepare a large set of identical electrons, you would find that the fraction of electrons in each location is proportional to the probability wave assigned to an electron by quantum mechanics.
The wavefunction of an individual electron tells you about the likely behavior of many identical electrons with this same wavefunction. Any individual electron will be found only in a single place. But if there were many identical electrons, they would exhibit a wave-like distribution of locations. The wavefunction tells you the probability of the electron ending up in those locations.
This is analogous to the distribution of height in a population. Any individual has their own height, but the distribution tells us the likelihood that an individual will have any particular height. Similarly, even if one electron behaves like a particle, many electrons together will have a distribution of positions delineated by a wave. The distinction is that an individual electron is nonetheless associated with this wave.
In Figure 43 I’ve plotted an example of a probability function for
an electron. This wave gives the relative probability of finding the electron at a particular location. The curve I have drawn takes a definite value for every point in space (or rather, every point along a line, since the flatness of the paper forces me to draw only one dimension of space). If I could make many copies of this same electron, I could take a series of measurements of the electron’s position. I would find that the number of times I measured the electron to be at any particular point was proportional to this probability function. A bigger value means that the electron would be more likely to be found there; a smaller value that it is less likely. The wave reflects the cumulative effect of many electrons.
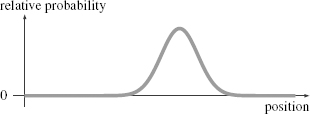
Figure 43.
An example of a probability function for an electron.
Even though you map out the wave with many electrons, what makes quantum mechanics special is that an individual electron is nonetheless described by a wave. That means you can never predict everything about that electron with certainty. If you measure its location, you will find it in a definite spot. But until you make that measurement, you can predict only that the electron has a particular probability of winding up there. You can’t say definitively where it will end up.
This particle-wave dichotomy is revealed in the famous double-slit experiment that Electra’s unknown origin in the opening story referred to.
11
Until 1961, when the German physicist Claus Jonsson actually performed it in the lab, the electron double-slit experiment was merely a thought experiment that physicists used to elucidate the meaning and consequences of the electron wavefunction. The experiment consists of an electron-emitter that sends electrons through a barrier pierced by two parallel slits (see Figure 44). The electrons pass through the slits and hit a screen behind the barrier, where they are recorded.
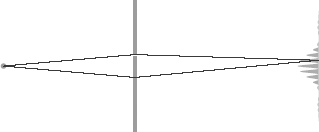
Figure 44.
Schematic arrangement of the double-slit electron interference experiment. Electrons can go through either of two slits before they hit a screen. The wave pattern that is recorded on the screen is a result of the interference of the two paths.
This experiment was meant to mimic a similar experiment that demonstrated the wavelike nature of light in the early nineteenth century. At that time, Thomas Young, a British physician, physicist, and Egyptologist,
*
sent monochromatic light through two slits and observed the wavelike pattern that light made on a screen behind the slits. The experiment demonstrated that light behaved like a wave. The point of imagining the same experiment with electrons is to see how you might observe the electron’s wavelike nature.
And indeed, if you were to perform the double-slit experiment with electrons, you would see what Young saw for light: a wavelike pattern on the screen behind the slits (see Figure 45). In the case of light, we understand that the wave is caused by interference. Some of the light goes through one slit and some of it goes though the other, and the wave pattern that is then recorded reflects the interference between the two. But what does a wavelike pattern mean for electrons?
The wavelike pattern on the screen tells us the very unintuitive fact that we should think of each electron as passing through both slits. You can’t know everything about an individual electron. Any electron can pass through either slit. Even though each electron’s location gets recorded when it reaches the screen, no one knows which of the two slits any individual electron passed through.
Quantum mechanics tells us that a particle can take any possible path from its starting point to its endpoint, and the wavefunction for
that particle reflects this fact. This is one of the many remarkable features of quantum mechanics. Unlike classical physics, quantum mechanics does not assign a particle a definite trajectory.