Understanding Computation (43 page)

If the input number is odd, the result is the stringo(for “odd”):
>>system=TagSystem.new('aabbbbbbbbbb',rulebook)=> #>>system.runaabbbbbbbbbb(the number 5)bbbbbbbbbbccbbbbbbbbccdbbbbbbccddbbbbccdddbbccddddccddddddddddeodddeodeoo=> nil

The number is halved as before, but because it’s an odd number this time, the result
is a string with an odd number ofds. Our encoding
scheme for numbers uses only pairs of characters, soccddddddoesn’t strictly represent anything, but because it contains “two and
a half” pairs ofdcharacters, it’s reasonable to think
of it informally as the number 2.5.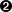
All the leading
ddpairs get
deleted, leaving a solitarydbefore the finaleo.
The leftover
dis deleted and
takes theewith it, leaving justo, and the system halts.
Having a deletion number greater than 1 is essential for making this tag system work.
Because every
second
character triggers a rule, we can influence the
system’s behavior by arranging for certain characters to appear (or not appear) in these
trigger positions. This technique of making characters appear in or out of sync with the
deletion behavior is the key to designing a powerful tag system.
These number-manipulating techniques can be used to simulate a
Turing machine. Building a Turing machine simulation on top of something
as simple as a tag system involves a lot of detail, but one way of doing
it works (very roughly) like this:
As the simplest possible example, take a Turing machine whose
tape only uses two characters—we’ll call them0and1,
with0acting as the blank
character.Split the Turing machine’s tape into two pieces: the left part,
consisting of the character underneath the tape head itself and all
characters to its left, and the right part, consisting of all
characters to the right of the head.Treat the left part of the tape as a binary number: if the
initial tape looks like0001101(0)0011000, the left part is the
binary number 11010, which is 26 in decimal.Treat the right part of the tape as a binary number
written
backward
: the right part of our example tape is the binary number 1100, or 12
in decimal.Encode those two numbers as a string suitable for use by a tag system. For our example
tape, we could useaafollowed by 26 copies ofbb, thenccfollowed by 12
copies ofdd.Use simple numerical operations—doubling, halving, incrementing,
decrementing, and odd/even checking—to simulate reading from the tape,
writing to the tape, and moving the tape head. For instance, we can
move the head right on our example tape by doubling the number
representing the left part and halving the number representing the
right part:
[
59
]
doubling 26 gives 52, which is 110100 in binary; half of
12 is 6, which is 110 in binary; so the new tape looks like011010(0)011000. Reading from the tape means
checking whether the number representing the left part of the tape is
even or odd, and writing a1or0to the tape means incrementing or
decrementing that number.Represent the current state of the simulated Turing machine with the choice of
characters used to encode the left and right tape numbers: perhaps when the machine is in
state 1, we encode the tape witha,b,c, anddcharacters, but when it moves into state 2, we usee,f,g, andhinstead, and so
on.Turn each Turing machine rule into a tag system that rewrites
the current string in the appropriate way. A rule that reads a0, writes a1, moves the tape head right and goes into
state 2 could become a tag system that checks that the left tape
number is even, increments it, doubles the left tape number while
halving the right tape number, and produces a final string that is
encoded with state 2’s characters.Combine these individual tag systems to make one large system
that simulates every rule of the
Turing machine.

