Thinking, Fast and Slow (35 page)
Read Thinking, Fast and Slow Online
Authors: Daniel Kahneman

As Allais had anticipated, the sophisticated participants at the meeting did not notice that their preferences violated utility theory until he drew their attention to that fact as the meeting was about to end. Allais had intended this announcement to be a bombshell: the leading decision theorists in the world had preferences that were inconsistent with their own view of rationality! He apparently believed that his audience would be persuaded to give up the approach that Bima ahat Bimhe rather contemptuously labeled “the American school” and adopt an alternative logic of choice that he had developed. He was to be sorely disappointed.
Economists who were not aficionados of decision theory mostly ignored the Allais problem. As often happens when a theory that has been widely adopted and found useful is challenged, they noted the problem as an anomaly and continued using expected utility theory as if nothing had happened. In contrast, decision theorists—a mixed collection of statisticians, economists, philosophers, and psychologists—took Allais’s challenge very seriously. When Amos and I began our work, one of our initial goals was to develop a satisfactory psychological account of Allais’s paradox.
Most decision theorists, notably including Allais, maintained their belief in human rationality and tried to bend the rules of rational choice to make the Allais pattern permissible. Over the years there have been multiple attempts to find a plausible justification for the certainty effect, none very convincing. Amos had little patience for these efforts; he called the theorists who tried to rationalize violations of utility theory “lawyers for the misguided.” We went in another direction. We retained utility theory as a logic of rational choice but abandoned the idea that people are perfectly rational choosers. We took on the task of developing a psychological theory that would describe the choices people make, regardless of whether they are rational. In prospect theory, decision weights would not be identical to probabilities.
Decision Weights
Many years after we published prospect theory, Amos and I carried out a study in which we measured the decision weights that explained people’s preferences for gambles with modest monetary stakes. The estimates for gains are shown in table 4.

Table 4
You can see that the decision weights are identical to the corresponding probabilities at the extremes: both equal to 0 when the outcome is impossible, and both equal to 100 when the outcome is a sure thing. However, decision weights depart sharply from probabilities near these points. At the low end, we find the possibility effect: unlikely events are considerably overweighted. For example, the decision weight that corresponds to a 2% chance is 8.1. If people conformed to the axioms of rational choice, the decision weight would be 2—so the rare event is overweighted by a factor of 4. The certainty effect at the other end of the probability scale is even more striking. A 2% risk of
not
winning the prize reduces the utility of the gamble by 13%, from 100 to 87.1.
To appreciate the asymmetry between the possibility effect and the certainty effect, imagine first that you have a 1% chance to win $1 million. You will know the outcome tomorrow. Now, imagine that you are almost certain to win $1 million, but there is a 1% chance that you will not. Again, you will learn the outcome tomorrow. The anxiety of the second situation appears to be more salient than the hope in the first. The certainty effect is also more striking than the possibility effect if the outcome is a surgical disaster rather than a financial gain. Compare the intensity with which you focus on the faint sliver of hope in an operation that is almost certain to be fatal, compared to the fear of a 1% risk.
< Bimp height="0%" width="5%">The combination of the certainty effect and possibility effects at the two ends of the probability scale is inevitably accompanied by inadequate sensitivity to intermediate probabilities. You can see that the range of probabilities between 5% and 95% is associated with a much smaller range of decision weights (from 13.2 to 79.3), about two-thirds as much as rationally expected. Neuroscientists have confirmed these observations, finding regions of the brain that respond to changes in the probability of winning a prize. The brain’s response to variations of probabilities is strikingly similar to the decision weights estimated from choices.
Probabilities that are extremely low or high (below 1% or above 99%) are a special case. It is difficult to assign a unique decision weight to very rare events, because they are sometimes ignored altogether, effectively assigned a decision weight of zero. On the other hand, when you do not ignore the very rare events, you will certainly overweight them. Most of us spend very little time worrying about nuclear meltdowns or fantasizing about large inheritances from unknown relatives. However, when an unlikely event becomes the focus of attention, we will assign it much more weight than its probability deserves. Furthermore, people are almost completely insensitive to variations of risk among small probabilities. A cancer risk of 0.001% is not easily distinguished from a risk of 0.00001%, although the former would translate to 3,000 cancers for the population of the United States, and the latter to 30.
When you pay attention to a threat, you worry—and the decision weights reflect how much you worry. Because of the possibility effect, the worry is not proportional to the probability of the threat. Reducing or mitigati
ng the risk is not adequate; to eliminate the worry the probability must be brought down to zero.
The question below is adapted from a study of the rationality of consumer valuations of health risks, which was published by a team of economists in the 1980s. The survey was addressed to parents of small children.
Suppose that you currently use an insect spray that costs you $10 per bottle and it results in 15 inhalation poisonings and 15 child poisonings for every 10,000 bottles of insect spray that are used.
You learn of a more expensive insecticide that reduces each of the risks to 5 for every 10,000 bottles. How much would you be willing to pay for it?
The parents were willing to pay an additional $2.38, on average, to reduce the risks by two-thirds from 15 per 10,000 bottles to 5. They were willing to pay $8.09, more than three times as much, to eliminate it completely. Other questions showed that the parents treated the two risks (inhalation and child poisoning) as separate worries and were willing to pay a certainty premium for the complete elimination of either one. This premium is compatible with the psychology of worry but not with the rational model.
The Fourfold Pattern
When Amos and I began our work on prospect theory, we quickly reached two conclusions: people attach values to gains and losses rather than to wealth, and the decision weights that they assign to outcomes are different from probabilities. Neither idea was completely new, but in combination they explained a distinctive pattern of preferences that we ca Bima ae ca Bimlled the fourfold pattern. The name has stuck. The scenarios are illustrated below.
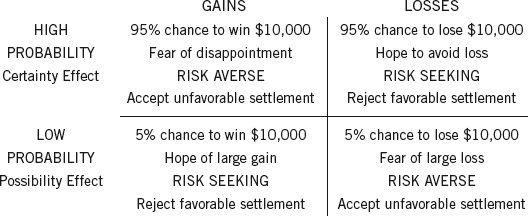
Figure 13
- The top row in each cell shows an illustrative prospect.
- The second row characterizes the focal emotion that the prospect evokes.
- The third row indicates how most people behave when offered a choice between a gamble and a sure gain (or loss) that corresponds to its expected value (for example, between “95% chance to win $10,000” and “$9,500 with certainty”). Choices are said to be risk averse if the sure thing is preferred, risk seeking if the gamble is preferred.
- The fourth row describes the expected attitudes of a defendant and a plaintiff as they discuss a settlement of a civil suit.
The
fourfold pattern
of preferences is considered one of the core achievements of prospect theory. Three of the four cells are familiar; the fourth (top right) was new and unexpected.
- The top left is the one that Bernoulli discussed: people are averse to risk when they consider prospects with a substantial chance to achieve a large gain. They are willing to accept less than the expected value of a gamble to lock in a sure gain.
- The possibility effect in the bottom left cell explains why lotteries are popular. When the top prize is very large, ticket buyers appear indifferent to the fact that their chance of winning is minuscule. A lottery ticket is the ultimate example of the possibility effect. Without a ticket you cannot win, with a ticket you have a chance, and whether the chance is tiny or merely small matters little. Of course, what people acquire with a ticket is more than a chance to win; it is the right to dream pleasantly of winning.
- The bottom right cell is where insurance is bought. People are willing to pay much more for insurance than expected value—which is how insurance companies cover their costs and make their profits. Here again, people buy more than protection against an unlikely disaster; they eliminate a worry and purchase peace of mind.
The results for the top right cell initially surprised us. We were accustomed to think in terms of risk aversion except for the bottom left cell, where lotteries are preferred. When we looked at our choices for bad options, we quickly realized that we were just as risk seeking in the domain of losses as we were risk averse in the domain of gains. We were not the first to observe risk seeking with negative prospects—at least two authors had reported that fact, but they had not made much of it. However, we were fortunate to have a framework that made the finding of risk seeking easy to interpret, and that was a milestone in our thinking. Indeed, we identified two reasons for this effect.
First, there is diminishing sensitivity. The sure loss is very aversive because the reaction to a loss of $900 is more than 90% as intense as the reaction to a loss of $1,000. The second factor may be even more powerful: the decision weight that corresponds to a probability of 90% is only about 71, much lower than the probability. The result is that when you consider a choice between a sure loss and a gamble with a high probability o Bima aty o Bimf a larger loss, diminishing sensitivity makes the sure loss more aversive, and the certainty effect reduces the aversiveness of the gamble. The same two factors enhance the attractiveness of the sure thing and reduce the attractiveness of the gamble when the outcomes are positive.
The shape of the value function and the decision weights both contribute to the pattern observed in the top row of table 13. In the bottom row, however, the two factors operate in opposite directions: diminishing sensitivity continues to favor risk aversion for gains and risk seeking for losses, but the overweighting of low probabilities overcomes this effect and produces the observed pattern of gambling for gains and caution for losses.
Many unfortunate human situations unfold in the top right cell. This is where people who face very bad options take desperate gambles, accepting a high probability of making things worse in exchange for a small hope of avoiding a large loss. Risk taking of this kind often turns manageable failures into disasters. The thought of accepting the large sure loss is too painful, and the hope of complete relief too enticing, to make the sensible decision that it is time to cut one’s losses. This is where businesses that are losing ground to a superior technology waste their remaining assets in futile attempts to catch up. Because defeat is so difficult to accept, the losing side in wars often fights long past the point at which the victory of the other side is certain, and only a matter of time.
Gambling in the Shadow of the Law
The legal scholar Chris Guthrie has offered a compelling application of the fourfold pattern to two situations in which the plaintiff and the defendant in a civil suit consider a possible settlement. The situations differ in the strength of the plaintiff’s case.
