The Panda’s Thumb (29 page)
Authors: Stephen Jay Gould

J. P. M
ORGAN, MEETING
with Henry Ford in E. L. Doctorow's
Ragtime
, praises the assembly line as a faithful translation of nature's wisdom:
Has it occurred to you that your assembly line is not merely a stroke of industrial genius but a projection of organic truth? After all, the interchangeability of parts is a rule of natureâ¦. All mammals reproduce in the same way and share the same designs of self-nourishment, with digestive and circulatory systems that are recognizably the same, and they enjoy the same sensesâ¦. Shared design is what allows taxonomists to classify mammals as mammals.
An imperious tycoon should not be met with equivocation; nonetheless, I can only reply “yes, and no” to Morgan's pronouncement. Morgan was wrong if he thought that large mammals are geometric replicas of smaller relatives. Elephants have relatively smaller brains and thicker legs than mice, and these differences record a general rule of mammalian design, not the idiosyncracies of particular animals.
But Morgan was right in arguing that large animals are essentially similar to small members of their group. The similarity, however, does not reside in a constant shape. The basic laws of geometry dictate that animals must change their shape in order to work the same way at different sizes. Galileo himself established the classic example in 1638: the strength of an animal's leg is a function of its cross-sectional area (length à length); the weight that legs must support varies as the animal's volume (length à length à length). If mammals did not increase the relative thickness of their legs as they got larger, they would soon collapse (since body weight would increase so much faster than the supporting strength of limbs). To remain the same in function, animals must change their form.
The study of these changes in form is called “scaling theory.” Scaling theory has uncovered a striking regularity of changing shape over the 25-millionfold range of mammalian weight from shrew to blue whale. If we plot brain weight versus body weight for all mammals on the so-called mouse-to-elephant (or shrew-to-whale) curve, very few species deviate far from a single line expressing the general rule: brain weight increases only two-thirds as fast as body weight as we move from small to large mammals. (We share with bottle-nosed dolphins the honor of greatest upward deviance from the curve.)
We can often predict these regularities from the basic physics of objects. The heart, for example, is a pump. Since all mammalian hearts work in essentially the same way, small hearts must pump considerably faster than large ones (imagine how much faster you could work a finger-sized, toy bellows than the giant model that fuels a blacksmith's forge or an old-fashioned organ). On the mouse-to-elephant curve for mammals, the length of a heartbeat increases between one-fourth and one-third as fast as body weight as we move from small to large mammals. The generality of this conclusion has recently been affirmed in an interesting study by J. E. Carrel and R. D. Heathcote on the scaling of heart rate in spiders. They used a cool laser beam to illuminate the hearts of resting spiders and drew a crab spider-to-tarantula curve for eighteen species spanning nearly a thousandfold range of body weight. Again, scaling is regular with heart rate, increasing four-tenths as fast as body weight (.409 times as fast, to be exact).
We may extend this conclusion for hearts to a general statement about the pace of life in small versus large animals. Small animals tick through life far more rapidly than large animalsâtheir hearts work more quickly, they breathe more frequently, their pulse beats much faster. Most importantly, metabolic rate, the so-called fire of life, increases only three-fourths as fast as body weight in mammals. To keep themselves going, large mammals do not need to generate as much heat per unit of body weight as small animals. Tiny shrews move frenetically, eating nearly all their waking lives to keep their metabolic fire burning at the maximal rate among mammals; blue whales glide majestically, their hearts beating the slowest rhythm among active, warmblooded creatures.
The scaling of lifetime among mammals suggests an intriguing synthesis of these disparate data. We have all had enough experience with mammalian pets of various sizes to understand that small mammals tend to live for a shorter time than large ones. In fact, mammalian lifetime scales at about the same rate as heartbeat and breath timeâbetween one-fourth and one-third as fast as body weight as we move from small to large animals. (
Homo sapiens
emerges from this analysis as a very peculiar animal. We live far longer than a mammal of our body size should. In essay 9, I argue that humans evolved by an evolutionary process called “neoteny”âthe preservation in adults of shapes and growth rates that characterize juvenile stages of ancestral primates. I also believe that neoteny is responsible for our elevated longevity. Compared with other mammals, all stages of human life arrive “too late.” We are born as helpless embryos after a long gestation; we mature late after an extended childhood; we die, if fortune be kind, at ages otherwise reached by warmblooded animals only at the very largest sizes.)
Usually, we pity the pet mouse or gerbil that lived its full span of a year or two at most. How brief its life, while we endure for the better part of a century. As the main theme of this essay, I want to argue that such pity is misplaced (our personal grief, of course, is quite another matter; with this, science does not deal). Morgan was right in
Ragtimeâ
small and large mammals are essentially similar. Their lifetimes are scaled to their life's pace, and all endure for approximately the same amount of biological time. Small mammals tick fast, burn rapidly, and live for a short time; large mammals live long at a stately pace. Measured by their own internal clocks, mammals of different sizes tend to live for the same amount of time.
We are prevented from grasping this important and comforting concept by a deeply ingrained habit of Western thought. We are trained from earliest memory to regard absolute Newtonian time as the single valid measuring stick in a rational and objective world. We impose our kitchen clock, ticking equably, upon all things. We marvel at the quickness of a mouse, express boredom at the torpor of a hippopotamus. Yet each is living at the appropriate pace of its own biological clock.
I do not wish to deny the importance of absolute, astronomical time to organisms (see essay 31). Animals must measure it to lead successful lives. Deer must know when to regrow their antlers, birds when to migrate. Animals track the day-night cycle with their circadian rhythms; jet lag is the price we pay for moving much faster than nature intended.
But absolute time is not the appropriate measuring stick for all biological phenomena. Consider the magnificent song of the humpback whale. E. O. Wilson has described the awesome effect of these vocalizations: “The notes are eerie yet beautiful to the human ear. Deep basso groans and almost inaudibly high soprano squeaks alternate with repetitive squeals that suddenly rise or fall in pitch.” We do not know the function of these songs. Perhaps they enable whales to find each other and to stay together during their annual transoceanic migrations. Perhaps they are the mating songs of courting males.
Each whale has its own characteristic song; the highly complex patterns are repeated over and over again with great faithfulness. No scientific fact that I have learned in the last decade struck me with more force than Roger S. Payne's report that the length of some songs may extend for more than half an hour. I have never been able to memorize the five-minute first
Kyrie
of the B-minor Mass (and not for want of trying); how could a whale sing for thirty minutes and then repeat itself accurately? Of what possible use is a thirty-minute repeat cycleâfar too long for a human to recognize; we would never grasp it as a single song (without Payne's recording machinery and much study after the fact). But then I remembered the whale's metabolic rate, the enormously slow pace of its life compared with ours. What do we know about a whale's perception of thirty minutes? A humpback may scale the world to its own metabolic rate; its half-hour song may be our minute waltz. From any point of view, the song is spectacular; it is the most elaborate single display so far discovered in any animal. I merely urge the whale's point of view as an appropriate perspective.
We can provide some numerical precision to support the claim that all mammals, on average, live for the same amount of biological time. In a method developed by W. R. Stahl, B. Günther, and E. Guerra in the late 1950s and early 1960s, we search the mouse-to-elephant equations for biological properties that scale at the same rate against body weight. For example, Günther and Guerra give the following equations for mammalian breath time and heartbeat time versus body weight.
Â
breath time = .0000470 body
0.28
heartbeat time = .0000119 body
0.28
Â
(Nonmathematical readers need not be overwhelmed by the formalism. The equations simply state that both breath time and heartbeat time increase about .28 times as fast as body weight as we move from small to large mammals.) If we divide the two equations, body weight cancels out because it is raised to the same power in both.
Â
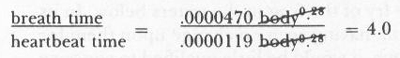
Â
This states that the ratio of breath time to heartbeat time is 4.0 in mammals of any body size. In other words, all mammals, whatever their size, breathe once for each four heartbeats. Small mammals breathe and beat their hearts faster than large mammals, but both breath and heart slow up at the same relative rate as mammals get larger.
Lifetime also scales at the same rate as body weight (.28 times as fast as we move from small to large mammals). This means that the ratio of both breath time and heartbeat time to lifetime is also constant over the entire range of mammalian size. When we perform a calculation similar to the one above, we find that all mammals, regardless of their size, tend to breathe about 200 million times during their lives (their hearts, therefore, beat about 800 million times). Small mammals breathe fast, but live for a short time. Measured by the internal clocks of their own hearts or the rhythm of their own breathing, all mammals live the same time. (Astute readers, after counting their breaths or taking their pulses, may have calculated that they should have died long ago. But
Homo sapiens
is a markedly deviant mammal in more ways than braininess alone. We live about three times as long as mammals of our body size “should,” but we breathe at the “right” rate and thus live to breathe about three times as often as an average mammal of our body size. I regard this excess of living as a happy consequence of neoteny.)
The mayfly lives but a day as an adult. It may, for all I know, experience that day as we live a lifetime. Yet all is not relative in our world, and such a short glimpse of it guarantees distortion in interpreting events ticking on longer scales. In a brilliant metaphor, the pre-Darwinian evolutionist Robert Chambers wrote in 1844 of a mayfly watching the metamorphosis of a tadpole into a frog:
Suppose that an ephemeron [a mayfly], hovering over a pool for its one April day of life, were capable of observing the fry of the frog in the waters below. In its aged afternoon, having seen no change upon them for such a long time, it would be little qualified to conceive that the external branchiae [gills] of these creatures were to decay, and be replaced by internal lungs, that feet were to be developed, the tail erased, and the animal then to become a denizen of the land.
Human consciousness arose but a minute before midnight on the geologic clock. Yet we mayflies try to bend an ancient world to our purposes, ignorant perhaps of the messages buried in its long history. Let us hope that we are still in the early morning of our April day.
THE FAMOUS WORDS
“blessed art thou among women” were uttered by the angel Gabriel as he announced to Mary that she would conceive by the Holy Spirit. In medieval and Renaissance painting, Gabriel bears the wings of a bird, often elaborately spread and adorned. While visiting Florence last year, I became fascinated by the “comparative anatomy” of Gabriel's wings as depicted by the great painters of Italy. The faces of Mary and Gabriel are so beautiful, their gestures often so expressive. Yet the wings, as painted by Fra Angelico or by Martini, seem stiff and lifeless, despite the beauty of their intricate feathering.
But then I saw Leonardo's version. Gabriel's wings are so supple and graceful that I scarcely cared to study his face or note the impact he had upon Mary. And then I recognized the source of the difference. Leonardo, who studied birds and understood the aerodynamics of wings, had painted a working machine on Gabriel's back. His wings are both beautiful and efficient. They have not only the right orientation and camber, but the correct arrangement of feathers as well. Had he been just a bit lighter, Gabriel might have flown without divine guidance. In contrast, the other Gabriels bear flimsy and awkward ornaments that could never work. I was reminded that aesthetic and functional beauty often go hand in hand (or rather arm in arm in this case).
In the standard examples of nature's beautyâthe cheetah running, the gazelle escaping, the eagle soaring, the tuna coursing, and even the snake slithering or the inchworm inchingâwhat we perceive as graceful form also represents an excellent solution to a problem in physics. When we wish to illustrate the concept of adaptation in evolutionary biology, we often try to show that organisms unconsciously “know” physicsâthat they have evolved remarkably efficient machines for eating and moving. When Mary asked Gabriel how she could possibly conceive, “seeing I know not a man,” the angel replied: “For with God nothing shall be impossible.” Many things are impossible for nature. But what nature can do, she often does surpassingly well. Good design is usually expressed by correspondence between an organism's form and an engineer's blueprint.
I recently encountered an even more striking example of good design: an organism that builds an exquisite machine directly within its own body. The machine is a magnet; the organism, a “lowly” bacterium. When Gabriel departed, Mary went to visit Elizabeth, who had also conceived with a bit of help from on high. Elizabeth's babe (the future John the Baptist) “leaped in her womb” and Mary pronounced the
Magnificat
, including the line (later set so incomparably by Bach)
et exaltavit humilisâ
“and he hath exalted them of low degree.” The tiny bacteria, simplest in structure among organisms, inhabitants of the first rung on traditional (and fallacious) ladders of life, illustrate in a few microns all the wonder and beauty that some organisms require meters to express.
In 1975, University of New Hampshire microbiologist Richard P. Blakemore discovered “magnetotactic” bacteria in sediments near Woods Hole, Massachusetts. (Just as geotactic organisms orient toward gravitational fields and phototactic creatures toward light, magnetotactic bacteria align themselves and swim in preferred directions within magnetic fields.) Blakemore then spent a year at the University of Illinois with microbiologist Ralph Wolfe and managed to isolate and culture a pure strain of magnetotactic bacteria. Blakemore and Wolfe then turned to an expert on the physics of magnetism, Richard B. Frankel of the National Magnet Laboratory at M.I.T. (I thank Dr. Frankel for his patient and lucid explanation of their work.)
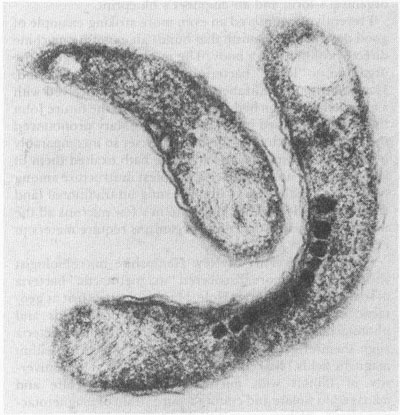
A magnetotactic bacterium with its chain of tiny magnets (X 40,000)
D. L. BALKWILL AND D. MARATEA
Frankel and his colleagues found that each bacterium builds within its body a magnet made of twenty or so opaque, roughly cubic particles, measuring about 500 angstroms on a side (an angstrom is one ten-millionth of a millimeter). These particles are made primarily of the magnetic material Fe
3
0
4
, called magnetite, or lodestone. Frankel then calculated the total magnetic moment per bacterium and found that each contained enough magnetite to orient itself in the earth's magnetic field against the disturbing influence of Brownian motion. (Particles small enough to be unaffected by the gravitational fields that stabilize us or by the surface forces that affect objects of intermediate size are buffeted in a random manner by thermal energy of the medium in which they lie suspended. The “play” of dust particles in sunlight provides a standard illustration of Brownian motion.)
The magnetotactic bacteria have built a remarkable machine, using virtually the only configuration that could work as a compass within their tiny bodies. Frankel explains why the magnetite must be arranged as particles and why the particles must be about 500 angstroms on a side. To work as an efficient compass, magnetite must be present as so-called single domain particles, that is, as bits with a single magnetic moment, containing opposite north- and south-seeking ends. The bacteria contain a chain of such particles, oriented with their magnetic moments north pole to the next south pole along the rowâ“like the elephants head to tail in a circus finale,” as Frankel states. In this way, the entire chain of particles operates as a single magnetic dipole with north- and south-seeking ends.
If the particles were a bit smaller (less than 400 angstroms on a side), they would be “superparamagnetic”âa big word indicating that thermal energy at room temperature would cause internal reorientation of the particle's magnetic moment. On the other hand, if particles were greater than 1,000 angstroms on a side, separate magnetic domains pointing in different directions would form
within
the particle. This “competition” would reduce or cancel the particle's overall magnetic moment. Thus, Frankel concludes, “the bacteria have solved an interesting problem in physics by producing particles of magnetite of just the right size for a compass, of dimension 500 angstroms.”
But evolutionary biology is preeminently the science of “why,” and we must ask what such a small creature could possibly do with a magnet. Since a bacterium's cruising range is probably a few inches for the few minutes of its existence, I find it hard to believe that oriented motion in a north or south direction can play any role in its repertoire of adaptive traits. But what preferred direction of motion might make a difference? Frankel suggests, quite plausibly in my view, that an ability to move
down
might be crucial for such a bacteriumâfor down is the direction of sediments in aquatic environments, and down might lead to a region of preferred oxygen pressure. In this instance, “them of low degree” might wish to debase themselves even further.
But how does a bacterium know which way is down? With the smug prejudices of our enormous selves, we might think the question inane for its obvious answer: all they have to do is stop whatever they are doing and fall. Not at all. We fall because gravity affects us. Gravityâthe standard example of a “weak force” in physicsâinfluences us only because we are large. We live in a world of competing forces, and the relative strength of these forces depends primarily upon the size of objects affected by them. For familiar creatures of macroscopic dimensions, the ratio of surface area to volume is crucial. This ratio decreases continually as an organism grows, since areas increase as length squared and volumes as length cubed. Small creatures, insects for example, live in a world dominated by forces acting on their surfaces. Some can walk on water or hang upside down from a ceiling because surface tension is so strong and the gravitational force that might pull them down so weak. Gravitation works on volumes (or, to be more precise, upon masses that are proportional to volumes in a constant gravitational field). Gravitation rules us with our low ratio of surface to volume. But it troubles an insect very littleâand a bacterium not at all.
The world of a bacterium is so unlike our own that we must abandon all our certainties about the way things are and start from scratch. Next time you see
Fantastic Voyage
on the tube, take your eyes off Raquel Welch and the predaceous white blood corpuscle long enough to ponder how the miniaturized adventurers would really fare as microscopic objects within a human body (they behave just like regular folks in the film). They would, first of all, be subject to shocks of the Brownian motion, thus making the film something of a random blur. Also, as Isaac Asimov pointed out to me, their ship could not run on its propeller, since blood is too viscous at such a scale. It should have, he said, a flagellumâlike a bacterium.
D'Arcy Thompson, premier student of scaling since Galileo, urged us to set aside our prejudices if we would understand the world of a bacterium. In his masterpiece,
Growth and Form
(published in 1942 but still in print), he ends his chapter “On Magnitude” in his incomparable prose:
Life has a range of magnitude narrow indeed compared to that with which physical science deals; but it is wide enough to include three such discrepant conditions as those in which a man, an insect and a bacillus have their being and play their several roles. Man is ruled by gravitation, and rests on mother earth. A water-beetle finds the surface of a pool a matter of life and death, a perilous entanglement or an indispensable support. In a third world, where the bacillus lives, gravitation is forgotten, and the viscosity of the liquid, the resistance defined by Stokes's law, the molecular shocks of the Brownian movement, doubtless also the electric charges of the ionized medium, make up the physical environment and have their potent and immediate influence upon the organism. The predominant factors are no longer those of our scale; we have come to the edge of a world of which we have no experience, and where all our preconceptions must be recast.
So how does a bacterium know which way is down? We use magnets for horizontal orientation so exclusively that we often forget (in fact, I suspect many of us do not know) that the earth's magnetic field also has a vertical component, its strength depending upon latitude. (We damp out the vertical deflection in building compasses because it doesn't interest us. As large creatures ruled by gravitation, we know which way is down. Only at our scale could folly be personified as not knowing “which way is up.”) A compass needle follows the earth's lines of force. At the equator, these lines are horizontal to the surface. Toward the poles, they dip more and more strongly
into
the earth. At the magnetic pole itself, the needle points straight down. At my latitude in Boston, the vertical component is actually stronger than the horizontal. A bacterium, swimming north as a free compass needle, also swims down at Woods Hole.
This putative function for a bacterial compass is pure speculation at the moment. But if these bacteria use their magnets primarily to swim down (rather than to find each other, or to do Lord knows what, if anything, in their unfamiliar world), then we can make some testable predictions. Members of the same species, living in natural populations adapted to life at the equator, will probably not make magnets, for here a compass needle has no vertical component. In the Southern Hemisphere, magnetotactic bacteria should display reversed polarity and swim in the direction of their south-seeking pole.
Magnetite has also been reported as a component of several larger organisms, all of which perform remarkable feats of horizontal orientationâthe conventional use of a compass for familiar creatures of our scale. Chitons, eight-plated relatives of clams and snails, live primarily on rocks near sea level in tropical regions. They scrape food from the rocks with a long file called a radulaâand the tips of the radular teeth are made of magnetite. Many chitons make substantial excursions from a living site, but “home” back to the precise spot thereafter. The idea that they might use their magnetite as an orienting compass suggests itself, but the evidence so far offers no support. It is not even clear that chitons have enough magnetite to perceive the earth's field, and Frankel tells me that their particles are mostly above the single domain limit.
Some bees have magnetite in their abdomens, and we know that they are affected by the earth's magnetic field (see article by J. L. Gould, no relation, J. L. Kirschvink, and K. S. Defeyes in bibliography). Bees do their famous dance on the vertical surface of their honeycomb by converting the orientation of their flight to food in relation to the sun into an angle danced with respect to gravity. If the comb is turned so that bees must dance on a horizontal surface, where they cannot express direction in gravitational terms, they become disoriented at first. Finally, after several weeks, they align their dances to the magnetic compass. Moreover, a swarm of bees, placed into an empty hive without cues for orientation, build their comb in the magnetic direction it occupied in their parental hive. Pigeons, certainly no duffers at homing, build a structure made of magnetite between their brain and skull. This magnetite exists as single domains and can therefore function as a magnet (see C. Walcott
et al
. in bibliography).
