The King of Infinite Space (7 page)

Now, point A is at the center of the circle BCD. In his fifteenth, sixteenth, and seventeenth definitions, Euclid has said that given a circle, all of the straight lines from its center to its circumference are equal. From this, Euclid concludes that AC is equal to AB and that BC is equal to BA.

But Euclid has already established that AC is equal to AB. It follows that CA and CB are both equal to AB. Things that are equal to the same thing are equal to one another. This is Euclid's third common notion. It has come in handy, no?

The triangle ACB is thus equilateral.

Done.

S
HORT TO BEGIN
with, Euclid's proof is psychologically shorter than it appears because it makes only one demand of the reader or the student: that he or she recognize that every radius of a given circle is equal to every other radius. The proof is an elaboration of this idea. Euclid has managed perfectly to suggest a powerful machine without doing anything more than racing its motor. Even so, it would be unfair to celebrate this little proof without mentioning a few scruples. “It is surprising,” the contemporary mathematician D. E. Joyce remarked, “that such a short, clear, and understandable proof can be so full of holes.”

Holes? And in Euclid too! Witness the very first step that Euclid takes. His axiom establishes that there exists a unique straight line between any two distinct points, but
there are no points in the proof to come, or anywhere else in Euclid, to anchor the line AB.

The point of intersection C is the source of a second scruple, for why has Euclid assumed that the straight lines AC and BC must share their vertex at C?

Why, for that matter, has Euclid assumed that three equal straight lines must enclose a triangle? To say that the lines are equal is to say one thing; to say that they are the sides of a triangle is to say quite another.

And scruples about construction—they must be added to what is by now an embarrassing list. In constructing two circles, Euclid has apparently withdrawn the point of his compass from point A and then placed it on point B. Nothing Euclid has said has allowed him to lift his compass at all, if only because no compass is ever mentioned in the
Elements
. But in that case, how has Euclid gotten from A to B?

But enough is enough. Purists, stand down. When all is said and done, Euclid's proof does what a proof must do: it compels belief.

Equilateral triangles are unrelieved in their symmetry. They are the same no matter the angle from which they are viewed. They do nothing and go nowhere. No wonder there are so many of these squat brutes hanging around.
The isosceles triangle is altogether more refined. The sides of an equilateral triangle are all equal. The opposite sides of an isosceles triangle are equal, but each base is on its own. The difference is artistically important. Isosceles triangles have the power to soar. Ecclesiastical architects formed an isosceles triangle with their fingertips and joined thumbs to imagine space tapering upward to the vault of a great cathedral.

There is a connection, Euclid establishes very early in the
Elements
, between the sides and the base angles of an isosceles triangle. That there is
some
connection or other between the sides and the base angles of an isosceles triangle—anyone can see that at a glance. But the connection that Euclid affirms is slightly past any point spontaneously ratified by common sense. If two sides of a triangle are equal, then their base angles are equal too. This is a connection more powerful than some connection or other. The sides of a triangle are straight lines and the angles of a triangle pairs of straight lines. There is a kind of governance at work between them, so that the lines impose their equality on the angles that they subtend. This is not something anyone would see at a glance.

Euclid's fifth proposition is often referred to as the Bridge of Asses. The appeal to a bridge reflects Euclid's illustration (
Figure VI.2
), which seems to depict a trestle, but those asses have suggested something else, an intellectual bridge that
schoolroom donkeys are unable to cross. Yet nothing in Euclid's proof justifies its reputation for difficulty. The proof is neither the simplest possible nor the most elegant, but it does offer an appreciation of Euclid in the fullness of his manner. And something else. Euclid's proof reveals an almost perfect coincidence between the illustration of the theorem and the logical steps needed to demonstrate it. Not all of Euclid's proofs are like this, and not all of his illustrations or diagrams are on their face this revealing.

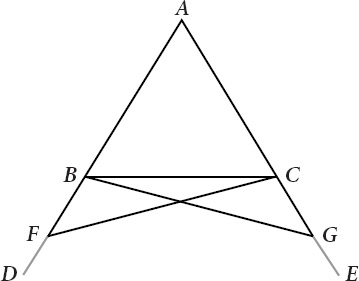
F
IGURE
VI.2.
The Bridge of Asses

“I
N ANY ISOSCELES
triangle ABC,” Euclid affirms, “the angles at the base are equal to one another.” What is more, Euclid then adds, “if the equal straight lines be produced
further then the angles underneath the base will [also] be equal to one another.” The strategy of Euclid's proof is to prove more than what is needed and to take away less than what is proven.

With his original isosceles triangle given in ABC, Euclid constructs a trestle from B to C. Three steps are required for the construction, and some bookkeeping for the argument to come. Euclid first extends the straight lines AB and AC to D and E, respectively. Euclid's second axiom allows straight lines to be extended, and Euclid has just extended two of them.

Permission sought; permission granted.

Euclid then chooses a point F at random on the line BD, and connects the points F and C by the straight line FC. The connection is justified by Euclid's first axiom but the idea of a random choice is an example of Euclid casting out concepts and hoping for the best.

A third step, the last. Choosing a point G on the line AE such that AG is equal to AF, Euclid creates a strut between G and B. His first axiom is in play for the second time. In this, there is nothing strutwise amiss. Yet what justifies the claim that AG is equal to AF? I am glad you asked. Euclid's third proposition affirms that given two unequal straight lines, it is always possible to cut off from the greater a line segment equal to the lesser. AE is the greater line, and AF, the lesser. G is chosen accordingly.

E
UCLID NOW REQUIRES
the assistance of a shady old friend. It is a friend about whom I have already expressed certain reservations, but as Talleyrand said in quite another context, this is no time to be making enemies. Two triangles are congruent, Euclid demonstrated in proposition four, if they coincide in two of their sides and in the angles between them. Using just this proposition, Euclid intends to show that triangles AFC and AGB are congruent. What are friends for?

Already established: AF is equal to AG. There is no need to establish that AB is equal to AC. ABC is, after all, an isosceles triangle. But angle FAG is common to both triangle AFC and triangle AGB. Congruence follows at once, and with congruence, full congress between associated angles. Angle ACF is equal to angle ABG, and angle AFC to AGB.

Again using proposition four, Euclid now shows that BF and FC are equal to CG and GB. But the interior angles BFC and AGB are equal, too. AFC and AGB are congruent, after all. Thus BCF and GBC are congruent as well.

Euclid's conclusion now falls like a ripe peach. Angle FBC is equal to angle GCB, and angle BCF is equal to angle GBC. But the
whole
of angle ABG is equal to the
whole
of angle ACF. Subtracting equals from equals, it follows that the remaining angles ABC and ACB are equal too. These, as Euclid observes with satisfaction, are just the base angles of the isosceles triangle ABC.

Done.

T
HE GREAT MERIT
of Euclid's proof is that it get the job done; its great defect is that it takes so long to do it. The Greek mathematician Pappus provided a proof of the same proposition that is a wonder of efficient elegance. Consider the isosceles triangle ABC and its reflection ACB. The triangle ACB is as close to the triangle ABC as its mirror image. There is in this no surprise. It
is
its mirror image. Whereupon there are a pair of plump reflective identities: AB = AC and AC = AB. Triangle ABC is, after all, isosceles.

And a reminder of what is obvious: angle ABC is equal to angle ACB. It is the same angle.

Therefore, ABC is congruent to ACB, by virtue of Euclid's fourth proposition.

The equality of its base angles follows at once—even faster.

Dulce.

This is lean and cutting as a tooth. But a reservation is in order. Nothing in Euclid's axioms, definitions, or common notions would in the least allow triangles, or any other figures, to be lifted from the plane and reflected back into it.

The Pythagorean theorem affirms that in any right triangle, there is a simple relationship between the length of the
triangle's sides
a
and
b
, and its hypotenuse
h
. It is
a
²
+
b
²
=
h
²
. The sum of the squares of the two sides
a
and
b
of any triangle is equal to the square of its hypotenuse. Known apparently to the Babylonians and made known again by Pythagoras in the fifth century
BC
, the Pythagorean theorem was well known before the ancient world was well worn. On discovering it, Pythagoras on some accounts exclaimed
eureka!
and, on other accounts, sacrificed at once to the Gods. Involving an ox with no interest in geometry, the sacrifice was disgusting, but not so the
eureka
. The theorem's power is obvious. It is grand. In one remarkably limpid statement, it specifies a geometrical relationship among triangles and an arithmetical relationship among numbers. The theorem is powerful enough to compel its converse. Any three numbers
a
,
b
, and
h
such that
a
²
+
b
²
=
h
²
determine a right triangle. This is evidence of some haunting unity between the shapes and the numbers, the distinction between the two an accident of appearance, the result of some symmetry broken long ago or an inadvertence in how they are seen.

It is by means of the Pythagorean theorem that the concept of distance comes under general mathematical control. Some control is needed. Distance is an expanse of some sort, an aspect of geometry. It is also a number of some sort, an aspect of arithmetic. It is one or the other or both or neither. But whatever its nature, distance is the answer to the
question
how far
, one of the great questions of the human race, inferior only, I suppose, to
how much
. Having been expressed as a conclusion about right triangles, the Pythagorean theorem also describes the distance between any two points in the plane because any two points in the plane can be imagined as a pair of triangular fingertips. This is both magical and marvelous—magical because something answering to the unformed idea of an expanse has been assigned a number, and marvelous because the number has been generated by a short, simple symbolic form. Beyond distance measured in two dimensions, there is, as well, distance drumming its fingertips insistently in three dimensions, and, indeed, in any number of dimensions. The noble family of metric spaces all trace their paternity backwards to the Pythagorean theorem.

The symbolic form
a
²
+
b
²
=
h
²
algebraically abbreviates any number of tedious arithmetical facts of the 3
²
+ 4
²
= 5
²
variety. In
a
,
b
, and
h
, it makes use of indeterminate symbols, and in
a
²
+
b
²
=
h
²
, it imposes three arithmetical operations on the numbers that they designate. It took mathematicians a very long time before they could enter into that dizzying world in which such symbols could be handled with easy confidence. They were handled in the ninth, tenth, and eleventh centuries by the great mathematicians of the far-flung Arabic archipelago, but not with easy confidence, and until quite recently, the handling came
hard. Even the greatest of mathematicians had the suspicion that in algebra, as in
The Sorcerer's Apprentice
, symbols they had mastered in one context could prove ungovernable in another.

The apparatus of modern algebra was not available to Euclid. The
Elements
is a treatise of limited symbolic reach. Euclid is content to name points, lines, and various figures in an obvious way, but not once does he step back from the names to consider a more flexible scheme, a more elegant apparatus.

Euclid's proof of the Pythagorean theorem is therefore geometrical. There are no numbers, and no number is squared, but in his geometrical proof, Euclid found a way to convey the arithmetical facts without mentioning them. A great mathematical theorem has many faces. It is one of the ironies of intellectual history that the Pythagorean theorem, which suggests the unity of geometry and arithmetic, should in Euclid's hands receive purely a geometrical proof, almost as if the master could not quite see that in mathematics, as in water, there is never only one side or the other.