The Dancing Wu Li Masters (25 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

Although we cannot perceive the four-dimensional space-time continuum directly, we can deduce from what we already know of the special theory of relativity that our universe is not Euclidean. Here is another of Einstein’s thought experiments.
Imagine two concentric circles, one with a small radius and one with a very large radius. Both of them revolve around a common center as shown.
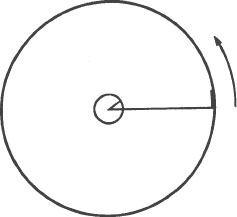
Imagine also that we, the observers, are watching these revolving circles from an inertial co-ordinate system. Being in an inertial co-ordinate system simply means that our frame of reference is at rest relative to everything, including the revolving circles. Drawn over the revolving circles are two identical concentric circles which are in our co-ordinate system. They are not revolving. They are the same size as the revolving circles and have the same common center, but they remain motionless. While we and our nonrevolving circles are motionless, we are in communication with an observer who is on the revolving circles. He actually is going around with them.
According to Euclidean geometry, the ratio of the radius to the circumference of all circles is the same. If we measure the radius and the circumference of the small circle, for example, the ratio of these two measurements will be the same as the ratio of the radius to the circumference of the large circle. The object of this thought experiment is to determine whether this is true or not for both the observers on the stationary circles (us) and the observer on the revolving circles. If the geometry of Euclid is valid throughout the physical universe, as it should be, we should discover that the ratio between the radius and the circumference of
all
the circles involved is identical.
Both we and the observer on the revolving circles will use the same ruler to do our measuring. “The same ruler” means that either we actually hand him the same ruler that we have used, or that we use rulers that have the same length when at rest in the same co-ordinate system.
We go first. Using our ruler, we measure the radius of our small circle, and then we measure the circumference of our small circle. Then we note the ratio between them. The next step is to measure the radius of our large circle and then the circumference of our large circle. Then we note the ratio between them. Yes, it is the same ratio that we found between the radius and the circumference of our small circle. We have proved that Euclidean geometry
is
valid in our co-ordinate system, which is an inertial co-ordinate system.
Now we hand the ruler to the observer on the revolving circles as he passes by us. Using this ruler he first measures the radius of his
small circle and finds that it is the same as ours, since our circles are drawn directly over his circles. Next he measures the circumference of his small circle. Remember that motion causes rulers to contract in the direction that they are moving. However, since the radius of the small circle is so short, the velocity of the ruler when it is placed on the circumference of the small circle is not fast enough to make the effect of relativistic contraction noticeable. Therefore, the observer on the revolving circles measures the circumference of his small circle and finds it to be the same as the circumference of our small circle. Naturally, the ratio between them also is the same. So far so good. The ratios between the radius and the circumference of three circles have been determined (our small circle, our large circle, and his small circle) and they are all identical. This is exactly what should happen according to high-school geometry books across the country. Only one more circle to go.
The observer on the revolving circles measures the radius of his large circle and finds it to be the same length as the radius of our large circle. Now he comes to the last measurement, the circumference of his large circle. However, as soon as he puts his ruler into position to make a measurement on the circumference of the large revolving circle, his ruler contracts! Because the radius of his large circle is much larger than the radius of his small circle, the velocity of the circumference of the large revolving circle is considerably faster than the velocity of the circumference of the small revolving circle.
Since the ruler must be aligned in the direction that the circumference is moving, it becomes shorter. When the revolving observer uses this ruler to measure the circumference of the large revolving circle, he finds that it is larger than the circumference of our large circle. This is because his ruler is shorter. (Contraction also affected his ruler when he measured the radius of his large circle, but since it then was placed perpendicular to the direction of motion, it became skinnier, nor shorter).
This means that the ratio of the radius to the circumference of the small revolving circle is not the same as the ratio of the radius to
the circumference of the large revolving circle. According to Euclidean geometry, this is not possible, but there it is.
If we want to be old-fashioned about it (before-Einstein) we can say that this situation is nothing unusual. By definition, the laws of mechanics and the geometry of Euclid are valid only in inertial systems (that is what makes them inertial systems). We simply don’t consider co-ordinate systems which are not inertial. (This was really the position of physicists before Albert Einstein.) This is exactly what seemed wrong to Einstein. His idea was to create a physics valid for
all
co-ordinate systems, since the universe abounds with the non-inertial as well as the inertial kind.
If we are to create such a universally valid physics, a general physics, then we must treat both the observers in the stationary (inertial) system and the observer on the revolving circles (a non-inertial system) with equal seriousness. The person on the revolving circles has as much right to relate the physical world to his frame of reference as we have to relate it to ours. True, the laws of mechanics as well as the geometry of Euclid are not valid in his frame of reference, but every deviation from them can be explained in terms of a gravitational field which affects his frame of reference.
This is what Einstein’s theory allows us to do. It allows us to express the laws of physics in such a way that they are independent of specific space-time co-ordinates. Space and time co-ordinates (measurements) vary from one frame of reference to another, depending upon the state of motion of the frame of reference. The general theory of relativity allows us to universalize the laws of physics and to apply them to all frames of reference.
“Wait a minute,” we say, “how can anyone measure distance or navigate in a co-ordinate system like the one on the revolving circles? The length of a ruler varies from place to place in such a system. The farther we go from the center, the faster the velocity of the ruler, and the more it contracts. This doesn’t happen in an inertial co-ordinate system, which, in effect, is a system that is at rest. Because there is no
change of velocity throughout an inertial co-ordinate system, rulers do not change length.
“This allows us to organize inertial systems like a city, block by block. Since rulers do not change length in inertial systems, all the blocks that are laid out with the same ruler will be the same length. No matter where we travel, we know that ten blocks is twice the distance of five blocks.
“In a non-inertial system the velocity of the system varies from place to place. This means that the length of a ruler varies from place to place. If we used the same ruler to lay out all the city blocks in a non-inertial co-ordinate system, some of them would be larger than others depending upon where they were located.”
“What is wrong with that,” asks Jim de Wit, “as long as we still can determine our position in the co-ordinate system? Imagine a sheet of india rubber on which we have drawn a grid so that it looks like a piece of graph paper (first drawing, next page). This is a co-ordinate system. Assuming that we are at the lower left corner (we can start anywhere) let us say that a party Saturday night is being held at the intersection marked ‘Party.’ To get there we have to go two squares to the right and two squares up.
“Now suppose that we stretch the sheet of rubber so that it looks like the second drawing.
“The same directions (two squares right and two squares up) still bring us to the party. The only difference is that unless we are familiar with this part of the co-ordinate system, we cannot calculate the distance that we have to travel as easily as we could if all of the squares were the same size.”
According to the general theory of relativity, gravity, which is the equivalent of acceleration, is what distorts the space-time continuum in a manner analogous to our stretching the sheet of rubber. Where the effects of gravity can be neglected, the space-time continuum is like the sheet of rubber before we stretched it. All of the lines are straight lines and all of the clocks are synchronized. In other words, the undistorted sheet of rubber is analogous to the space-time contin
uum of an inertial co-ordinate system and the special theory of relativity applies.


However, in the universe at large gravity cannot be neglected. Wherever there is a piece of matter, it warps the space-time continuum. The larger the piece of matter, the more pronounced the warp.
In the example of the revolving circles, the variation of velocity in different parts of the co-ordinate system caused the ruler to change size. With that in mind, remember that
acceleration (change in velocity) is the equivalent of gravity
. Therefore, changes in the strength of a gravitational field will produce the same contractions of the ruler as changes in velocity. “Acceleration” and “gravity” are two ways of saying the same thing. That means that if a ruler is subjected to gravitational fields of different strength, it changes length.
Of course, it is impossible to travel through our solar system, much less our galaxy, without encountering gravitational fields of varying intensity, which would cause any maps that we somehow could produce to look distorted like the stretched piece of india rubber. The terrain of the space-time continuum in which our earth moves is like a hilly countryside with a mountain (the sun) dominating the geography.
According to Newton, the earth wants to continue forever in a straight line, but forever is deflected from its inclination by the gravitational force of the sun. A balance of the two keeps the earth in orbit around the sun. According to Einstein, the earth’s orbit is simply the easiest path for the earth to take as it moves through the space-time continuum, warped as it is in this neighborhood by the sun.
Imagine how complex is the geography of the space-time continuum which is our universe with its solar systems, star systems, galaxies, and galaxy clusters, each of them causing major and minor bumps, curves, hills, valleys, and mountains in the four-dimensional space-time continuum.
Would it be possible to navigate under such circumstances?
Yes. Although it is a crude example, sailors navigate under somewhat analogous circumstances. We cover the earth with squares which are formed by lines of latitude and longitude. The size of these squares varies depending upon where they are located. The closer they are to the equator, the larger they are. (If this is unclear, look at a globe). Nonetheless, we still can locate physical points on the surface of the earth by designating the intersection of a line of latitude and a line of longitude. Knowing the number of squares between us and where we want to sail does not give us the distance to our destination because the squares may vary in size. However, if we know the nature of our terrain (a globe) we can calculate distances on it (using spherical trigonometry).
