The Crash Course: The Unsustainable Future of Our Economy, Energy, and Environment (6 page)
Read The Crash Course: The Unsustainable Future of Our Economy, Energy, and Environment Online
Authors: Chris Martenson
Tags: #General, #Economic Conditions, #Business & Economics, #Economics, #Development, #Forecasting, #Sustainable Development, #Economic Development, #Economic Forecasting - United States, #United States, #Sustainable Development - United States, #Economic Forecasting, #United States - Economic Conditions - 2009

PART II
Foundation
CHAPTER 5
Dangerous Exponentials
In this book we will explore a few key foundational concepts that will help you gain a better understanding of what lies ahead. None of them is more important than exponential growth.
Exponential growth
holds the honorary position as the “fourth E” in this story. Understanding the ways in which our lives are surrounded and shaped by exponential growth is a necessary part of our ability to effectively anticipate and proactively prepare for our future.
When the president comes on television and says that our highest priority is “returning the economy to a path of growth,” what he is really saying is that our top priority is returning the economy to a path of
exponential
growth. Exponential growth is the only type of growth that is expected and required by our economy.
Examples of exponential growth in your life extend well beyond the economy. We are literally surrounded by examples of exponential growth. The human population has been growing exponentially for thousands of years; consequently, so has humans’ use of resources. This decade there will be exponentially more retail outlets, reams of paper produced, cars on the road, units of energy burned, money created, and food consumed than last decade.
Exponential growth dominates and defines everything that is happening—and that will happen—regarding the economy, energy, and resources of all kinds, which is why you should pay particular attention to this chapter. As soon as you understand exponential growth and can connect it to the other three Es, then you, too, will appreciate why the future will be radically different from the past.
If exponential growth is so ubiquitous and surrounds us at every turn, why is it not completely obvious to everyone? Why do we need to discuss it at all? The reason is that we’re all accustomed to thinking linearly, and exponential growth is nonlinear. We think in straight lines, but exponentials are curved. Here is an example: Suppose I gave you two chalkboard erasers, and asked you to hold them at arm’s length and then move them together at a constant (linear) rate of speed. You would do pretty well at this task, as would most people.
Now let’s repeat the same experiment, but this time we’ll replace the erasers with two powerful magnets. As you move them together, the first part of the journey will progress in a nice, constant fashion, just like with the erasers. But at a certain point—BANG!—the magnets will suddenly draw themselves together and wreck your deliberately even speed. (Let’s hope your fingers were out of the way.)
We could run this experiment a hundred times, and you would never be able to get your body to achieve the same linear control with the magnets as with the erasers. That is because our brains and bodies are wired to process linear forces, and magnets do not exert constant (or linear) force over distance because their force of attraction increases exponentially as they get closer.
Despite our natural affinity for straight lines and constant forces, we
can
still achieve a useful understanding of exponential growth and why it is important. That is what we’re going to do in this chapter.
Exponential growth is not unnatural, but the idea of
perpetual
exponential growth is. We have no models of perpetual exponential growth in the physical world to which we can turn for observation and study. For example, microorganisms in a culture will increase exponentially, but only until an essential nutrient is exhausted, and at that point, the population crashes. Viruses will reproduce and then spread exponentially throughout a population, but they will eventually burn out as their hosts either develop immunity or die off. Nuclear chain reactions caused by neutrons cascading through fissile material are exponential, at least until the resulting explosion forces the material too far apart for the reaction to be sustained.
One thing that we lack here on earth, however, is an example of something growing exponentially
forever
. Exponential growth is always self-limiting and is usually relatively short in duration. Nothing can grow forever, yet somehow that’s exactly what we expect
and
require of our economy. But we will explore more about why that’s the case in a bit.
The Concept of Exponential Growth
What do we mean when we say that something is “growing exponentially”?
To begin with, let’s define “growth.” When we say that something is growing, we’re saying that it’s getting larger. Children grow by eating and adding mass, equities grow in price, and the economy grows by producing and consuming more goods. Ponds get deeper, trees grow taller, and profits expand. Within these examples of growth, we can identify two types.
The first type is what we would call “linear growth.”
Linear
means adding (or subtracting) the same amount each time. The sequence 1, 2, 3, 4, 5, 6, 7 is an example of linear (or arithmetic) growth in which the same number is reliably added to the series at every step. If we add one each time, or five, or forty-two, or even a million, it won’t change the fact that this kind of growth is linear. If the amount being added is constant, then it represents linear growth.
The other type of growth is known as “geometric” or exponential growth, and it is notable for constantly
increasing
the amount of whatever is being added each time to the series. One example is the sequence 1, 2, 4, 8, 16, 32, 64, in which the last number in the series is multiplied by two (or increased by 100 percent) at every step. The amount that gets added in each period is both dependent upon and a little bit larger than the prior amount. In the sequence example given, we see a case where the growth rate is 100 percent. So 2 becomes 4, and 4 becomes 8, and so on. But it doesn’t have to grow by 100 percent to be exponential; it could be any other constant percentage and it would still fit the definition.
Now let’s take a closer look at exponential growth so that we can all be clear about what it is and how it relates to our collective future. The chart below illustrates exponential growth—a chart pattern that is often called a “hockey stick.”
In
Figure 5.1
, we’re graphing an amount of something over time. It could be the number of yeast grown in a flask of freshly squeezed grape juice every 10 minutes, or it could be the number of McDonald’s hamburgers sold each year. It doesn’t really matter what it is or what’s driving the growth; all that is required to create a line on a graph that looks like the curve seen in
Figure 5.1
is that whatever is being measured must grow by some percentage over each increment of time. That’s it. Any percentage will do: 50 percent, 25 percent, 10 percent, or even 1 percent. It doesn’t matter: 10 percent more yeast per hour, 5 percent more hamburgers per year, and 0.25 percent interest on your savings account will all result in a line on a chart that looks like a hockey stick.
Figure 5.1
Linear Growth Compared to Exponential Growth
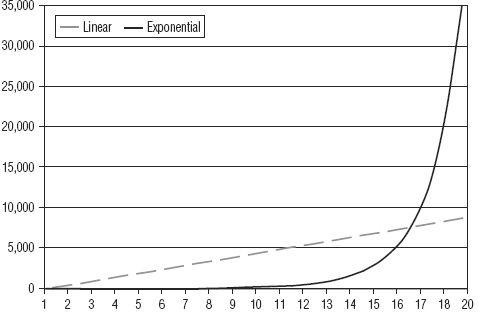
Linear growth is the dotted line; exponential growth is the solid line. The units on both axes are arbitrary; amount is on the vertical (or Y) axis and time is on the horizontal (or X) axis.
Looking at the figure a bit more closely, we observe that the curved line on the chart begins on the left with a flat part, seems to turn a corner (at what we might call the elbow), and then has a steep part.
A more subtle interpretation of
Figure 5.1
reveals that once an exponential function turns the corner, even though the
percentage rate
of growth might remain constant (and low!), the
amounts
do not. They pile up faster and faster. For example, imagine that a long-ago ancestor of yours put a single penny into an interest-bearing bank account for you some 2,000 years ago and it earned just 2 percent interest the whole time. The difference in your account balance between years 0 and 1 would be just two one-hundredths of a cent. Two thousand years later, your account balance would have grown to more than $1.5 quadrillion dollars (more than 20 times all the money in the world in 2010) and the difference in your account between the years 1999 and 2000 alone would have been more than $31 trillion dollars. Where the amount added was two one-hundredths of a cent at the beginning, it was roughly equivalent to half of all the money in the entire world at the end. That’s a rather dramatic demonstration of how the amounts vary over time, but it gets the point across.
Now let’s look at an exponential chart of something with which you are intimately familiar that has historically grown at roughly 1 percent per year. It is a chart of world population; the solid part is historical data and the dotted line is the most recent UN projection of population growth for just the next 42 years.
1
Again I want to draw your attention to the fact that the chart has a flat part, then a corner that gets turned, and then a steep part. By now, it is quite possible that any mathematicians reading this are hopping up and down because of what they might view to be an enormous error on my part.
A first point of departure is that where mathematicians have been trained to define exponential growth in terms of the
rate
of change, we’re going to concentrate here on the
amount
of change. Both are valid, it’s just that
rates
are easier to express as a formula and
amounts
are easier for most people to intuitively grasp. So we’re going to focus on amounts, even though this is not where classical mathematicians would train their logical eyes.
Unlike the
rate
of change, the
amount
of change is not constant in exponential growth; it grows larger and larger with every passing unit of time. For our purposes, it is more important that we appreciate what exponential growth demands in terms of physical amounts than whatever intellectual gems are contained within the rate of growth.
A second point of contention that I expect most mathematicians would vigorously dispute is the idea that there’s a turn-the-corner stage in an exponential chart. In fact, they’re right. It turns out that the point where an exponential chart appears to turn the corner is an artifact of how we draw the left-hand scale. An exponential chart is indeed turning the corner at any and every point along its trajectory. Where that point happens to
appear
on our charts is simply a function of how we scale the vertical axis.
For example, if we take our population chart above, and instead of setting the left axis at 10 billion we set it at one billion (
Figure 5.3
), we see that the line disappears entirely off the chart somewhere around 1850. We can’t see the part after that because it is now way above the top of the chart frame, but in this version of the chart we note that the turn-the-corner event appears to happen around 1900. Instead of having this conversation about turning the corner with population growth right now, it appears as though we really should have had it back in 1900.
Figure 5.2
World Population
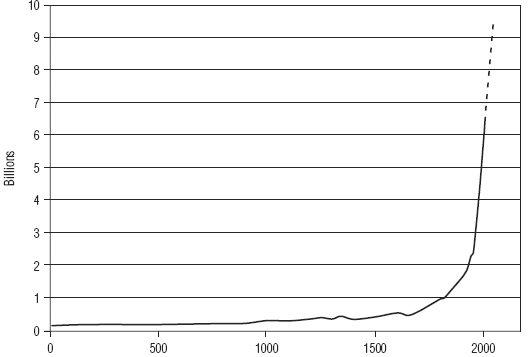
The solid line is historical; the dotted line represents the UN projection.
Source:
U.S. Census Bureau Historical Estimates
2
& U.N. 2004 Projections.
3
