The Code Book (56 page)

The story of quantum cryptography dates back to a curious idea developed in the late 1960s by Stephen Wiesner, then a graduate student at Columbia University. Sadly, it was Wiesner’s misfortune to invent an idea so ahead of its time that nobody took it seriously. He still recalls the reaction of his seniors: “I didn’t get any support from my thesis adviser-he showed no interest in it at all. I showed it to several other people, and they all pulled a strange face, and went straight back to what they were already doing.” Wiesner was proposing the bizarre concept of quantum money, which had the great advantage of being impossible to counterfeit.
Wiesner’s quantum money relied heavily on the physics of photons. When a photon travels through space it vibrates, as shown in
Figure 73(a)
. All four photons are traveling in the same direction, but the angle of vibration is different in each case. The angle of vibration is known as the polarization of the photon, and a lightbulb generates photons of all polarizations, which means that some photons will vibrate up and down, some from side to side, and others at all angles in between. To simplify matters, we shall assume that photons have only four possible polarizations, which we label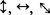 and
and .
.
By placing a filter known as a Polaroid in the path of the photons, it is possible to ensure that the emerging beam of light consists of photons that vibrate in one particular direction; in other words, the photons all have the same polarization. To some extent, we can think of the Polaroid filter as a grating, and photons as matchsticks randomly scattered onto the grating. The matchsticks will slip through the grating only if they are at the correct angle. Any photon that is already polarized in the same direction as the Polaroid filter will automatically pass through it unchanged, and photons that are polarized perpendicular to the filter will be blocked.
Unfortunately, the matchstick analogy breaks down when we think about diagonally polarized photons approaching a vertical Polaroid filter. Although matchsticks oriented diagonally would be blocked by a vertical grating, this is not necessarily the case with diagonally polarized photons approaching a vertical Polaroid filter. In fact, diagonally polarized photons are in a quantum quandary when confronted by a vertical Polaroid filter. What happens is that, half of them at random will be blocked, and half will pass through, and those that do pass through will be reoriented with a vertical polarization.
Figure 73(b)
shows eight photons approaching a vertical Polaroid filter, and
Figure 73(c)
shows that only four of them successfully pass through it. All the vertically polarized photons have passed through, all the horizontally polarized photons have been blocked, and half of the diagonally polarized photons have passed through.
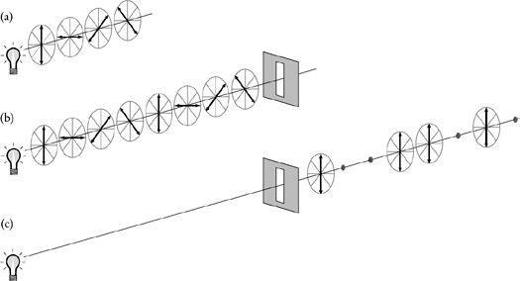
Figure 73
(a) Although photons of light vibrate in all directions, we assume for simplicity that there are just four distinct directions, as shown in this diagram. (b) The lamp has emitted eight photons, which are vibrating in various directions. Each photon is said to have a polarization. The photons are heading toward a vertical Polaroid filter. (c) On the other side of the filter, only half the photons have survived. The vertically polarized photons have passed through, and the horizontally polarized photons have not. Half the diagonally polarized photons have passed through, and are thereafter vertically polarized.
It is this ability to block certain photons that explains how Polaroid sunglasses work. In fact, you can demonstrate the effect of Polaroid filters by experimenting with a pair of Polaroid sunglasses. First remove one lens, and close that eye so that you are looking with just the other eye through the remaining lens. Not surprisingly, the world looks quite dark because the lens blocks many of the photons that would otherwise have reached your eye. At this point, all the photons reaching your eye have the same polarization. Next, hold the other lens in front of the lens you are looking through, and rotate it slowly. At one point in the rotation, the loose lens will have no effect on the amount of light reaching your eye because its orientation is the same as the fixed lens-all the photons that get through the loose lens also pass through the fixed lens. If you now rotate the loose lens through 90°, it will turn completely black. In this configuration, the polarization of the loose lens is perpendicular to the polarization of the fixed lens, so that any photons that get through the loose lens are blocked by the fixed lens. If you now rotate the loose lens by 45°, then you reach an intermediate stage in which the lenses are partially misaligned, and half of the photons that pass through the loose lens manage to get through the fixed lens.
Wiesner planned to use the polarization of photons as a way of creating dollar bills that can never be forged. His idea was that dollar bills should each contain 20 light traps, tiny devices that are capable of capturing and retaining a photon. He suggested that banks could use four Polaroid filters oriented in four different ways (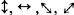 ) to fill the 20 light traps with a sequence of 20 polarized photons, using a different sequence for each dollar bill. For example,
) to fill the 20 light traps with a sequence of 20 polarized photons, using a different sequence for each dollar bill. For example,
Figure 74
shows a bill with the polarization sequence (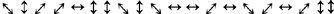 ) Although the polarizations are explicitly shown in
) Although the polarizations are explicitly shown in
Figure 74
, in reality they would be hidden from view. Each note also carries a traditional serial number, which is B2801695E for the dollar bill shown. The issuing bank can identify each dollar bill according to its polarization sequence and its printed serial number, and would keep a master list of serial numbers and the corresponding polarization sequences.
A counterfeiter is now faced with a problem-he cannot merely forge a dollar bill which carries an arbitrary serial number and a random polarization sequence in the light traps, because this pairing will not appear on the bank’s master list, and the bank will spot that the dollar bill is a fake. To create an effective forgery, the counterfeiter must use a genuine bill as a sample, somehow measure its 20 polarizations, and then make a duplicate dollar bill, copying across the serial number and loading the light traps in the appropriate way. However, measuring photon polarizations is a notoriously tricky task, and if the counterfeiter cannot accurately measure them in the genuine sample bill, then he cannot hope to make a duplicate.
To understand the difficulty of measuring the polarization of photons, we need to consider how we would go about trying to perform such a measurement. The only way to learn anything about the polarization of a photon is by using a Polaroid filter. To measure the polarization of the photon in a particular light trap, the counterfeiter selects a Polaroid filter and orients it in a particular way, say vertically, . If the photon emerging from the light trap happens to be vertically polarized, it will pass through the vertical Polaroid filter and the counterfeiter will correctly assume that it is a vertically polarized photon. If the emerging photon is horizontally polarized, it will not pass through the vertical Polaroid filter, and the counterfeiter will correctly assume that it is a horizontally polarized photon. However, if the emerging photon happens to be diagonally polarized (
. If the photon emerging from the light trap happens to be vertically polarized, it will pass through the vertical Polaroid filter and the counterfeiter will correctly assume that it is a vertically polarized photon. If the emerging photon is horizontally polarized, it will not pass through the vertical Polaroid filter, and the counterfeiter will correctly assume that it is a horizontally polarized photon. However, if the emerging photon happens to be diagonally polarized ( or
or ), it might or might not pass through the filter, and in either case the counterfeiter will fail to identify its true nature. A
), it might or might not pass through the filter, and in either case the counterfeiter will fail to identify its true nature. A photon might pass through the vertical Polaroid filter, in which case the counterfeiter will wrongly assume that it is a vertically polarized photon, or the same photon might not pass through the filter, in which case he will wrongly assume that it is a horizontally polarized photon. Alternatively, if the counterfeiter chooses to measure the photon in another light trap by orientating the filter diagonally, say
photon might pass through the vertical Polaroid filter, in which case the counterfeiter will wrongly assume that it is a vertically polarized photon, or the same photon might not pass through the filter, in which case he will wrongly assume that it is a horizontally polarized photon. Alternatively, if the counterfeiter chooses to measure the photon in another light trap by orientating the filter diagonally, say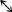 , then this would correctly identify the nature of a diagonally polarized photon, but it would fail to accurately identify a vertically or horizontally polarized photon.
, then this would correctly identify the nature of a diagonally polarized photon, but it would fail to accurately identify a vertically or horizontally polarized photon.
