The Clockwork Universe (22 page)
Read The Clockwork Universe Online
Authors: Edward Dolnick

The answer began with Descartes' graphs. Since steady motion was far easier to deal with than uneven motion, scientists started there. Imagine a man trudging home from work at the end of a long day, dragging himself along at 2 miles per hour. A younger colleague might scoot along at 4 miles per hour. A runner might whiz by at 8 miles per hour.
We could chart their journeys in a table that shows how much distance they covered.

But a graph, Ã la Descartes, makes matters clearer. A steady pace corresponds to a straight line, as we see in the drawing below, and the faster the pace the steeper the line's slope. Slope, in other words, is a measure of speed. (
Slope
is a textbook term with a symbol-laden definition, but the technical meaning is the same as the everyday one. A line's slope is simply a measure of how quickly a situation is changing. A flat slope means no change at all; a steep slope, like a spike in blood pressure, means a fast change.)
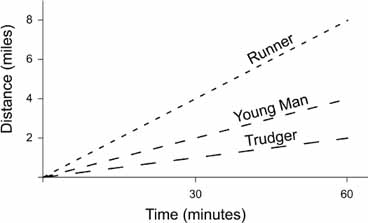
So we can say, with the aid of our picture, precisely what it means to travel at a steady speed of 2 miles per hour (or 4, or 8). It means that, if we were to make a graph of the traveler's path, the result would be a straight line with a certain slope.
This seems simple enough, and so it is, but there is a subtle point hidden inside our tidy graph. The picture has let us dodge a vital but tricky question: What does it mean to travel at two miles per hour
if you're not traveling for a full hour?
Before Descartes came along, such questions had spawned endless confusion. But we have no need to vanish into the philosophical fog. We can nearly do without words and debates and definitions altogether. At least in the case of a traveler moving at a steady speed, we can blithely make statements like, “
At this precise instant
she's traveling at a rate of two miles
per hour
.” All this with the aid of a graph.
But suppose our task was to look at a more complicated journey than a steady march down the street. What does a graph of a cannonball's flight look like? Galileo knew that. It looks like this, as we have seen before.
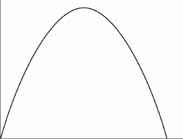
Cannonball's flight
Now our trick seems to have let us down. So long as we were dealing with graphs of straight lines, we'd found a way to talk about instantaneous speed. It was easy to talk about the slope of a straight line, because the slope was always the same. But what does it mean to talk about the slope of a curve, which by definition is
never
straight?
The question was important for two reasons. First, few changes in real life are as simple as the steady
plink plink plink
of drops from a leaky faucet. Second, if thinkers could devise a way to deal with complicated change of
one
sort, then presumably they could deal with complicated changes of
many
sorts. Mathematics is so powerfulâand so difficult for us to learnâbecause it is a universal tool. We balk at algebra, for instance, because those inscrutable
x
's are so off-putting. But algebra is useful precisely because it allows us to fill in the blanks in countless different ways.
A mathematics of change dangled the same promise. Planets and comets speeding across the heavens, populations growing and shrinking, bank accounts swelling, divers plummeting, snowbanks melting, all would yield up their mysteries. Questions that asked when a given change would reach its high point or its lowâwhat angle should a cannon be tilted at to shoot the farthest? when will a growing population level off? what is the ideal shape for the arch of a bridge?
â
could be answered quickly and definitively.
This was a gleaming prize. But how to win it?
The riddle at the heart of the mystery of motion was the question of speed at a given instant. What did it mean? How could you keep from drowning in the whirlpool of “zero distance in zero seconds”?
Answering that question meant learning how to focus on infinitesimally brief stretches of time. The first step was to see that Zeno was not so unnerving as he had seemed. Take his argument that it would take forever to cross a room because it would take a certain amount of time to cross to the halfway point, and then more time to cross half the remaining distance, and so on.

Zeno's paradox. If it takes 1 second to walk to the middle of a room, and ½ second more to walk half the rest of the way, and ¼ second more to walk halfway again, and so on, then it takes
an infinitely long time
to cross the room.
In essence Zeno's argument is a claim about infinity. It seems common sense to say that if you add up numbers forever, and if each number you add is bigger than zero, then eventually the sum is infinite. If you piled up blocks
forever
, wouldn't the stack eventually reach the ceiling, no matter how vast a room you started in?
Well, no, actually, not necessarily.
It all depends on the size of each new block that you added to the stack. If all the blocks were the same size, then the tower
would
eventually reach the ceiling, the moon, the stars. And even if each new block were thinner than its predecessor, a tower might still grow forever.
43
But it might not, if you picked the sizes of the blocks just so.
In modern terms, Zeno's paradox amounts to saying that if you add up 1 +
½
+
¼
+
â
+
1
/
16
+ . . . the total is infinite. Zeno never framed it that way. He focused not on a specific chain of fractions like this one, but on a general argument about what had to be true for
any
endless list of numbers whatsoever.
But Zeno was wrong. If the sum were infinite, as he believed, then it would be bigger than any number you can think ofâbigger than 100, bigger than 100,000, and so on. But Zeno's sum does
not
exceed any number you can name. On the contrary, the sum is the perfectly ordinary number 2.
In a minute, we'll see why that is. But think how surprising this result is. Suppose you took a block one inch high, and put a
½
-inch-thick block on top of it, and then a
¼
-inch-thick one on top of that, and so on. If you added new blocks forever, one a second, through your lifetime and your children's lifetimes and the universe's lifetime, even so the tower would never reach above a two-year-old's ankles.
The taming of infinity represents another of those breakthroughs where a once-baffling abstraction, like “zero” or “negative five,” comes to seem simple in hindsight. The key was to stay relentlessly down-to-earth and never to venture into such murky territory as “the nature of infinity.”
The abstraction that would save the day was the notion of a “limit.” The mathematical sense is close to the everyday one. In one of the Lincoln-Douglas debates, Abraham Lincoln asked his listeners why the Declaration of Independence asserted that “all men are created equal.” Not because the founders believed that all men had already attained equality, Lincoln said.
That
was an “obvious untruth.” The founders' point, Lincoln declared, was that equality for all was a goal that should be “constantly looked to, constantly labored for, and even though never perfectly attained, constantly approximated.”
In the same sense, a mathematical limit is a goal, a target that a sequence of numbers comes ever closer to. The sequence doesn't have to
reach
the limit, but it does have to get nearer and nearer. The limit of the sequence 1, .1, .01, .001, .0001, . . . is the number 0, even though the sequence never gets there. Similarly, the limit of
½
,
¾
, â
,
7/8
,
9
/
10
,
10
/
11
, . . . is the number 1, also never attained. The sequence 1, 2, 1, 2, 1, 2, . . . does not have a limit, because it hops back and forth forever and never homes in on a target.
44
Zeno cast his paradox in the form of a story about a journey across a room. In the 1500s and 1600s a few intrepid mathematicians reframed his tale as a statement about numbers. From that perspective, the question was whether or not 1 +
½
+
¼
+
â
+
1
/
16
+ . . . added up to infinity. Zeno's answer was “yes,” because the numbers go on forever and each contributes something to the sum. But when mathematicians turned from Zeno's words to their numbers and began adding, they found something odd. They began with 1 +
½
. That made 1
½
. Nothing dire there. How about 1 +
½
+
¼
? That came to 1
¾
. Still okay. 1 +
½
+
¼
+
â
? That was 1
7/8
. They added more and more terms and never ran into trouble. The running total continued to grow, but it became ever clearer that the number 2 represented a kind of boundary. You could draw arbitrarily close to that boundaryâwithin one-thousandth or one-billionth or even closerâbut certainly you could never break through in the way that a runner breaks the tape at the finish line.
For the practical-minded scientists of the seventeenth century, this meant the end of Zeno. In the battle with infinity, they declared victory. Zeno had maintained that if it took one second to reach the middle of a room, it would take
forever
to cross to the other side. Not so, said the new mathematicians. It would take two seconds.
Why did that strike them as so momentous? Because when they had taken up the question they truly wanted to answerâwhat does
instantaneous speed
mean?âthey had run head-on into Zeno's paradox. They had wanted to know a hackney coach's speed at the instant of noon and had found themselves ensnarled in an infinite regress of questions of the form,
what was the coach's speed between 12
:
00 and one minute after? between 12
:
00 and 30 seconds after? between 12
:
00 and 15 seconds after? between 12
:
00 and . . . ?
This was the seventeenth-century's counterpart of phone-menu hell (“if your call is about billing, press 1”), and early scientists groaned in despair because the questions continued endlessly, and escape seemed impossible. But now their victory over Zeno gave them hope. Yes, the questions about the coach
did
go on forever. But suppose you looked at the coach's speed in briefer and briefer intervals and found that that sequence of speeds homed in on a limit?
Then your troubles would be over. That limit would be a numberâa definite, perfectly ordinary number.
That
was what “instantaneous speed” meant. Nothing to it. But the greatest mathematicians of antiquity, and all their descendants for another fifteen centuries, had failed to see it.
This was not quite calculus, but it was a giant step toward it. In essence, calculus would be a mathematical microscope, a tool that let you pin motion down and scrutinize it tip to toe. Some moments were more important than othersâthe arrow's height at the instant it reached its peak, the cannonball's speed at the instant it smashed into a city's wall, a comet's speed when it rounded the sunâand, with calculus's help, you could fix those particular moments to a slide and study them close-up.
Or so the newly optimistic mathematicians presumed. But when they grabbed the microscope, they found that no matter how they twisted and tweaked its knobs they simply could not bring the image into focus. The problem, they soon saw, was that everything hinged on the notion of limits, and limits weren't as straightforward as they had thought.
As with all other abstractions, the problem was trying to wrestle with a phantom. What did it mean, precisely and quantitatively, for a sequence of numbers to come very close to a limit? “The planet Mars comes close to the Earth when it is 50 million miles away,” one modern mathematician observes. “On the other hand, a bullet comes close to a person if it gets within a few inches of him.” How close is close?
Even Isaac Newton and Gottfried Leibniz, the boldest thinkers of their age and the leaders of the assault on infinity, found themselves tangled up in confusion and contradiction. For one thing, infinity seemed to come in a disarming variety of forms. In ordinary usage,
infinity
conjured up thoughts of boundless immensity. Now, though, in all this talk of speed at a given instant, it seemed vital to sort out the meaning of “infinitely small” lengths and “infinitely brief” stretches of time, as well.
Worse still, the tiny distances and the tiny intervals of time were all mingled together. Speed means distance divided by time. That was not a problem when you were dealing with large, familiar units like miles and hours. But how could you keep your eyes from blurring when it came to dividing ever-shorter distances by ever-briefer time spans?
No one could think how to classify these vanishingly small times and lengths. Leibniz talked of “infinitesimals,” which were by definition “the smallest possible numbers,” but that definition raised as many questions as it answered. How could a number be smaller than
every
fraction? Perhaps infinitesimals were real but too small to see, like the microscopic creatures Leeuwenhoek had recently discovered? As tiny as they were, infinitesimals were bigger than 0. Except sometimes, when they weren't.
Leibniz tried to explain, but he only made matters worse. “By . . . infinitely small, we understand something . . . indefinitely small, so that each conducts itself as a sort of class, and not merely as the last thing of a class. If anyone wishes to understand these [the infinitely small] as the ultimate things . . . it can be done.” This was, two of Leibniz's disciples acknowledged, “an enigma rather than an explication.” Newton spoke instead of “the ultimate ratio of evanescent quantities,” which was perhaps clear to him but baffling to almost everyone else. “In mathematics the minutest errors are not to be neglected,” he insisted in one breath, and in the next he pointed out that these tiny crumbs of numbers were so close to 0 that they could safely be ignored.
Amazingly, things mostly worked out, much as earlier generations had found that things mostly worked out when they manipulated what were then newfangled and still mysterious negative numbers. In the case of calculus, a seemingly mystical abracadabra yielded utterly down-to-earth, hardheaded results about such questions as how far cannonballs would travel and how much damage they would do when they landed. The very name
calculus
served as a testimonial to the practical value of this new art;
calculus
is the Latin word for “pebble,” a reference to the heaps of stones once used as a calculating aid in addition and multiplication.
Skeptics contended that any correct results must have been due to happy accidents in which multiple errors canceled themselves out. (“For science it cannot be called,” one critic later charged, “when you proceed blindfold and arrive at the Truth not knowing how or by what means.”) But so long as the slapdash new techniques kept churning out answers to questions that had always lain out of reach, no one spent much time worrying about rigor. Leibniz, boundlessly optimistic in personality as well as in his philosophical views, argued explicitly that this gift horse should be saddled and ridden, not inspected. It would all work out.
The muddle would last until the 1800s. Only then would a new generation of mathematicians find a way to replace vague intuitions with clear definitions. (The breakthrough was finding a way to define “limits” while banishing all talk of infinitely small numbers.) In all the intervening years mathematicians and scientists had rejoiced in a bounty they did not understand. Instead they followed the advice of Jean d'Alembert, a French mathematician who lived a century after Newton and Leibniz but during the era when the underpinnings of calculus were still cloaked in mystery.
“Persist,” d'Alembert advised, “and faith will come to you.”
