The Clockwork Universe (16 page)
Read The Clockwork Universe Online
Authors: Edward Dolnick

For nearly twenty years Kepler would stare at Tycho's figures, certain that they concealed a hidden message but for months and years at a time unable to make any headway in deciphering it. He had long since abandoned his geometric models, on the grounds that they simply did not fit the data. The problem was that nothing else did, either.
Kepler knew, for example, how long it took each planet to orbit the sunâMercury, 3 months; Venus, 7 months; Earth, 1 year; Mars, 2 years; Jupiter, 12 years; Saturn, 30 yearsâbut try as he might he could not find a rule to connect those numbers. This was a task with some resemblance to making sense of the numbers on a football scoreboard if you had never heard of football. The number 3 appears sometimes and so do 7 and 14, but never 4 or 5. What could be going on?
Even armed with Tycho's astronomical data, Kepler took six years to find the first two of the three laws now named for him. The story of Kepler's discovery of his laws is a saga of false starts and dead ends piled excruciatingly one upon another, while poor Kepler despaired of ever finding his way.
Kepler's first law has to do with the paths the planets travel as they orbit the sun. Kepler shocked his fellow astronomersâhe shocked himselfâby banishing astronomy's ancient emblem of perfection, the circle. But Tycho's data were twice as accurate as any that had been known before him, and Kepler, who had indulged himself in endless speculative daydreams, now turned the world upside down because of a barely discernible difference between theory and reality. “For us, who by divine kindness were given an accurate observer such as Tycho Brahe,” Kepler wrote, “for us it is fitting that we should acknowledge this divine gift and put it to use.” To take Tycho's measurements seriously meant to acknowledge, albeit slowly and reluctantly, that the planets simply did not travel in circles (or in circles attached to circles or any such variant).
Worn down by endless gruesome calculations, Kepler nearly despaired of ever finding the patterns hidden inside the astronomical records. (He referred wearily to his hundreds of pages of calculations as his “warfare” with the unyielding data). Finally he found that each planet orbits the sun not in a circle but in an ellipse, a kind of squeezed-in circle. This meant, among other things, that the distance from the sun to a planet was not constant, as it would be if the planet traveled in a circle, but rather always changing.
All circles are identical except in sizeâthis was part of what made them perfectâbut ellipses come in infinite variety, some barely distinguishable from circles and others long and skinny. An ellipse is not just an oval but an oval of a specific sort. (To draw an ellipse push two tacks into a piece of cardboard and drop a loop of string around them. Pull the string taut with a pencil and move the pencil along. Each tack is called a focus. The defining property of an ellipse is that, for every point on the curve, if you measure the distance from one focus to the pencil tip and then add to that number the distance from the pencil tip to the other focus, the sum is always the same.
37
)
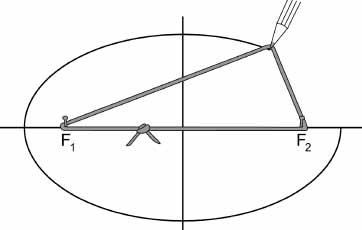
For every point on the ellipse, the distance from F1 to the pencil's tip plus the distance from F2 to the pencil tip is the same.
In the case of the planets, Kepler found, the sun sits at one focus of an ellipse. (The other focus does not correspond to a physical object.) This was Kepler's first lawâthe planets travel in an ellipse with the sun at one focus. This was truly radical. Even Galileo, revolutionary though he was, never abandoned the belief that the planets move in circles.
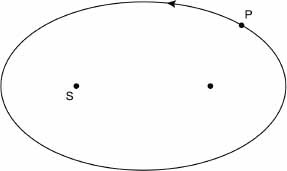
According to Kepler's first law, the planets orbit the sun not in a circle but in an ellipse.
* * *
Kepler's second law was heretical, too. It had to do with the planets' speed as they travel, and it involved another assault on uniformity. The planets didn't travel in perfect circles, Kepler claimed, and they didn't travel at a steady pace, either. The spur was Kepler's belief that the sun somehow pushed the planets on their way. If so, it stood to reason that the force pushed harder when a planet was near the sun and more weakly when it was farther away. When a planet neared the sun, it would race along; when far away, it would dawdle.
It took Kepler two years of false starts to find his second law. (He earned his living, in the meantime, as imperial mathematician to Rudolph II, the Habsburg emperor whose court was in Prague. Kepler's official duties largely centered on such tasks as preparing horoscopes and making astrology-based forecasts of next season's weather or a stalemated war's outcome.) His great insight was finding a way to capture the planets' uneven motion in a precise, quantitative rule. The natural way to describe a planet's motion was to chart its position every ten days, say, and then compute the distance between one point and the next. But that procedure turned out not to reveal any general rule. In a moment of inspiration Kepler saw a better way. The key was to think not of distance, which seemed natural, but of area, which seemed irrelevant.
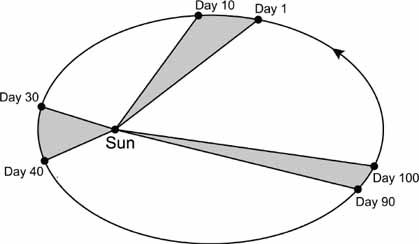
According to Kepler's second law, the triangles (in gray) have different shapes but are identical in area.
Kepler's second law: the line from a planet to the sun sweeps out equal areas in equal times.
Proud of his discoveries though he was, Kepler had no great fondness for these laws, because he had no idea where they'd come from. Why had God not employed circles? Circles were perfect; ovals and ellipses were, Kepler lamented, a “cartload of dung.” And if for some reason He had chosen ovals, why choose ellipses in particular rather than egg shapes or a thousand other possibilities?
Kepler's third law seemed the most arbitary of all, and proved the hardest to find. Kepler's first two laws had to do with the planets considered one at a time. His third law dealt with all the planets at once. Kepler's quest was once again, just as it had been with his Platonic solids model, to find what the various orbits had to do with one another. God surely had not set the planets in the sky arbitrarily. What was His plan?
Kepler had two sets of numbers to work withâthe size of each planet's orbit and the length of each planet's “year.” Neither set of figures on its own revealed any pattern. The size of Earth's
orbit, for instance, revealed nothing about the size of Mars's orbit,
nor did the length of one planet's “year” (the time it took to complete one circuit of the sun) provide any clue to the length of a year on a different planet. Kepler turned his attention to looking at both numbers together, in the hope of finding a magic formula.
The general trend was clearâthe farther a planet was from the sun, the longer its year. That stood to reason, because near-to-the-sun planets had small orbits to trace and distant planets big ones. But it wasn't a matter of a simple proportion. Planets farther from the sun had more distance to cover than closer-in planets
and
they traveled more slowly. It would be as if ships crossing the ocean traveled more slowly than ships hopping along the coast from port to nearby port.
Since he had no idea of the forces that moved the planets, Kepler took on the code-breaking challenge as if it were purely a task in numerology. Like a safecracker armed with nothing but patience, he tried every combination he could think of. If there was no pattern in the lengths of the different planets' years, for instance, perhaps there was a pattern if you took the lengths of the years and squared them. Or cubed them. Or perhaps you could see a pattern if you computed each planet's maximum speed and compared those. Or the minimum speeds. For more than a dozen years, Kepler tried one combination after another. He failed every time.
Then, out of the blue, “On March 8 of this present year 1618, if precise dates are wanted, the solution turned up in my head.” The discovery itself was complicated. Characteristically, so was Kepler's response, which combined gratitude to God, immense pride in his own achievement, and his customary willingness to paint himself unflatteringly. “I have consummated the work to
which I pledged myself, using all the abilities that You gave to me;
I have shown the glory of Your works to men,” he wrote, “but if I have pursued my own glory among men while engaged in a work
intended for Your glory, be merciful, be compassionate, and forgive.”
What Kepler had found was a wayâa mysterious, complicated
wayâto tie the orbits of the various planets together. It required that you perform a messy calculation. Choose a planet, Kepler
said, and then take its orbit and cube it (multiply it by itself three
times). Next, take the planet's year and square it (multiply it by itself ). Divide the first answer by the second answer. For every planet, the result of that calculation will be the same. Kepler's third law is the assertion that if you follow that unappetizing recipe the answer always comes out the same.
Kepler knew, for instance, that Mars's distance from the sun is 1.53 times Earth's distance, and Mars's year is 1.88 times Earth's
year. He sawâsomehowâthat 1.53
Ã
1.53
Ã
1.53 = 1.88
Ã
1.88.
The other planets all told the same story. (Put another way, the length of a planet's year depends not on its distance from the sun, or on that distance squared, but on something in betweenâthe distance raised to the
3
/
2
power.)
But why? What did it mean?
The numbers worked out, which seemed beyond coincidence, but it all sounded like mumbo jumbo. Of all the ways that God might have arrayed the planets and set them orbiting on their way, why had He picked one built around this curious business of squaring and cubing?
The safe door had swung open, but Kepler had no idea why.
Kepler's laws represented a giant advance in decoding God's cryptography, even if he did not know why they were true or what they meant. The next advance came from his fellow astronomer, Galileo, who was almost exactly Kepler's contemporary.
Galileo was born in the same year as Shakespeare, and Galileo's stature in science nearly matches Shakespeare's in literature. “I believe that if a hundred of the men of the seventeenth century had been killed in infancy, the modern world would not exist,” wrote Bertrand Russell. “And of these hundred, Galileo is the chief.” In truth, that seems unlikely. Galileo's genius is beyond dispute, but every great scientist, from Galileo to Darwin to
Einstein, had rivals at his heels. If Shakespeare had not lived,
we would not have “to be or not to be.” If Einstein had not
lived, we might have had to wait a few years for
e = mc
2
.
The same holds for Galileo, great as he was. But Galileo did
shake the scientific world out of its doldrums, and perhaps
Russell was right that no one could have been better suited to that task, either temperamentally or intellectually. Galileo was
brilliant, cantankerous, and expert in wielding all the weapons
of intellectual combat. (Even his hair bristled, as if it, too, were poised for battle.) He spoke wittily and wrote vividly, with a knack for metaphors and homey analogies; he had a flair for mockery, name-calling, and sarcastic put-downs; he had, when he wanted, a honeyed tongue and, as an acquaintance noted, “a way of bewitching people.”
Curiously, Galileo did
not
build on Kepler's work. Indeed, he seems not to have known that Kepler's laws existed at all, even though Kepler had sent him his
New Astronomy
, which included the first two laws and endless astronomical speculation besides. (Galileo put the book away unread.) What Galileo did instead was turn to a completely different part of the cosmic riddle.
Galileo focused on solving a mystery far older than Kepler's. Nearly a century after Copernicus, the question
does the Earth move?
still struck nearly everyone as absurd. Armed with the fame he had earned by turning his telescope to the heavens, Galileo set out to do what Copernicus and Kepler had never done, and what Kepler's laws did not do, eitherâfind a response to the claim that the Earth could not possibly be in motion. Then he set out to tell the world.
Galileo wrote his most important scientific works not in formal, impenetrable prose but in pugnacious dialogues, like miniature plays. He put the arguments of his rivals into the mouth of a character he named Simplicio, the embodiment of intellectual mediocrity. The name perhaps referred to an actual figure, an Aristotelian named Simplicius who lived around a thousand years before Galileo. More likely, Galileo made up “Simplicio” because it was so close to
simpleton
(
sempliciotto
in Italian). Certainly his readers jumped to that conclusion. And one of them, Pope Urban VIII, was notably unamused to find a pet argument of his own put in Simplicio's mouth.
That proved to be a disastrous miscalculation, but a telltale one. Galileo's Italy was a flamboyant place. Showmanship was far more common than bashfulness, and Galileo was never much inclined to hide his talent in any case. Still, he dangerously overestimated his own powers of persuasion. He liked holding forth, about wine and cheese and literature to be sure, but especially about the excellence of the new picture of the heavens and the foolishness of the old view. “He discourses often amid fifteen or twenty guests who make hot assaults upon him, now in one house, now in another,” one friend recalled, after a dinner party, “but he is so well buttressed that he laughs them off.”
To be outnumbered was part of the fun. “If reasoning were like hauling,” Galileo proclaimed, “I should agree that several reasoners would be worth more than one, just as several horses can haul more sacks of grain than one can. But reasoning is like racing and not like hauling, and a single Arabian steed can outrun a hundred plowhorses.”
Galileo not only defended Copernicus against his critics but, in the course of making his argument, devised a theory of relativity. Three centuries before Einstein's version, Galileo's theory proved nearly as hard for common sense to grasp. Inside a room with the curtains pulled, Galileo showed, there is no way to tell if you're standing still or traveling in a straight line at a steady speed. Inside the compartment of a smooth-running new train, to take a modern example, no experiment you can do (short of peeking out the window) will reveal whether you're sitting motionless or racing down the track. You might think that dropping your keys would give the game awayâif the train is moving to the east, wouldn't the keys fall a bit toward the west?âbut in fact they fall straight down, as usual.
More to the point, what is true of a ship or a train is true of the Earth itselfâthere is no way to tell if the Earth is moving or standing still, short of carrying out sophisticated astronomical measurements. No ordinary actions we can carry out reveal whether we're moving. The same holds true for
any
motion that is smooth, steady, and straight, no matter how fast it might be. (The Earth's orbit is nearly circular, not straight, but the circle is so huge, compared to our speed, that any short stretch is effectively a straight line.)
This was a direct attack on Aristotle and all his followers. We can be sure that the Earth does not move, Aristotle had insisted, because we see proof everywhere we look. Rocks fall straight down, not on some curved or slanted path. Buildings don't shake or topple, as they would if the ground beneath them was on the move. A moving world would be chaotic, Aristotle taught, and the most routine task would be as difficult as trying to paint a room while standing on a ladder mounted on wheels.
Galileo showed this was false. Nothing is special about a motionless world. Smooth, steady motion looks and feels exactly the same as utter stillness. The strongest argument against Copernicusâthat he began by assuming something that was plainly ridiculousâwas invalid.
Galileo reached these far-ranging conclusions by means of the humblest experiments imaginable. He began with a metal ball and a wooden ramp. (In time he would add a bucket of water with a hole poked in it.)
Galileo's pet subject was motion, in particular the motion of falling objects. For Aristotle, as we have seen, to be in motion meant to changeâfrom one position to another, perhaps, but also from one “quality” to another, as from “foolishness” to “wisdom.” Galileo was after what looked like simpler game. He wanted to know the rules that govern inanimate objects in free fall. But how could he look closely enough to tell precisely how rocks plummet?
The answer, he decided, was to slow things down. Rather than drop a rock through the air, he would roll a ball down a ramp and hope that what held for the ramp would hold for free fall. This was a nervy move. Arguments by analogy are always risky, and here the analogy seemed far from ironclad. But Galileo, a brilliant teacher and debater, presented this leap of faith as if it were but another step on a casual walk, and his audience leaped with him.
He began by seeing what happened when he let a ball roll down one ramp, across a table, and then up a second ramp. If the two ramps were identical, it turned out, the ball ended up at virtually the same height it had started at. (In the same way, if you let go of a marble in a circular bowl it will roll to the bottom and then up the other side to very, very near its starting height.)
Then came the crucial observation. Galileo chose a second ramp that was less steep than the first one. Once again the ball ended up at the height it had started at, though this time it had to roll farther to get there. Then still another repetition, this time with a second ramp that was only tilted ever so slightly. Again, the ball eventually reached its starting height but it had to roll and roll to get there.
And suppose the second ramp was perfectly flat, not tilted at all? Then, said Galileo, the ball would roll horizontally
forever
.
The flat ramp was a thought experiment, not a real one, but
Galileo proclaimed a new law of natureâany object moving hori
zontally will continue moving horizontally forever, at the same
speed, unless something comes along to intervene. (Newton's first
law of motion is a generalization of the same principle.) Aristotle had decreed exactly the opposite, as we saw earlier. In Aristotle's world, motion was unnatural and always called for explanation; unless a force kept pushing or pulling it, a moving object would always slow and then stop.
We should not downplay Galileo's boldness. In rejecting Aristotle, he was also dismissing what everyone has seen for themselves countless timesâmoving objects
do
always stop. Ignore what all your experience and your common sense have taught you, Galileo said. More important than the world you actually see, more true to the essential nature of things, is an idealized, abstract, mathematical world that you can only see with the mind's eye.
In Galileo's hands, the simple statement that motion was natural had enormous consequences. Here was the key to his theory of relativity and the rebuttal to the Aristotelians' guffawing about a moving Earth. In his day, when roads were rutted and coaches horse-drawn, the most familiar example of smooth travel was on shipboard. What would happen, Galileo asked, if a sailor climbed to the top of the mast and dropped a rock? For Aristotle, this would have been an easy question. If the ship was motionless, at rest in a quiet harbor, the rock would fall straight down and hit the deck at the base of the mast. If the ship was gliding along on a glassy sea, the rock would crash to the deck several inches from the mast. Galileo disagreed. In
both
cases, he insisted, the rock would fall straight down to the base of the mast.
The reason was his first law. The ship, the sailors, the passengers, the rock falling from the mast, are all in horizontal motion, all of them moving together. The rock lands at the base of the mast because mast and rock are both moving horizontally, in unison, at the same time as the rock is hurtling downward.
“Shut yourself up with some friend in the main cabin below decks on some large ship,” Galileo wrote. Bring in some butterflies, a fishbowl with some fish swimming around, a leaky jug dripping water into a pan on the floor. No matter how closely you looked for something out of the ordinary (the fish clustered against one side of their bowl, for instance, or the drops of water missing the pan), Galileo went on, “you could not tell from any of them whether the ship was moving or standing still.”
The same holds for the Earth itself, and all its passengers, as it speeds along on its voyage. The speeding Earth, which races in its orbit at about eighteen miles
per second
, is as safe and solid a home as a ship safely moored at anchor in a mirror-smooth sea.
Even today, Galileo's insight doesn't come naturally. We believe him, though, because we've all carried out countless tests of our own. It sometimes happens, for instance, that we're speeding down the highway, with the car windows rolled up, when we notice a fly buzzing around. The car might be traveling at 70 miles per hour, much faster than any fly can manage, and yet the fly continues unperturbed. Why doesn't the back window slam into it at 70 miles per hour?
Or think about traveling by plane. Drop your phone in a jet and during the fraction of a second it takes to hit the floor, the plane will have traveled perhaps a hundred yards. How is it that it falls at your feet and not a football field behind you? For that matter, how can the flight attendants dare to pour coffee? While the coffee is in midair, on its way to the cup but not yet there, the cup itself will have moved hundreds of feet. How can the crew serve first-class without scalding everyone in economy?
“A company of chessmen standing on the same squares of the chessboard where we left them, we say are all in the same place or unmoved: though perhaps the chessboard has been in the meantime carried out of one room into another.” So wrote the philosopher John Locke in 1690, in one of the earliest discussions of relativity. Whether the board sits on a table or is carried from here to there makes no difference to how the game is played. As for the chess pieces, so for us. Whether the Earth sits immobile at the center of the cosmos or speeds around the sun, all our activities go on in their customary ways.
