The Case for Mars (20 page)

ΔV AND HYPERBOLIC VELOCITY

In this chapter I’ve talked a lot about ΔVs and hyperbolic velocity. The two concepts are not the same, but they are related.

Velocity change, or ΔV (“delta-V”), measured in units of speed, such as kilometers per second (km/s), is the fundamental currency of rocketry. If you have spacecraft with a given dry mass M (i.e., empty of propellant), and a certain amount of propellant, P, and a rocket engine with an exhaust velocity C, the following equation, known as “the rocket equation,” shows how big a ΔV the system can generate:

So the quantity (M + P)/M, known as the vehicle’s “mass ratio,” increases exponentially in proportion to ΔV/C. If ΔV/C = 1, then the mass ratio equals e
¹
= 2.72. If ΔV/C = 2, the mass ratio equals e
²
= 7.4. If ΔV/C = 3, the mass ratio equals 20.1. If ΔV/C = 4, the mass ratio equals 54.6. The exponential is a very strong function; a small increase in ΔV or decrease in C can cause a very big jump in the mass ratio. In fact, the situation is worse than this, because the dry mass M has to include not only the payload you are trying to push, but also includes the mass of the tanks required to hold the propellant and the engines big enough to push the spacecraft with its propellant, and both of these parasitic weights also increase in proportion to P. So as ΔV/C goes up, the mass of the spacecraft goes up faster than the exponential, so much so that depending on the lightness of the structural materials and the density of the propellants employed, somewhere between ΔV/C = 2 and ΔV/C = 3 the mass of a single-stage spacecraft will go to infinity! This is the reason why rocket engineers will kill t get ΔV down and Cup.

By the way, if you’re interested, you can get a rocket’s exhaust velocity in meters per second by multiplying its specific impulse, or Isp, by 9.8. If you want C in units of kilometers per second, multiply the Isp by 0.0098.

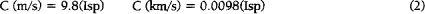
Hyperbolic Velocity, whether in the form of relative velocity departing or arriving at a planet, is not the same as the ΔV, or velocity change, that must be generated by a spacecraft’s rocket engines. However, they are related to each other, and to the maximum reentry velocity of an arriving spacecraft by the equation:

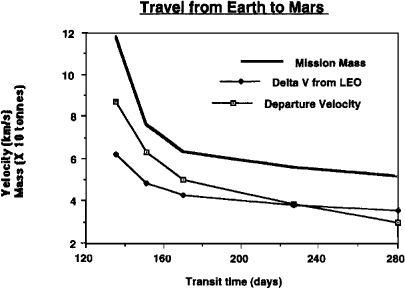
FIGURE 4.3
Relationship between average transit time, departure velocity
, Δ
V, and spacecraft mass for a 20-tonne spacecraft leaving low Earth orbit (LEO) for Mars. Spacecraft propulsion is hydrogen/oxygen with a specific impulse of 450 seconds. Note that mission mass rises steeply for transits less than 170 days.

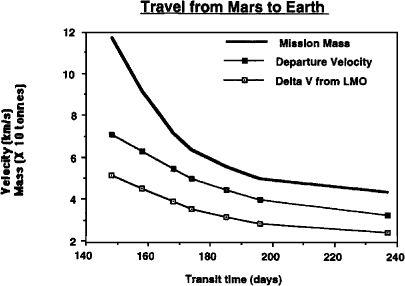
FIGURE 4.4
Relationship between transit time, departure velocity, ΔV, and spacecraft mass for a 20-tonne spacecraft leaving low Mars orbit (LMO) for Earth. Spacecraft propulsion is methane/oxygen with a specific impulse of 380 seconds. Note that mission mass does not begin to rise sharply until you attempt to reduce transit times below 170 days.

where V
_o
is the velocity of the spacecraft at the lowest point of the departure orbit, ΔV is the velocity change exerted by the spacecraft’s rocket engines, V
_e
is the planet’s escape velocity (11 km/s for Earth, 5 km/s for Mars), V
_h
, is the spacecraft’s hyperbolic velocity, and V
_r
is the reentry velocity. In
Figures 4.3
and
4.4
we show the relationships between transit time, departure velocity (or “hyperbolic velocity”), ΔV, and mission mass for 20-tonne spacecraft leaving low orbit about either Earth or Mars to make an interplanetary transit.

5: KILLING THE DRAGONS, AVOIDING THE SIRENS

In olden days, before the Earth was well explored, map makers used to decorate unknown regions of their maps with various imaginative creations, not the least of which were menacing dragons that could swallow a ship whole, and delightful but equally dangerous Sirens who could lure sailors to wreck on rocky shores by the temptation of their sweet songs. The dragons may have been imaginary, but even imaginary dragons can and did prey upon the minds of would-be voyagers, and by so doing stifled human exploration for centuries. And Sirens never did need to be real in order to be heard, and heard they were, drawing many a hopeful venture fatally off course.

Well, things haven’t changed that much. Today those who hope to raise a mission to Mars find their charts filled with dragons too. Reports of horrible beasts with names such as Radiation, Zero-G, Human Factors, Dust Storms, and Back Contamination intrude into the discussion of mission plans, and do their worst to terrorize would-be crews (unsuccessfully), ould-be mission planners (somewhat successfully), and would-be mission sponsors (very successfully). A Siren is there too, named Diana, the Moon Goddess, and her songs can be heard calling the Martian mariners to divert their ships once more to a barren destination. If we’re going to get to Mars, we’re going to have to clear the maps. The dragons, Cyclops, and other monsters of the mind must be ki
lled, and the Siren exposed for the fraud she is.

RADIATION HAZARDS

One of leading dragons barring the path to Mars goes by the name Radiation. Radiation is deadly, we are told, and only by using ultra-fast spacecraft that can speed through the supposedly radiation-infested seas of space in impossibly short times can we be sure of a safe voyage. Or alternatively, we are told that only by using huge spacecraft with masses approaching those of asteroids can we shield the crew well enough to assure their health. We are further warned that cosmic radiation is something totally new in character, and only after we have spent decades studying its long-term effects on humans in interplanetary space can a trip to Mars be risked.

But in fact, almost all the assertions quoted in the above paragraph are sheer nonsense. The only one of them that is even close to being true is the first, that “radiation is deadly”—which it certainly is, but only if taken in excessive quantities.

Human beings have evolved in an environment featuring a significant amount of natural background radiation. In the United States today, people who live near sea level receive an annual radiation dose of about 150 millirem. (A millirem is a thousandth of a rem, the basic unit used to measure radiation doses in the United States. Europeans use Sieverts. One Sievert equals 100 rem.) Those who can afford to live in Vail or Aspen, on the other hand, take an annual dose of more than 300 millirem in consequence of their willingness to forgo a significant fraction of the cosmic ray shielding offered to them by the Earth’s atmosphere. Because we have evolved in a radiation field, humans actually need radiation to stay healthy. It may be counter to popular belief and the orientation of various governmental regulatory agencies, but numerous studies of individuals subjected to an unnaturally radiation-free environment have shown significant health deterioration relative to controls exposed to natural levels of ionizing radiation. This phenomenon, known as hormesis
⁹
,
¹⁰
, is
caused by the fact that the human body needs a ce
rtain amount of pummeling by natural radiation in order to keep its self-repair mechanisms stimulated. It is unclear what the optimum radiation expos
ure level for human health is, but it is not zero.

That said, it is certainly true that very large amounts of radiation delivered over very short amounts of time, such as the exposure to a huge dose within seconds via the gamma-ray flash from an atomic bomb blast, or within minutes by exposure to unshielded release products from a disabled nuclear reactor, can and will kill. The effects of such prompt doses of radiation are well-known from studies of the victims of the Hiroshima and Nagasaki bombings. These studies have revealed that prompt doses of less than 75 rem result in no apparent health effects. If the doses are between 75 and 200 rem, radiation sickness (whose symptoms are vomiting, fatigue, and loss of appetite) will appear in from 5 percent to 50 percent of exposed individuals, with the percentages increasing from the low to high end of this range as the dose increases from 75 to 200 rem. At this level of exposure almost everyone recovers within a few weeks. At 300 rem, radiation sickness is unal, and some fatalities start to appear, rising to 50 percent at 450 rem and 80 percent at 600 rem. Almost no one survives doses of 1,000 rem or more.

These, however, are the effects of prompt doses, which is to say doses that occur on a time scale much shorter than the weeks-to-months time scale for cellular reproduction and bodily self-repair. The situation is much like drinking alcohol or any other chemical toxin. A man could drink a martini a night for years and suffer no obvious ill effects, his liver having adequate time to cleanse his body after each drink. Drinking a hundred martinis in a single night, though, would kill him. Similarly, radiation causes damage to living organisms by inducing chemical reactions within cells that create toxic substances that can kill or otherwise derange individual cells. Below a certain dose rate, the self-repair capabilities of individual cells can act fast enough to reject the radiation-induced toxin and save the cell. At significantly higher rates, human body tissues acting as a whole are able to generate replacement cells for those that have become casualties, before the loss of those cells causes problems for the body as a whole. It is only when dose rates occur at a pace that overwhelms these self-repair mechanisms that severe health impacts occur.