The Australian Ugliness (29 page)

Vitruvius scrutinized his fellow men more closely to find further evidence of harmonic pattern. He was delighted to discover that their frames carried a network of mathematical divisions: ‘The human body is so designed by nature,' he wrote in Book III, ‘that the face from the chin to the top of the forehead and the lowest roots of the hair, is a tenth part of the whole height; the open hand from the wrist to the tip of the middle finger is just the same, the head from the chin to the crown is an eighth, and with the neck and shoulder from the top of the breast to the lowest roots of the hair is a sixth…' and so on. Furthermore the face is a veritable graph: ‘The distance from the bottom of the chin to the underside of the nostrils is one third of it, the nose from the underside of the nostrils to a line between the eyebrows is the same; from there to the lowest roots of the hair is also a third comprising the forehead…The other members too have their own symmetrical proportions.'

It is difficult to believe that such wishful thinking ever could have commanded a sizeable body of artistic thought. If the proportions stated for the body or the face were exact everyone would look alike. If they were intended to be only approximate, then they mean nothing as a rule for design, since it is the subtle little differences in proportion which express major differences of character in the human design. And if the ancients were not considering ordinary mortals but only an ideal, a perfect human, a god, then who among the artists are we to follow? Where is the perfectly proportioned human on which we can base our proportions of building? No doubt he is an athlete, tall, trim and bronzed, poised against the blue sky of ancient Greece, or perhaps a modern Olympic competitor. Western, of course; Caucasian and all that, and male. The Vitruvian figures were always male, sometimes aggressively so.

Illogical as it is, the belief that the elusive ‘perfect' human body holds a secret of universal proportional beauty was carried high through the Renaissance and appears triumphant again today in the roguish figure with which Le Corbusier embellishes his measuring stick
Le Modulor
.

As already mentioned, Le Corbusier proposed
Le Modulor
after the Second World War as a method of standardizing and ‘harmonizing' dimensions of all manufactured goods, while reducing the obstacle created by the irreconcilable metric and foot-and-inch systems, which are now splitting the world. It takes the form of a graduated scale, a useful tool for draftsmen, and is based not on the repetition of even units— inch upon inch—but on a logarithmic progression of lengths. Starting at a basic dimension of 2.26 metres, the intervals diminish in steps of even proportion towards zero, and in the other direction (beyond the length of the rule) enlarge in the same progression towards infinity.

The basic dimension of 2.26 metres was selected by Le Corbusier as being the height of a man standing with one arm raised. He proposed this as a standard dimension for the ceiling height of rooms, a measurement based on the human being rather than the arbitrary inch or metre. The man whose arm is raised is taken to be six feet tall. In earlier experiments with
Le Modulor
, Le Corbusier recounts that he and his collaborators had adopted a human height of 1.75 metres, but this was not proving satisfactory in some of the practical details of conversion to feet and inches. Then one draftsman suggested: ‘Isn't that rather a French height? Have you ever noticed that in English detective novels, the good-looking men, such as the policemen, are always six feet tall?' So they amended the basic measurement to 1.8288 metres (6 feet) and this solved their problem.

Le Corbusier was not prepared to leave this measuring stick at the utilitarian level. Having selected rationally if not very scientifically a basic dimension keyed to human scale, he diverted to the mystic ‘mathematics of the human body, gracious, elegant and firm'. In the body he expected to find, as the Ancients did, ‘the source of that harmony which moves us: beauty'. On the measuring instrument he drew in his familiar easy scrawl the outline of a man—the English policeman, presumably—with one enormous hand raised above his head to the 2.26 metre line. He discovered that the figure could be divided vertically into sections of pleasing mutual relationship. He used the navel, not as a socket for the point of a pair of compasses, but to mark one of the ‘decisive points' of the human body's occupation of space. As he shows it, the policeman's navel is conveniently situated half-way between his toes and raised fingers. This central position of the navel, as noted by Vitruvius, may apply universally to athlete, policeman, giant, or pigmy, because all proposals of this sort avoid specifying whether the raised arm should be stretched or bent, and any differences may be adjusted at the elbow.

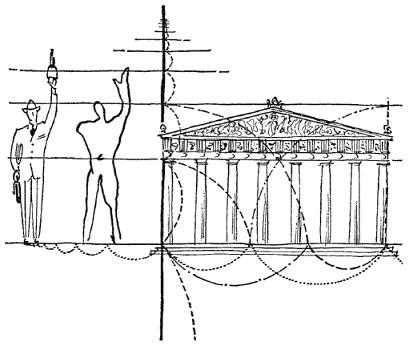
Le Corbusier then took three ‘decisive' dimensions from the figure of his policeman, measuring from ground to the navel, to the top of the head and to the raised fingertips, and from these three he developed the entire system of
Le Modulor
. By combining two simple mathematical progressions, a range of dimensions was obtained from 2.26 metres (basic ceiling height) descending in decreasing steps to the smallest measurable size. It was intended that a tape so graduated should be at hand on every drafting board, eventually supplanting the foot or centimetre rules. It could eliminate arbitrariness in the subdivisions of building. The architect or draftsman, after being led by functional requirements to an approximate dimension for any detail— for instance the height of a sill—would consult the tape and select the nearest
Modulor
size. As all
Modulor
sizes are linked in a progression, the dimensions of the building would be linked or ‘harmonized' to each other and to human scale.

While Le Corbusier was careful to explain that this measuring tape did not relieve the artist of any responsibility, while he reserved for the artist the right to make a ‘personal interpretation' of the proportions which it suggests, still he claimed that
Le Modulor
would help a draftsman to select the most pleasing proportions not only for the parts of architecture, but indeed for sculpture or painting as well. He was naturally delighted when Albert Einstein wrote: ‘It is a scale of proportions which makes the bad difficult and the good easy.' Durisol Inc., a company in New York, undertook in 1947 to market
Le Modulor
as ‘a scale for harmonic measurement of space', and Le Corbusier saw himself entering the country of numbers, ‘
passe la porte des miracles
'.

Anyone else is entitled to select other key features of the human frame—for example the joints: knees, pelvis and shoulders—and claim for them more decisive roles in the body's occupation of space than that enjoyed by the immobile navel. A different scale could thus be drawn up from the relative positions of these features, no less logically related to the body. Someone else may prefer to base a system on the proportions of the width of a policeman to his height. A dozen different systems of proportioning could be devised on the results of a brief run over a human body with a tape-measure. But of all the possible points of reference and combinations of dimensions, Le Corbusier was led by his practised artist's eye direct to the one set of proportions which accorded to the classical designer's golden rule; he selected a division approximating the mathematician's extreme and mean ratio, the traditional conception of perfection in proportion, the Golden Section.

If the rational movement in architecture cannot accept any mystical connection between the figure of a man and a divine system of proportion, it is nonetheless as impressed by mathematicians as any aesthetician of antiquity. In
Architectural Principles in the Age of Humanism
Professor Wittkower went some way towards presenting a disenchanted post-war generation of architectural students with a creed. Many saw a new direction for a Functionalism that had lost its way as they followed him through the historic progression of the idea that architecture, in the company of the musical scale, may reach through a system of mathematical ratios finally to the being of God himself. Wittkower traced the growth of number symbolism and mysticism from the Pythagorean conceptions (for example: ‘Three is the first number because it has a beginning, middle and end. It is divine as the symbol of the Trinity') through Plato's suggestion that cosmic order may be obtained, and the harmony of the world expressed, in a pyramidal lambda of the figures 1, 2, 3, 4, 8, 9, 27 (‘the ratios between these numbers contain not only all the musical consonances but also the inaudible music of the heavens and the structure of the human soul'). Renaissance architects, practical men, converted the heritage of harmonic theories into workaday techniques. They modified the strict classical modular system and developed new codes. Palladio in the mid sixteenth century gave a general rule to harmonic proportions for the height of rooms in relation to their width and length. ‘A wall [was] seen as a unit which contains certain harmonic potentialities,' said Wittkower. ‘The lowest sub-units, into which the whole unit can be broken up, are the consonant intervals of the musical scale, the cosmic validity of which was not doubted.'

Gradually the search for a key to the cosmic harmony was abandoned, but the belief in the existence of a universal beauty and a science of proportions lingered on into the middle of the eighteenth century. Then a new tide of rationalism engulfed it with the cold water of the ideas that architecture and music are not comparable since they communicate with the mind through different organs, and that architecture and mathematics operate on different levels: note how a building's apparent proportions change as the observer moves about. The effects of proportion depend on the association of ideas, not an abstract reason, and are relative to the beholder, his nature, his time and his place. Thus Burke, Kames, Knight and others argued in the eighteenth and nineteenth centuries, and in the twentieth a leader of the modern movement restated the most obvious objection to all golden rules: ‘Beauty is relative because men are different,' said Piet Mondrian, a painter for whom an utmost delicacy of proportioning in lines, spaces and solids constituted the very means of expression. ‘Attachment to a merely conventional conception of beauty hinders a true vision…'

For two centuries, then, bridging across generations of the picturesque, the romantic, the worldly, and deep into the revolution of the functional, the thought of universal harmony lay dormant. Men with all kinds of conflicting artistic approaches could agree at least on one principle: whatever the style, art was a task for artists and not for mathematicians; it was an understanding between an artist and an observer; it was in the eye that received a satisfying message.

But the closed door of the mathematician's study slowly regained its fascination for the architect. Everything he saw through the keyhole as the twentieth century developed suggested analogies with the problems of his own creative work. When the mathematician advanced in his studies of three-dimensional geometry the designer saw new prospects in plastic forms, and when the mathematician directed his attention to a fourth dimension the architect could scarcely contain himself. Hence the world-wide enchantment of the title which Sigfried Giedion attached to his famous account of the origins of the modern movement:
Space, Time and Architecture
.

Many architects today still respond to an old magic and look to their profession for somewhat more than creative satisfaction. The polite apathy which the ordinary cultivated layman extends to architecture is counter-balanced by a high intensity of feeling on a certain thin professional stratum from which architecture is viewed not simply as the ultimate art of man, for this much is self-evident, but also as a dazzling light now shaded by ignorance, a saviour of mankind's soul—not to mention his body. On the day when all building accords to the cosmic harmony, all men will live in order and peace of mind. The secret of the harmony escapes us temporarily, but who can deny that the Greeks were close to it on the Acropolis?

Thus the search for inspiration in numbers is revived, if on a somewhat less emotional plane, and linked now to the technological demand for an international module to reconcile the metric and foot- and-inch systems and to facilitate the prefabrication and international exchange of parts. High-level meetings of professional men and technicians in Italy and England have discussed the physical details while aestheticians re-examine the complex arithmetic which the Greeks brought to perfection in the Parthenon. The geometry of the medieval mason is drawn out into the daylight. Even Chartres Cathedral's asymmetrical facade is found, by Professor Levy of Massachusetts Institute of Technology, probably to be following a mathematical ‘melody' of dimensions based on an octagonal whorl in the Gothic section and a modular scale in the Romanesque part.

Le Corbusier was never alone in his experiments with
Le Modulor
. Once again he was leading his profession, this time in the revival of a concept and an argument which had been discredited for two centuries: the concept of an objective system of beauty which may be applied to all men's construction. But what made his invention profoundly significant as an architectural development in the middle of the twentieth century was that it returned, beyond the numbers, to the dawn of philosophy to try to find some sort of mysterious link for the system with the proportions of the body, some hint of divine inspiration. The sheer reaction of these suggestions coming from one of the spiritual leaders of twentieth-century architecture might have been expected to take the rational movement's breath away. Instead, thousands of Le Corbusier's disciples round the world began to play with
Le Modulor
and to claim to see some part of the miracle which the inventor himself all but experienced. Some criticism was made at the time of inherent difficulties in the practical application of the scale, but there was no sign of shock; only a movement which had retained its rational principles would have been shocked.