Secrets of Antigravity Propulsion (47 page)

Before carrying out a retest, we constructed a photo-relay circuit that would reverse the sawtooth-wave polarity to the capacitor.
Thus, by operating a switch in the adjoining observation room, we could momentarily turn on a room light and activate the photo-relay circuit to reverse the capacitor polarity without actually touching the apparatus.
Pappas also set up a video camera on the ceiling that looked down on the capacitor rotor so we could view any movement of the apparatus remotely from the observation room.
This was done to minimize the chance that air currents produced by movement of people in the room or by their breathing would disturb the apparatus.
We found that it would take at least an hour for the swinging of the apparatus to subside, and even then oscillations would still be present due to room drafts.
We energized the capacitor with a 1.5-megahertz RC-Norton wave, remotely reversing the waveform polarity on the capacitor, but we saw no comparable reversal or alteration in the swing of the apparatus.
We concluded that no gravitational-thrust effect on the rotor could be seen other than the rotor’s ongoing slow oscillations arising from room drafts.
Using a makeshift tensometer, I determined that if the capacitor was able to develop a gravitational force of at least 0.04 percent g, a persistent rotary movement of the apparatus should have been observed.
The null result, then, calls into question claims that low-voltage waveforms are able to induce gravitational thrusts on capacitors.
Later, Pappas modified the rotor assembly so that the sawtooth-wave generator was supplied with 16 volts DC via fine feed wires attached to the rotor’s suspension wire, with the power switch being situated in the observation room.
In this way, we were able to turn the wave generator on and off from our remote location.
We also deactivated the polarity-reversing relay to omit any vibrations that arose when the relay was energized.
After allowing several hours for the apparatus to equilibrate, power was turned on and later turned off, but no thrust could be seen other than the swings arising from room drafts.
Naudin reported that he had duplicated the Dimitriou capacitor rotor experiment and had observed a 1-degree rotation of the apparatus.
Our rotor was constructed in a fashion similar to that of Naudin’s except our capacitor plates were made from sheet copper instead of sheet aluminum and we activated only one of the two rotors.
Based on our results, we are left to wonder whether the 1-degree rotation Naudin reported was due to air currents and not to a true detection of gravitational thrust.
In his description of the experiment, Naudin acknowledged that air currents could pose a problem to the stability of the capacitor rotor arm.
Dimitriou’s original rotor experiment used capacitors that were much more massive than those used in our experiment, since they each incorporated a 1-centimeter-thick copper slab.
Thus, the rotor experiment should be repeated using copper slabs of similar thickness to see if a positive result is obtained.
Another experiment that should be duplicated is a rotor experiment that Dimitriou demonstrated to professors at the University of Manchester.
In that case, two 1.5-centimeter-diameter mica capacitors were placed at opposite ends of a 25-centimeter rod that was suspended at its center.
When energized with an RC-Norton waveform, the arm reportedly rotated 20 degrees.
Dimitriou has developed a working theory that has guided his experimental discoveries, details of which are given in his master’s thesis.
He makes a number of deductions from conventional electrostatic and gravitation theory that have led him to assume an equivalence between the rate of change of a capacitor’s charging current and a gravitational acceleration acting on the capacitor.
Alternatively, he formulates this as a relationship between an accelerating rate of change of a capacitor’s electric field intensity and a consequent gravitational acceleration acting on the capacitor.
As shown in the text box below, his electrogravitic acceleration relationship (13) is in agreement with the subquantum kinetics prediction of how virtual charge induces gravitational force given by equation 8 in chapter 4.
Equivalence of the Dimitriou Electrogravitic Theory with That of Subquantum Kinetics
Dimitriou assumes that a constant current,
i
, producing a constant rate of change of charge, dQ/dt, on a capacitor should be equivalent to effecting a proportionate state of motion in the capacitor and inducing its movement at a constant velocity, v, relative to the charge’s frame of reference, mathematically expressed as:
i
=
(
dQ
)/(
dt
)
∝ −
v
Alternatively, given that a constantly charging current will produce a constant increase in the rate of change of electric field intensity, d
E
/dt, he states that this rate of increase should be equivalent to a proportionate state of motion at velocity, v, expressed as:
i
=
ε
S
(
d
E
)/(
dt
)
∝ −
v
in which
ε
is the dielectric constant of the capacitor and S is its surface area.
Note that electric field intensity is the same as the negative of the voltage gradient across the capacitor (i.e.,
E
=
–
∇
φ
E
).
Thus he posits that a linear increase in charge on a capacitor plate, or linear increase in voltage gradient across a set of capacitor plates, is equivalent to a virtual velocity vector directed toward the capacitor’s positive pole, but that this does not result in any acceleration or motional displacement of the capacitor.
Further, Dimitriou deduces that the rate of change of current, di/dt, producing an accelerating change in the amount of charge on a capacitor, d
2
Q/dt
2
, or an accelerating change in the electric field intensity across the capacitor plates, d
2
E
/dt
2
, should be equivalent to effecting a state in which the capacitor behaves as though it was subject to a gravitational acceleration,
a
g
, expressed as:
(
di
)/(
dt
)
=
(
d
2
Q
)/(
dt
2
)
=
ε
S
(
d
2
E
)/(
dt
2
)
∝
a
g
Thus, he supposes that an accelerating increase in charge on a capacitor plate, or accelerating increase in voltage gradient across a set of capacitor plates, is equivalent to an acceleration of the capacitor toward its positive pole.
He presumes that exertion of a gravitational force and displacement of a capacitor occur only in situations of the second kind, as in equation 12, in which the capacitor’s electric field intensity increases or decreases nonlinearly with time.
On the assumption that the electric field intensity is conceived as a wave traveling at the speed of light and that its amplitude changes with distance in the same manner as it changes with time, equation 12 may be expressed in terms of the change of electric potential with respect to distance, r, rather than with respect to time, t, as follows:
ε
(
d
2
E
)/(
dr
2
)
=
ε
(
d
2
)/(
dr
2
)
(
∇
φ
E
(
r
)
)
=
ε
∇
(
∇
2
φ
E
(
r
)
)
∝
a
g
in which
E
= –
∇
φ
E
.
Given that
a
g
=
F
g
/m, this may be seen to be identical to equation 8, the subquantum kinetic coupling relation derived in chapter 4 that expresses the electrogravitic effects of virtual charge densities.
Dimitriou’s theory relates electrogravitic acceleration to charging current, which is advantageous from an electrical engineering standpoint since the output of a wave generator is often described in terms of the current it generates.
Subquantum kinetics, however, has the advantage of offering a conceptual model that allows one to see what might be going on to cause there to be this electrogravitic linkage.
It allows one to see the connection between electric field potential, virtual-electriccharge density, gravity field potential, and gravitational acceleration.
Subquantum kinetics also shows that a first derivative of electric field potential may also be important in the high-frequency regime.
It is interesting that Dimitriou arrived independently at an experimentally based formulation that is equivalent to the electrogravitic formulation of subquantum kinetics.
In summary, further research is needed to check out Dimitriou’s findings.
I believe that an electrogravitic thrust effect should exist, but at wave voltages much higher than the ones Dimitrou and Naudin were using.
Additional experimentation with sawtooth waves in the kilovolt range should hopefully bring this electrogravitic thrust phenomenon up to a detectable level.
Similarly, additional experiments should be conducted to excite Dimitriou’s disc antenna with RF in the kilovolt range to determine with greater certainty whether gravity screening is produced.
12
HIGH-VOLTAGE ELECTROGRAVITICS EXPERIMENTS
Investigations into electrogravitics have continued outside of the classified world as amateur researchers, inspired by Brown’s work, have striven to reproduce his results.
Experiments conducted by a few researchers are reviewed below.
The reader should be aware that one takes a considerable risk when working with high voltages, since high-voltage power supplies can deliver lethal shocks.
Thus, it is not recommended that people undertake these experiments unless they are thoroughly familiar with the hazards involved and have taken proper safety precautions.
12.1 • TOM TURMAN’S ELECTROKINETICS EXPERIMENTS
Electrical engineer Tom Turman’s initial inspiration to do research in electrogravitics came after reading a 1958 article by Gaston Burridge about Brown’s work.
In an attempt to duplicate some of Brown’s flying-disc experiments, Turman conducted private electrogravitics research between 1965 and 1972, while studying electrical engineering at Texas Tech University.
In 1968, he began corresponding with Brown, both by telephone and by letter.
He told Brown about the experiments he was performing and asked if Brown could clarify some aspects of his flying-disc experiments.
Brown was impressed with Turman’s independent work and at one point was seriously considering hiring him as his assistant.
Unfortunately, circumstances did not permit him to follow through.
Turman did not have university funding to help him carry out his research.
Most of the equipment he acquired for his task was either given to him or purchased at a low price from electrical surplus dealers and subsequently reconditioned.
He had a homemade power supply capable of delivering 300 kilovolts DC at up to 100 milliamperes, an eight-channel oscillograph for use in measuring voltage, current, and force, and a capacitance-type gauge capable of measuring small changes in the weight of a suspended electrogravitic test device.
Turman built several types of lightweight, asymmetrical capacitor devices.
One cylindrical device that he built weighed between 3 and 6 grams and achieved maximum thrusts equal to as much as half of its weight.
1
For this design, he used a sheet of insulating plastic film that was a few mils thick and was wrapped around a cylinder 4.75 inches in diameter and 4.4 inches long (figure 12.1).
A 2.4-inch-wide aluminum-foil skirt was wrapped around the lower end of the cylinder, with a 0.5-inch overlap onto the plastic film, to serve as the negative electrode.
The positive electrode was an aluminum-foil tube measuring 0.25 inch in diameter and 3.6 inches in length that was located at the opposite end of the cylinder and positioned in line with the cylinder’s axis so that half the tube extended into the cylinder’s interior.
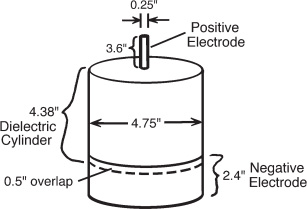
Figure 12.1.
A cylindrical-shaped ion-producing device built and tested by Tom Turman.
Its construction was based on reports of “lifter” tests carried out by Thomas Townsend Brown.
(Based on a sketch by Turman)
Turman found that lift increased exponentially with increasing voltage, V, approximately as V
2
to V
3
, confirming similar results found in Brown’s earlier work.
Turman’s cylinders developed thrusts ranging from 0.3 to 3.5 grams (5 to 50 grains) when energized with voltages ranging from 35 to 135 kilovolts with a current draw of a few milliamps.
He found that the amount of thrust depended on the type of insulating film he used in making the cylinder.
He obtained greater thrusts with materials having greater dielectric constants, observing thrust to increase according to K
2
to K
2.3
(figure 12.2).
He also found that thrust depended on the dimensions of the device, such as the length of the positive electrode and its depth of penetration into the cylinder, the length of the cylinder, and to some extent the width of the aluminum-foil skirt.
Data from thrust tests he conducted on a 13.75-inch-diameter cylinder are presented in table 1.
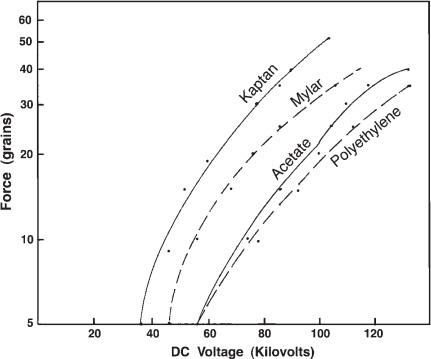
Figure 12.2.
Chart of lift produced by 4.75-inch-diameter cylindrical test
devices made from various types of plastic film with differing values of
dielectric constant (K).
Curves are shown for Kaptan (K = 3.7), Mylar
(K = 3.1), acetate film (K = 2.9), and high-density polyethylene (K = 2.3).
(After T.
Turman)
| TABLE 1. VARIATION OF THRUST WITH CHANGES IN LENGTH OF CYLINDER AND DEPTH OF POSITIVE ELECTRODE (Tested at 250 Kilovolts) | ||
| Length (inches) | Depth (inches) | Lift (grams) |
| 10.9 | 2.5 | 22 |
| 11.4 | 2.3 | 20 |
| 11.6 | 1.1 | 20 |
| 12.1 | 2.4 | 16 |
Turman obtained the greatest thrust when applying high-voltage DC pulses, an effect Brown also had noted.
When energized in a pulsed fashion, Turman’s device achieved thrusts nearly sufficient to self-levitate.
He found that his cylinder would also develop a thrust when energized with AC, but not as much as when energized with DC.
The unbalanced electrostatic force effect described in chapter 3 accounts for the thrust that would be developed when a reversed voltage polarity was applied to the cylinder.
Regardless of whether the smaller upper electrode had a positive or negative polarity, more ions would have been emitted in the vicinity of the small upper electrode, where the electric field density was greater, and this would have exerted a strong upward-repulsive force.
This force would have been greater than the downward-repulsive force component produced in the vicinity of the lower-cylindrical electrode, where fewer oppositely charged ions would have been generated and where the consequent repulsive force would primarily have been directed radially outward, away from the cylinder’s central axis.
Consequently, electrostatic ion-repulsion effects appear to dominate over electrogravitic effects in lightweight devices producing a nonlinear field.
The same applies to the lifter experiments carried out by later researchers.
Turman noted that his cylindrical thruster device was a copious producer of ion wind, and hence, he could not rule out ion wind as the principle mode of propulsion.
However, observing that the electric field between the two electrodes was highly nonlinear, he predicted that the device should exhibit a discernible Biefeld-Brown effect when tested in a vacuum environment.
He had almost finished building the vacuum equipment necessary to conduct these tests when he had to disassemble everything and move his residence due to a job change.
Afterward, he never reassembled his equipment.
Turman’s cylindrical device did not come close to giving the kind of vertical lift that Brown had obtained from his 100-gram, triarcuate-shaped disc (figure 3.2).
Nevertheless, Brown expressed considerable interest in the design.
In one of their telephone conversations, when Turman told Brown about getting really good thrust from his cylinder devices, Brown quizzed him extensively about them and said, “[M]ake some drawings and send me those drawings because I am really interested in those cylinders.”
Turman sent him some drawings and data, and subsequently, on November, 1, 1971, Brown wrote back, saying, “Your sketch shows a point and ring configuration of electrodes with an intermediate dielectric tube.
I take it the ends of this tube are open and the airflow is in the direction of the divergent field.
This would make the tube assembly move in the opposite direction, that is, toward the small positive electrode.
Is this not so?
.
.
.
Have you observed any thrust with the positive end of the tube closed?”
2
Another asymmetrical capacitor design that Turman tested consisted of a flat 8-inch-diameter disc of polyethylene film with aluminum-foil electrodes attached to its upper and lower surfaces.
3
The upper (positive) and lower (negative) electrodes consisted of a 1-inch-diameter foil disc and a 7-inch-diameter foil ring (see figure 12.3).
The disc was supported by a balsa-wood structure attached by monofilament lines to an equal arm balance for weight measurement.
The device was found to develop a lift of up to 30 percent of its weight when energized.
As with the cylindrical device, this flat disc also developed lift when AC was applied to it, but not as much as with DC voltage.
Also, the device was found to perform better with DC pulses than with steady DC.

Figure 12.3.
A flat-profile electric disc designed and tested
by Tom Turman.
(Based on a sketch made by T.
Turman)
Turman also attempted to duplicate Brown’s flying-disc device.
He made a 28-inch-diameter saucer out of cardboard and covered it with aluminum foil (figure 12.4).
4
The disc was 2.5 inches thick at its center and tapered to 0.12-inch-diameter blunt edge at its periphery.
He curved a 125-mil-diameter brass rod 70 degrees around the disc to serve as the outboard positively charged electrode and spaced it 4.75 inches from the negatively charged disc with a series of Plexiglas insulators.
In a static test, the device developed only 4.5 grams of thrust when energized to 80 kilovolts.
This yielded a thrust-to-weight ratio of only 1 percent, far lower than even the thrusts observed in the 1952 Office of Naval Research tests in which Brown’s discs developed thrusts of 18 grams under a charge of 47 kilovolts.
Because of this disappointing performance, Turman wrote to Brown inquiring what might be wrong with the basic design he had used.
In his November 1, 1971, letter (see
appendix A
), Brown responded by drawing a picture of his electric disc (shown in figure 2.6).
This indicated that Brown used a much smaller-gauge wire as his positive electrode, one that had a diameter of 1 mil (0.001 inch).
In his electrokinetic apparatus patent, Brown noted that small-diameter wires should be used for discs energized with voltages less than 125 kilovolts.
For discs energized at higher voltages, he recommended that the positive electrode consist of a hollow pipe or rod having a diameter of 0.25 to 0.50 inch.
Turman, however, tested his discs in the lower-voltage range with a wire that was more than one hundred times larger in diameter than Brown would have used.
This may explain why Turman got lower thrust from his disc.
Also, the radius of curvature of the edge of the triarcuate disc in Brown’s drawing was eight times larger than in Tom’s design (0.50 inch rather than 0.06 inch).
In designing his disc, Turman had originally been guided by the diagram Brown gave in his 1960 electrokinetic apparatus patent.
