Secrets of Antigravity Propulsion (17 page)

According to subquantum kinetics, force action is fundamentally a reaction-kinetic process rather than a mechanical process, one in which the particle’s core field readjusts its concentration pattern in response to the disequilibrium caused by an imposed field gradient.
Thus the field’s induction of force and acceleration is accomplished with no recoil force being applied back on the field.
No momentum transfer is involved.
Similarly, the potential gradient generated by a charge or mass becomes established in the ether and is able to operate on charges and masses without any deference to the charges or masses that originally generated it.
Thus, in subquantum kinetics it is perfectly acceptable for a field to accelerate the very same charges that generate it.
This field autonomy is key to understanding how unbalanced electrostatic forces can induce motion in an asymmetrical capacitor, a subject we examined in the previous chapter.
French inventor Jean-Claude Lafforgue proposes a similar idea in his 1991 patent on an asymmetrical thrust capacitor.
He suggests that when a capacitor is charged, the fields it generates have their seat in the local space-time continuum reference frame, allowing them to act on the capacitor without any reaction force being directed back to the capacitor itself.
Thus, he suggests that the electric fields generated by a properly shaped asymmetrical capacitor can exert unbalanced electrostatic forces on the capacitor, whose residual is capable of displacing the capacitor relative to its initial rest frame.
In his patent Lafforgue states:
It is acceptable then to consider that
F
[electrostatic force] rests its support on
E
[electric force field intensity], that is to say, on the space-time continuum .
.
.
It is the same for all the electrodes whatever their orientation and polarization .
.
.
Whether the electrodes are at rest or in motion does not at all change the values of
ρ, of σ, of q, of
E,
nor of
F
.
So under the action of the “force of expansion,” the isolated system moves and drags with itself σ and
E
and consequently
F
.
Our isolated systems are therefore self-accelerated.
15
Lafforgue’s term “force of expansion” refers to electrostatic pressure, that is, the electrostatic force
F
= σ
E
present on a portion of the capacitor plate divided by the surface area it acts through.
Lafforgue does not refer to the notion of an ether.
He uses instead the relativistic term “space-time continuum,” and he adopts the convention of working with force field intensity,
E
, rather than the electric potential gradient
∇
φ
E
.
However, his conclusions about a capacitor’s self-field action, which are based on experimental observation, are surprisingly identical to those predicted by subquantum kinetics.
Hence, his work may be considered as independent support for the subquantum kinetics approach.
Tests performed on one of Lafforgue’s asymmetrical capacitors are discussed in chapter 12.
Classical physics assumes that subatomic particles produce only matter-attracting gravitational forces regardless of their charge polarity.
Classical theory doesn’t describe what a gravitational field is or how it exerts its force; it just identifies it and mathematically represents how gravitational force is related to the mass of a body and to an observer’s distance from the body.
As for antimatter, there are a variety of opinions among physicists.
Some believe that antimatter particles should produce matter-attracting fields and others believe that they should produce matter-repelling fields.
General relativity, like classical physics, also asserts that all subatomic particles should produce attractive gravity fields regardless of their electric charge.
Yet it also advances the additional proposition that these gravitational effects come about because the body’s mass warps the surrounding metric of space and time and as a result induces an attractive motion in neighboring masses.
Relativity does not state how matter manages to accomplish this warping feat; it simply states this as a given.
Although fancy equations are presented to describe the warping assumption, they do not themselves provide any insight as to why matter, a physical quantity, might affect the geometry of space or the rate at which time passes.
The initiate is asked to accept this on faith.
Subquantum kinetics, on the other hand, does explain how a material body generates its electric and gravity potential fields, why these two fields are interlinked, and also how these fields induce forces on charges and masses.
Furthermore, it describes how a material particle comes into being in space, another point on which conventional physics is a bit vague.
Most physicists are reluctant to consider ether-theory explanations of particles and fields because relativists have long drummed into them the misconception that the idea of an ether, with its preferred reference frame, has been disproved.
Usually, they cite the Michelson-Morley experiment’s failure to detect a directional variation in the velocity of light.
However, many have argued that the experiment’s null result was due to the fact that it was conducted underground, where the ether was stationary in the reference frame of the rotating Earth.
Other experiments carried out by Georges Sagnac, Dayton Miller, and Ernest Silvertooth have since shown that the one-way velocity of light is not a constant.
16,
17,
18,
19,
20
Hence, the results favor the notion of an ether over relativity’s relative-frame notion.
The vindication of the ether-frame concept even impacts us every day in a practical sense.
To establish proper synchronization of the clocks in the global positioning system satellite array, computer software must make allowances for the change in radio signal velocity caused by the array’s geosynchronous rotation relative to the local ether frame.
Were this not done and the network was instead synchronized in accordance with the pronouncements of special relativity, a hiker would be unable to accurately establish his latitude and longitude coordinates.
The military knows this quite well.
Moreover, general relativity has no exclusive claim over tests carried out to check its predictions, such as the gravitational bending of starlight by the Sun and the precession of Mercury’s orbit.
All of these have also been accounted for in terms of classical physics effects.
21
It might be added that these same gravitational effects are also predicted by subquantum kinetics.
What general relativity refers to as a spatial warping of starlight photons by a celestial mass subquantum kinetics understands to be a refraction of photons (ether waves) by the body’s gravity potential gradient (G-on concentration gradient).
The gravitational time dilation phenomenon that all massive bodies experience and that relativity interprets again as an inexplicable warping of space is understood as a clock retardation effect that arises as a result of the reduction of the G-on concentration within the star or planet (as G decreases, so too does X, and in turn so too does the X-Y flux rate that is responsible for all physical action).
The gravitational redshift of light emitted from a massive celestial body occurs for a similar reason.
Subquantum kinetics also accounts for special relativistic effects.
All of these effects emerge from the five basic equations diagrammed in figure 4.1 (see page 118).
In summary, special and general relativistic effects emerge as corollaries of subquantum kinetics, but without requiring the magical warping of space-time.
So it is not surprising that highly classified black-budget programs embrace the concept of an ether in their attempts to understand the gravity-defying technologies that they have been developing.
They have no obligation to please the academic physics establishment, which still teaches the rocket principle as the ultimate in space propulsion technology.
Norwegian researcher Dr.
Björn Overbye points out that most physicists find it virtually impossible to visualize and understand relativity theory because it requires that one think in terms of four dimensions.
He says, “Even experienced mathematicians and theoretical physicists who have worked with higher dimensional space for years admit that they cannot visualize them!
Instead, they retreat into the world of mathematical equations.”
22
According to the Nobel laureate Hannes Alfvén, “The people were told that only Einstein and a few geniuses that were able to think in four dimensions could understand the true nature of the physical world.
Science was something to believe in, not something that should be understood.”
23
Subquantum kinetics, on the other hand, offers us a path back to visualization and understanding.
It is based on a simple conceptual framework, but to follow it one must forget the misleading models that have been taught in the past, quantum mechanics and relativity theory being among them.
Since the theory is not easily presented in the space of a few paragraphs, the reader is referred for more details to the journal articles cited at the beginning of this chapter and to my book
Subquantum Kinetics
, all of which deal more thoroughly with the subject.
24
The more philosophically inclined are referred to my book
Genesis of the Cosmos
, which presents a less technical introduction to the subject.
25
4.2 • VIRTUAL CHARGE ELECTROGRAVITIC EFFECTS
In earlier writings of how subquantum kinetics predicts an electrogravitic connection, I did not also consider that virtual-charge gradients might also produce electrogravitic effects.
However, it is reasonable to expect that, like real charges, virtual charges also should induce gravity potentials.
Moreover, gravitational thrusts on a capacitor dielectric arising from virtual charges may in some cases be far greater than those produced by the real charges creating the capacitor’s electric field.
So it is evident that the scope of the subquantum kinetics electrogravitics prediction should be expanded to include such virtual-charge effects.
Let us proceed to derive this by considering a charged asymmetrical capacitor that establishes a nonlinear electric field across its dielectric.
Due to the math involved, the material presented in the next several pages may be a bit challenging for those who have not had a course in college physics.
Some, then, may want to skip over it.
But those wishing to acquire a nuts-and-bolts understanding of how antigravity technology might work are encouraged to read this section, if not now, at least at some later time, for this material is referenced frequently later in the book.
As was explained above, subquantum kinetics identifies an electric potential gradient with an X-on or Y-on ether concentration gradient.
Consider a charged asymmetrical capacitor whose negative plate is smaller than its positive plate.
With such a field geometry, the voltage gradient will vary nonlinearly with distance across the dielectric, the field gradient getting steeper toward the capacitor’s smaller negative plate.
Represented in terms of the X-on etheron concentration component, C
x
, X-on concentration will rise nonlinearly, reaching a maximum at the negative plate.
X-ons will continuously diffuse down this concentration gradient away from the negative plate, their flux per unit surface area being represented by the symbol
Ф
x
, called the X diffusive flux vector.
It is related to the X-on concentration gradient,
∇
C
x
, by the formula
Ф
x
(r) = –D
x
∇
C
x
(r), where D
x
is the diffusion coefficient.
Suppose that we consider three adjacent volumes in the capacitor dielectric aligned along the axis of the capacitor and located near the capacitor’s negative plate (see lower three boxes in figure 4.4).
Because the field potential varies nonlinearly with distance across the dielectric, the X-on concentration gradient,
∇
C
x
, between box 1 and box 2 will be steeper than that between box 2 and box 3.
Therefore, more X-ons will be induced to flow into box 2 than will be induced to leave from box 2.
As a result of this flux imbalance, the number of X-ons in that box will increase at the rate
Ф
x(in)
– Ф
x(out)
.
This has the effect of raising the X-on concentration in that box, which is equivalent to lowering its electric potential, negative potential being correlated with increased X-on concentration.
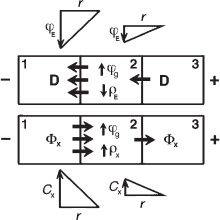
Figure 4.4.
The flux vector divergence concept.
The lower boxes show adjacent volumes of space along the polarization axis of a capacitor with their corresponding X diffusive flux vectors, Ф
x
, arising from a prevailing nonlinear X-on concentration gradient.
The upper boxes show, as in conventional theory, the corresponding electric flux density vectors,
D
, arising from a prevailing electric potential gradient.
(P.
LaViolette, © 2007)
Because there is a net inflow of X-ons into box 2, the divergence of the X diffusive flux vector
∇
•Ф
x
for that box will be a negative quantity.
This diffusive-flux-vector divergence by definition is calculated from the variation of X-on concentration C
x
(r) using the equation
∇
•Ф
x
(r) = –D
x
∇
2
C
x
(r).
This negative Ф
x
divergence, in turn, is equal to a quantity called the X production rate balance
density, ρ
x
, a scalar quantity that represents the rate, Q
x
, at which X-ons enter a unit volume dV.
This is mathematically expressed as
ρ
x
(r) = Q
x
(r)/dV = –
∇
•Ф
x
(r) = –D
x
∇
2
C
x
(r).
The X production balance density, ρ
x
, is the ether counterpart of
the negative virtual electric charge density, –ρ
E
.
*12
Thus the excess influx of X per unit time into box 2 would act as though a negative electric charge density, –ρ
E
, was present in that box.
Also, the X diffusive flux vector, Ф
x
, is the ether equivalent of the electric flux density vector,
D
, of conventional theory.
Physicists also refer to
D
as the electric displacement, but we use here the flux density vector designation since it more closely approximates the terminology used for its ether counterpart.
It should be mentioned that all of these conventional physics terms were originally developed in the context of 18th-and 19th-century ether models.
The upper set of boxes in figure 4.4 illustrates how these etheron fluxes would be expressed in conventional physics terms using
D
and ρ
E
.
A nonlinear electric potential gradient
∇
φ
E
is assumed to extend across the capacitor dielectric with the potential gradient steepening toward the negative electrode on the left.
This field gradient induces a greater electric flux density to flow out from box 2 (to the left) than to flow into box 2 (from the right).
Consequently,
D
has a positive divergence, which by definition creates a negative virtual-charge density in that box.
In conventional terminology, this is expressed as
∇
•
D
(r) = –ε
∇
2
φ
E
(r) = –ρ
E
.
Rearranging these terms we may write:
(6)
ρ
E
(r) = –
∇
•
D
(r) = –ε
∇
•
E
(r) = ε
∇
2
φ
E
(r)
Here we also include in the expression the term –ε
∇
•
E
(r), which expresses this equivalence in terms of the permittivity times the divergence of the electric field intensity,
E
, for those who are familiar with this alternate term.
However, in the case of real negative charges such as electrons, the
D
vectors would instead be inward directed making the divergence term
∇
•
D
a negative quantity.
If this subtle difference between real and virtual charges is not appreciated, one might mistakenly assign an incorrect polarity to virtual charges and calculate gravity thrust vectors pointing in the opposite direction.
Taking the etheron model as an example, if real negative charges were present in box-2, X-ons would be entering the box through X-on creation attributable to the Model G reactions.
The resulting X-on surplus would produce an outward diverging flux, making the divergence term
∇
•Ф
x
a positive quantity.
In the case of a negative virtual-charge density, on the other hand, the X influx arises from the spatial redistribution of X-ons, which enter the unit volume as a result of the electric field’s nonlinearity.
Thus the diffusive flux vectors will instead point inward, making the divergence term
∇
•Ф
x
a negative quantity.
Based on equation 6 above, we conclude that virtual charge is formed wherever the field’s electric flux density vector
D
acquires a nonzero divergence value, div
D ≠
0, or in other words, wherever the derivative of
D
differs from zero.
Expressed in terms of the electric potential field, φ
E
(r), a virtual charge would arise wherever the second derivative of the field’s electric potential becomes nonzero, that is,
∇
2
φ
E
≠ 0.
For the second derivative to be nonzero, the magnitude of the field’s electric potential must vary nonlinearly with distance.
Now, going back to our ether flux model, let us consider how these virtual electric charge densities would produce a gravitational field across the capacitor.
The positive X production rate balance density in box 2 (lower half of figure 4.4) results in the creation of a positive G production rate balance in that box due to the reverse reaction, G ← X, which in turn produces a local increase in G-on concentration, C
g
.
With this surplus G production rate, the volume acts as though it contains a negative virtual mass density that produces a local increase in gravity potential, φ
g
.
Consequently, a negative divergence of the X diffusive flux vector leads to an increase in gravity potential at that point.
Thus subquantum kinetics leads to a charge-mass equivalence similar to that stated in relation 2 of chapter 1, except here we broaden the definition of charge density so that we consider the electrogravitic effects of a virtual-charge-density gradient opposed to a real-chargedensity gradient.
Hence we may state that a virtual-charge density of magnitude ρ
E
creates a proportional virtual mass density of magnitude ρ
m
, that is, ρ
m
∝
ρ
E
.
If the negative virtual-charge density varies with distance across the capacitor’s dielectric, then there will be a corresponding variation in negative virtual mass density and a gravity potential gradient will form across the dielectric.
Given that this virtual mass density creates a proportional negative gravity potential field, ρ
m
∝
–φ
g
(r), we conclude that the gravity potential at a given point r should be proportional to the negative charge density at that location.
By using equation 6 above, this may be mathematically expressed as:
