Pythagorus (43 page)

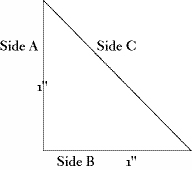
First, review the problem. The Pythagorean theorem says that the square of Side A plus the square of Side B will equal the square of Side C. Say that Side A measures 1inch. Side B also measures 1inch. The square of 1 is 1. So the square of Side A plus the square of Side B (1+1) equals 2. If the Pythagorean theorem is correct, the square of Side C must likewise be 2, but what is the
length
of Side C? You cannot find out if you cannot calculate the square root of 2. Here is how Russell suggested the Pythagoreans might have approximated it:

Make two columns: Column A and B, and let each begin with the number 1.

To get the next pair of numbers:

For Column A, add the first A and B (1+1).

For Column B, double the first A and add the first B (2+1)

Continue using the same method of getting the next pair of numbers, always using the two previous numbers as your ‘former A and B', and you soon have:

For each pair the following is true: 2A squared minus B squared equals either 1 or minus 1. In each case, B divided by A is close to the square root of 2, and the farther down the chart you move, the closer it is to the square root of 2, though it never quite gets there because the square root of 2 is not a rational number. Would this have satisfied the Pythagoreans? One cannot help thinking that for people who believed they had found complete rationality and simplicity in the universe, it would have been poor consolation.

Russell in great part credited Pythagoras with linking philosophy with geometry and mathematics, with the result that geometry and mathematics had been an influence on philosophy and theology ever since – an influence Russell regarded as ‘both profound and unfortunate'. In geometry, as Euclid and other Greeks established it, and as it is still taught today, one does not begin in a void, thinking nothing true unless proved. There are statements that are not proved but are ‘self-evident' (or at least seem to be), called axioms. Some bit of self-evident truth must be there as the starting place. That may seem a shaky foundation to build on, but many generations have managed to accept it and proceed. Beginning with the axioms, the next step is to use deductive reasoning to arrive at things that may not be at all self-evident, called theorems. Axioms and theorems are supposed to be true about actual space; they are something that could be experienced. In other words, by taking something self-evident and using deductive thinking it is possible to discover things that are true of the actual world.

Russell had no argument with this line of thinking in geometry. His regret was that it been applied to other areas. The American Declaration of Independence, for example, declared, ‘We hold these truths to be self-evident', on the assumption that there are, indeed, things having nothing to do with geometry or mathematics that are so clearly true that no sane person would question them. The words ‘self-evident' were one of Benjamin Franklin's changes in the draft of the Declaration. Thomas Jefferson had written, ‘We hold these truths to be sacred and undeniable', a less down-to-earth version of the same idea. The point was that everyone could proceed from there without looking back. But could they?

Russell was not really trying to undermine Franklin, but he was disgruntled that the process by which geometry is done had been co-opted not only by brilliant rebels but by theologians. Thomas Aquinas had used it in arguments for the existence of God. His arguments did not start from nothing, but rather from ‘first principles'. In fact, what Aquinas meant by ‘science' was a body of knowledge that has ‘first principles' or ‘givens'. Again, Russell blamed the Pythagoreans: ‘Personal religion is derived from ecstasy, theology from mathematics; and both are to be found in Pythagoras.' The Pythagorean marriage of mathematics and theology had polluted the religious philosophy of Greece, then the Middle Ages, and so on through Immanuel Kant and beyond. In his essay ‘How to Read and Understand History', Russell lamented,

There was a serpent in the philosophic paradise, and his name was Pythagoras. From Pythagoras this outlook descended to Plato, from Plato to Christian theologians, from them, in a new form, to Rousseau and the romantics and the myriad purveyors of nonsense who flourish wherever men and women are tired of the truth.
5

Russell identified some characteristics of what he saw as a blending of religion and reasoning, of ‘moral aspiration with logical admiration of what is timeless', in Plato, Augustine, Thomas Aquinas, Descartes, Spinoza, and Kant. Their offences were belief in insight or intuition as a valid route to knowledge, a route distinct from analytic intellectual processes; denial of the reality of time and the passage of time in the ultimate scheme of things; belief in a unity of all things and a resistance to any fragmentation of our knowledge of the world. This ‘philosophical mysticism' – a term used not by Russell but coined by the physicist John Barrow – according to Russell ‘distinguished the intellectualised theology of Europe from the more straightforward mysticism of Asia.'
6
However, he believed it was a much earlier form of Eastern mysticism that had entered, through Orphism, into Pythagoreanism, in which fertile ground it had taken root to develop into the intellectualised but still partly mystical theology of Europe.

Russell was not a lone voice. He was one of the founders of a school of thought called logical analysis, an effort ‘to eliminate Pythagoreanism from the principles of mathematics', ridding it of ‘mysticism' and ‘metaphysical muddles'. He and those who joined him in this movement refused to indulge in what they saw as ‘falsification of logic to make mathematics appear mystical, and the practice of passing off, as authentic intuitions of reality, prejudices about what is real'. Russell also tried to put logic to work in an attempt to clarify issues in philosophy, making ‘logical analysis the main business of philosophy', rejecting any notion that moral considerations have a place in philosophy or that philosophy might either prove or disprove the truth of religious doctrine. Philosophy, stripped of its ‘dogmatic pretensions', would nevertheless ‘not cease to suggest and inspire a way of life'.

While Russell and his colleagues recognised there were questions they could not answer, they preferred to leave them unanswered rather than cling to what they felt were foolish and misleading ‘answers', or believe there are ‘higher' sources of answers:

The pursuit of truth, when it is profound and genuine, requires also a kind of humility which has some affinity to submission to the will of God. The universe is what it is, not what I choose that it should be. Towards facts, submission is the only rational attitude, but in the realm of ideals there is nothing to which to submit.
7

Reading that, one cannot avoid the conclusion that Russell was far more ambivalent about the issue of ‘discovery' versus ‘invention' than he was willing to admit.

Though he deplored the way mathematics had been ‘misused' in other areas, Russell believed that what he was insisting philosophy do – utilise logical analysis, adopt methods of science, and try to base its conclusions on impersonal, disinterested observations and inferences – should be applied in all spheres of human activity. This would bring about a decrease of fanaticism and an increase in sympathy and mutual understanding. He attempted, with scant success, to apply logical analysis to fields such as metaphysics, epistemology, ethics, and political theory, making (ironically) what was arguably a ‘Pythagorean' leap of faith that what seemed to be a good idea in one area of experience would be a good idea in all.

Russell decried yet another aspect of the Pythagorean legacy: The Pythagoreans lived by an ethic that held the contemplative life in high esteem and had bequeathed to the future something he called ‘the contemplative ideal'. In the fable about the people at the Olympic Games, Pythagoras and his followers were in the third group, those who had come to watch. These ‘onlookers' celebrated not practical but ‘disinterested' science – in other words, they were disengaged from the world of buying, selling, and competing, able to view the whole scene with greater objectivity – thinking that their roles as independent observers placed them in a better position on the path of escape from the eternal circle of the transmigration of souls. Russell contrasted this view with a modern set of values that sees the players on the field as superior to mere spectators, and that admires politicians, financiers, and those who govern the state, the ‘competitors in the game', above those who keep to the sidelines and watch and make wise observations.

Nevertheless, said Russell, the elevated status of the ‘gentlemanly on-looker' who does not dirty his hands has endured, and this began in ancient Croton, was carried forward with the Greek idea of genius, then with the monks and scholars of the church, and later with the academic university life. He criticised all these, including ‘saints and sages', who, except for a few activists, had lived on ‘slave labour', ‘or at any rate upon the labour of men whose inferiority is unquestioned'. It is these ‘gentlemen', these ‘spectators at the Games', he lamented, who have given us pure mathematics, and that contribution has meant, for them, prestige and success in theology, ethics, and philosophy, because pure mathematics is generally regarded as a ‘useful activity'. Russell did not mention that he himself was one of these gentlemen he was criticising – literally so, for he was born into the British nobility, studied at the University of Cambridge and became a fellow of Trinity College there, and spent most of his life as an academic and writer. However, he did, certainly, become one of the activists as well.

Parodoxically, Russell believed passionately in some ideals that he could not have arrived at by confining himself to strict empiricism, deductive thinking, and the scientific method. Perhaps his intuitions about what is right and what is wrong were, indeed, self-evident. To judge from his writings, these ideals became for him a higher priority than his logical analysis. He was a pacifist during World War I, and this unpopular stand cost him his Cambridge fellowship and landed him in prison for a while, but in 1939, in the face of the Nazi threat, he renounced pacifism. He was a lifelong, outspoken opponent of Nazism, Soviet communism, and belief in God. He campaigned vigorously for nuclear disarmament and against the Vietnam War. In these causes he was superbly able to write essays for popular readers that often seemed to begin as polemics but ended with reasoned arguments.

Russell was an impassioned and influential man, who recognised that there was a directionality built into human beings that makes us at least seem to be existing somewhere on a continuum from evil to good, ugliness to beauty, unfairness to justice, mediocrity to greatness, weakness to strength, with the ultimate in every case being off the scale, over the horizon of human comprehension or imagination. In his espousal of a mathematical philosophy that would soon be outdated, but still more in the positions he took against nuclear weapons, war, and what he saw as cruel dogmatisms, Russell, paradoxically, lived by this Platonic, perhaps Pythagorean-based view of the world. Ironically, it was the decisions he made on that foundation that ultimately made him memorable.

Arthur Koestler's picture
of Pythagoras was far more positive. Born in Budapest in 1905, Koestler was an author and journalist and probably the most widely read political novelist in the world in the 1940s and early 1950s. His writing highlighted the moral dilemmas caused by the rise of communism and the two world wars. Koestler, like Russell, spent time in prison. While serving as a foreign correspondent in Spain, he was captured by Franco's troops and sentenced to death. The British government intervened and Koestler was able to return to London. As he aged, he took an increasing interest in science and the history of ideas and knowledge. His 1959
The Sleepwalkers
was a masterpiece when it came to splendid writing and an ability to convey Koestler's passion for science, scientists, and scientific ideas. It was the first in a trilogy that continued in 1964 with
The Act of Creation
and in 1967 with
The Ghost in the Machine
. Koestler died in 1983. He was suffering from leukaemia and Parkinson's disease, and he and his wife, both advocates of voluntary euthanasia, together took their own lives.