Our Cosmic Ancestors (25 page)

The Tiahuanaco foot, as calculated from the dimensions of the temple, does not correspond exactly to the local foot as I calculated it from the geographic coordinates. But the difference is only 6/10 of mm, and it could be caused by no less than four different reasons. First, it could be that our ancestors did a poor calculation, which seems to be out of the question, judging by all of the other calculations that they made routinely and exactly. The second reason might be the altitude or the irregularity of the local formation of the Earth's crust, which seems to bulge, giving a longer degree at Tiahuanaco than at sea level. This deformation must have been even greater when the big moon caused the belt around the equator. The third possibility is that Tiahuanaco was part of a large empire, and the local degree was taken from a centre 42 km farther north, from a latitude of 16
^°
04' south. It would be really curious to find prehistoric ruins at the latter latitude some day. The fourth and most believable explanation is that since Tiahuanaco was built and its calendar calculated, the equator has moved north by 23 minutes of arc.

No matter what the explanation, the foot of Tiahuanaco of 0.297234 m must be the correct value. Bellamy and Allen themselves estimated the Tiahuanaco cubit at 0.4458 m, which gives a foot of 0.2972 m. Another proof that these values are correct is the weight that can be derived from the Tiahuanaco cubic foot - 26,260 g, which is exactly the weight of one talent of gold or silver used for thousands of years throughout the Mediterranean basin. Does that prove that trade existed between these ancient cultures, or is it just proof that both cultures had common roots? Moreover, if we measure with that cubit the dimensions of the different buildings, we always find numbers of cubits that are divisible by 7, 9,11, 12, and 13, and allow us to calculate important astronomical and mathematical ratios such as 22/7, 14/11, or 12/11, which we have already mentioned.

Now that we know the exact dimensions of the cubit, the foot, and the finger, it is interesting to go back to the andesite pillars of the western gallery and try to find out what the dimensions there tell us. Here are nine dimensions, all in cubits, that can simultaneously explain the irregularity of the spaces between pillars and prove that at the time these pillars were set, there was in the sky a moon much larger and much closer than our present one. Since, of the eleven pillars, the outer two are there only to frame the field of vision, let's look at the nine possible combinations of the nine spaces between the inner pillars and each time add the pillars’ own width to the distance. Thus we obtain the following measurements in cubits: 201/4, 19, 19, 18, 181/4, 171/4, 191/4, 17 3/4, 191/4.

We now have seven different intervals, two of them repeated twice, probably to measure something very big, like a moon so close to the Earth that it would vary in its apparent diameter because of the elliptic path it was describing in the sky. But it does not take long to discover that, if an observer places himself 162 cubits from the pillars, the angles from there represented by the above intervals read, starting from the south: 7
^°
, 6
^°
40', 6
^°
40', 6
^°
20', 6
^°
30', 6
^°
, 6
^°
50', 6
^u
10', and 6
^°
50', giving a total for the observation field of 59
^°
. The average apparent diameter of the moon at that time must have been 6 1/2 , or 11.68 percent bigger than the diameter that we calculated from the laws of celestial mechanics for our present Moon, npr
^-
,iy, 5.82
^°
. We can conclude that the moon of that period was 12 percent larger than the present one.

We have yet to talk about an additional problem tied in with the theory of the four moons, the age of Tiahuanaco. One way to estimate its age would be to use the climatic cycle of 21,000 years that we discussed when we talked about ice ages in
The Constant of Nineveh.
This cycle is the time period needed for the date of the equinox to arrive at the same moment when the Sun is at its perigee - the point closest to Earth. If we want to believe the Tiahuanaco calendar, this timetable was calculated on a date when the spring equinox in the southern hemisphere coincided with the Sun in perigee, a situation that last occurred 6,000 years ago and, before then, 27,000 years ago.

Now, the Tiahuanaco calendar could not possibly have been calculated only 6,000 years ago. The ruins are obviously much older than that, and also, all of the legends from 4,000 BC tell us that our present Moon was already there, shining bright and silvery. So we must believe that the true age of the Tiahuanaco calendar is about 27,000 years, about the same as the cave paintings of Lascaux and Altamira. What is even more surprising is the fact that the numbers 264 and 288 were used by other ancient civilizations in South America, and that the phenomenon of the big moon was known throughout Central America.

in the region of Cuenca, in Ecuador, Juan Moricz found buried caves in 1965 that until then had been known only to the local Indians. His information is scant and inaccessible, but the discoverer reported that the central hall of treasures of these caves has dimensions of 137.7 by 150.2 m, proportional to 264 and 288, numbers that I found
and that were not known to anybody until my first book was published. Another surprise is that these two dimensions of the hall of treasures in the Cuenca caves correspond exactly to the local foot of 0.3476 m and the cubit derived from it of 0.5214 m. These dimensions are real and we will find them later. They also give us the precise length of one degree of longitude at 2 1/2
^°
south latitude, which is nearly the latitude of Cuenca.

Father Crespi, who died recently, used to run the local gold museum in Cuenca. He had been a lifelong friend of the local Indians and custodian of the treasures that were brought to him by his Indian friends when they needed something. Most of the objects in the Cuenca museum are pure gold and of extraordinary beauty. The masterpiece is a golden plate 52 cm long, 14 wide, and 4 thick with 56 hieroglyphs. Next to it is a weeping god, also solid gold, 52 cm high, which happens to be the length of the local cubit.
And the god's hands and feet have only four fingers, like the god of Tiahuanaco.

Strange coincidences? A cubit of longitude, the hall in the caves, the gold tablet, and the gold idol with four fingers; that makes four times the same measurement appears, which we will call the Cuenca cubit of 0.5214 m. When we divide it by 28, we obtain one finger of 18.62 mm. The gold plate of the Cuenca museum keeps surprising me. At first it seemed to be only a standard of length. Then it looked also like a unit of volume of 28 x 2 x 7.5 fingers, or 420 cubic fingers. Finally, with a specific gravity of 19.37 for the very pure Inca gold, it certainly was a unit of weight of 52,520 grams, or two gold talents from the Mediterranean. Now, call
that
a coincidence!

So far none of the fifty-six hieroglyphs has been deciphered. It could be an alphabet of fifty-six letters. It could be a lunar calendar of fifty-six years. It could be anything else. We simply do not know.
But these discoveries have already told us that the civilizations of Tiahuanaco and Cuenca had more than just the four-fingered gods in common.
And we also find the same basic numbers in Monte Alban and Teotihuacan, in Mexico.

The sunken court in Monte Alban measures 78.50 by 85.60 m, or exactly 264 by 288 Tiahuanaco ft, even though the two sites are separated by thousands of kilometres. Even more surprising are the pyramids of Teotihuacan whose dimensions again seem to be based on the two sacred numbers. However, the measurements at
Teotihuacan are a very controversial issue. I have three recent books on the subject all giving different numbers. Only one thing seems almost certain. if we divide 2,400 m, the length of the Grand Avenue, by the Teotihuacan yard of 1.0582 m, we obtain the Nineveh constant of 2.268. Is that another coincidence?

In short, we have convincing evidence that four separate American civilizations used the same numbers and the same units of measurement to express the two sacred numbers of astronomy that had the greatest importance for them, the numbers of days In the lunar and In the solar year at that time.

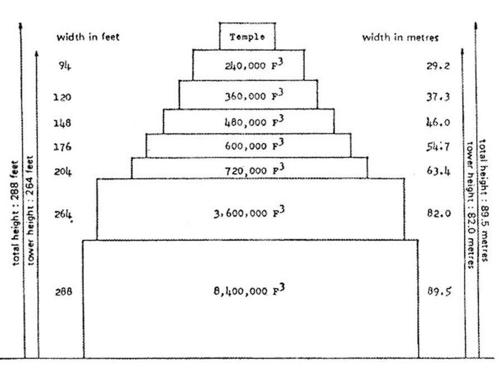The Tower of Babel
Original dimensions in metres and in Sumerian feet of 310.723 mm

This drawing shows the original dimensions of the Tower of Babel in metres and in Sumerian feet of 0.310723 metres. The tower was built with 57.6 million bricks and its volume of 14,400.000 cubic feet, or 432,000 cubic metres, was of the volume of the Great Pyramid of Cheops. In Babylon, 432,000 was also the length in years of the Great Year, and the ratio of 264 :288 was the same as the one used at Kalasasaya in Tiahuanaco.

There is another mysterious example of the use of the same sacred numbers on the other side of the world, namely, at the famed Tower of Babel. It was constructed in units of the Sumerian foot of 0.310723 m, out of 57.6 million clay bricks, each with a volume of 0.25 cu. ft. The volume of the whole tower was 14.4 million cu. ft, or 432,000 cu. m, six times smaller than the Cheops pyramid. The tower was 264 ft. tall, and on its top stood the 24 ft. high Temple of Marduk, making the total height of the tower 288 ft. The statue of Marduk was cast in solid gold and weighed 800 Sumerian talents, or 24 metric tons.

The Ziggurat of Ur
Original dimensions in metres and in Sumerian feet of 0.310723 mm This drawing shows the original dimensions of the Ziggurat of Ur. in metres and in Sumerian feet of 0.310723 metres. It was built with 9.6 million bricks and its volume was 2.4 million cubic feet, or 72.000 cubic metres, which represented of the volume of the Tower of Babel, or 5
¹
6 of that of the Great Pyramid of Cheops. The first tier has a 132 :144 ratio equal to 264 :288.

It really seems that the Tower of Babel was built with the Tiahuanaco proportion of 264/288 because not only its measurements in height but also the proportion of the two first terraces is such. Its total volume of 432,000 cu m ties it in with the metric system and with the number of 432,000 years, which is used even today by the descendants of the ancient Hindus as an astronomical and religious time cycle. The Babylonians used the same cycle, but divided it by 40, creating the time cycle of 10.800 years, which is found in many cultures. As for the Ziggurat of Ur, its volume was 1/6 of the Tower of It Babel, or 1/36 of the Great Pyramid of Cheops. Also, the surface of its first terrace was 2,268 sq. m!

We must recognize here, whether we like it or not, that widely separated cultures used similar systems for measuring length, volume, weight, and time, standards whose original sources have disappeared without recognizable trace. Yet the common heritage seems incontestable; and if we want to believe the Egyptian, Tibetan, and many other legends, the common source of all culture was a great island in the middle of the Atlantic Ocean that disappeared in the waves 12,000 years ago, the fabled Atlantis, which we will discuss next.