Mathematics and the Real World (31 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Cardano also suffered from shortage of money, and he tried to get it via games of chance and gambling, and for that purpose he developed mathematical methods of calculating what is today referred to as the relative frequency of numbers coming up in throws of dice, for example, as we mentioned above, calculating the number of times a pair of sixes would be thrown or how often the sum of the two upper faces would exceed ten. Cardano gathered these methods and other studies related to gambling into notes for a book, but it was not published until after his death. Cardano's and his contemporaries’ methods were limited to methods of calculation; in other words, they translated intuition into arithmetic without any logical mathematical basis. This changed very soon.
37. PASCAL AND FERMAT
The laying of the mathematical foundation of the theory of probability is generally attributed to correspondence in 1654 between two of the most famous mathematicians of their time, Blaise Pascal (1623–1662) and Pierre de Fermat (1601–1665). That claim contains an element of exaggeration, but, as we will see, that correspondence over several months, followed by the publication of an argument eventually known as Pascal's wager, did indeed provide the basic conceptual cornerstone of the theory of probability.
It was Pascal who initiated the correspondence when he asked Fermat for his reaction to his proposed mathematical solution to a question related to gambling. Pascal was shown the problem by his friend Chevalier de Méré (Antoine Gombaud), an amateur mathematician and a lover of gambling. The question had been publicized many years earlier, among others by the Italian mathematician Luca Pacioli (1446–1517) in a book titled
Everything about Arithmetic, Algebra and Proportions
. The book was published in 1494, more than 150 years before the correspondence between Pascal and Fermat. The mathematical question was given the name the Unfinished Game. We will present here a version of the original question related to tossing a coin. The versions appearing in Pacioli's book and in the Pascal-Fermat correspondence are not significantly more complex. The difficulty in solving the problem was not a computational one but a conceptual one, as we will see. The problem is as follows.
Two players are betting on a hundred-dollar stake. They decide to toss a coin five times. If heads is uppermost in most of the five throws, the first gambler will take the whole amount, and if tails appears more often, then the second one will take the whole amount. They start tossing the coin, but after three times, in which heads has appeared twice and tails once, they cannot continue. The question is, in light of this partial result, how are they to divide the money? To be able to answer the question, we must first define what is meant by “how are they to.” Clearly the issue is not a moral or legal one, such as claiming that as the procedure was stopped, the bet is canceled. From the way the question was formulated by Pacioli and also Pascal and Fermat, it is clear that they are speaking of a fair division based on the outcome until the procedure was stopped.
Given the current understanding of the theory of chance, the answer to the question is simple. The chances of winning must be updated in light of the outcome of the first three tosses of the coin. At the outset, the chances of winning were equal for both players, and if the hundred dollars had been divided before the first toss of the coin each would have received fifty dollars. That would also be the position after two throws, if heads had appeared once and tails once. Calculating the chances in more general cases is not much more complicated. For example, in the situation described in the question, if the coin would have been tossed a fourth time, the chances of heads appearing would be 50 percent, and of tails, 50 percent. If heads appeared, the first gambler would take the whole amount, and if tails came up, then a fifth throw would be needed to decide the outcome. In a fifth throw, again
the chances of heads and tails are equal. Thus, in the fourth throw, only if the outcome was tails (with a 50 percent chance) would a fifth throw be required. So at the fourth throw, with a 2:1 lead, heads has a 50 percent chance of winning the whole game if heads comes up again, and another 25 percent chance if the fourth result is tails and the fifth is heads (i.e., a total of 75 percent), while tails has only a 25 percent chance of winning the game, that is, if the result of both the fourth and fifth throws are tails. So the fair division after the first three throws would give the first player (heads) seventy-five dollars and the second player (tails) twenty-five dollars.
The above analysis uses the concept of chance, a concept that did not exist at the time of Pascal and Fermat. A number of eminent mathematicians addressed this problem before the Pascal-Fermat correspondence, including Cardano, who did not come up with a complete solution, and his rival Tartaglia, who put forward an incorrect solution. The latter also claimed that this was not a mathematical but a legal problem. No agreed solution based on mathematical arguments was reached.
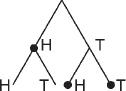
Then, in the first (no longer extant) letter, Pascal described the problem to Fermat and proposed an incorrect solution. The suggestion he put forward was that if the game had continued for the full five throws, there were three possible outcomes, shown by the black circles in the diagram below, which illustrates the fourth and fifth tosses of the coin. Thus, if at the fourth throw heads comes up, then heads has won the game. If tails comes up at the fourth throw and then again at the fifth throw, tails wins the game. Lastly, if tails comes up at the fourth throw, and if heads comes up at the fifth throw, then heads wins. Thus, according to Pascal, because heads has twice as high possibilities of winning the game as tails, the player with heads should get two-thirds of the pool, and tails, one-third. Note that this proposal does not take into account the chances of the different outcomes.
Fermat wrote a reasoned reply, saying that all the possible outcomes of tosses of the coin had to be taken into account, even if the game was decided at the fourth throw, or in today's terminology, the case in which the game was decided by the fourth throw should be given greater weight, of 50 percent. Pascal immediately realized his mistake, and in the brief correspondence that extended over a few months, the fundamental concepts of the theory were developed. Even then the concept of probability did not appear explicitly in their letters, but the essence of the relevant mathematics was presented.
At this stage a few words about Pascal and Fermat are in order. Pierre de Fermat was a lawyer who described himself as an amateur mathematician. He did not depend on mathematics for his livelihood and could therefore choose subjects for research at his leisure. He also did not feel a great need to publish. Only recently was the problem known as Fermat's last theorem solved. The proof was completed in 1995 by Andrew Wiles. It is said that in the margin of one his books Fermat wrote that he has the proof of his theorem but that there was no room to write it in the margin. Even if the story about writing in the margin is true, it is hard to believe that Fermat actually had the proof of his theorem. Number theory was his main field of interest, and he contributed greatly to the subject, but the proof of the theorem requires techniques not available at those times. He also addressed other mathematical questions, for instance, problems related to topics that were eventually developed by Newton and Leibniz into differential and integral calculus, as described in
chapter III
. We also saw in section 21 Fermat's principle that explained the mathematics underlying Snell's law of refraction. All this resulted in Fermat being one of the best-known scientists in Europe at that time.
Pascal, who at the time of the correspondence with Fermat was less known, approached Fermat in respectful deference, and his admiration only grew with his understanding of Fermat's solution to the unfinished-game problem. Pascal very much wanted to meet Fermat, but this never came about. Blaise Pascal's father was a public official, a judge, and a tax collector. The young Pascal helped his father with tax collection and even
invented a mechanical calculator to help with the calculations needed for the job. He made a number of such machines and tried his hand at selling them, a sort of start-up for those days, but did not meet with much success. As a mathematician he showed ability in a variety of subjects but also occupied himself with philosophy and, at a later stage in his short life, became more and more religious, apparently due to an illness he suffered, and stopped dealing with mathematical research. Yet even his theological works had a mathematical feel to them. In one of them he touched on the question of the existence of God, as follows.
Pascal put forward a claim that became known as
Pascal's wager
: We accept, he argued, that there is no ultimate proof of whether God exists or not, but we have to decide whether we believe in his existence or not. We will examine the results of our decision. If God does not exist, the difference between our decision to believe or not believe in his existence would be expressed in only slightly different lifestyles, fulfilling commandments, praying, and so on; that is, a small change only. If on the other hand God does exist, the difference between our decision to believe in his existence or not to believe in it would be enormous. It would mean the difference between eternal life in heaven or perpetual torment in hell. Therefore, just as decisions on how to bet in games of chance, if there is even the smallest chance that God exists, and as stated there is no proof that he does not, the obvious conclusion is that it is worthwhile to believe in the existence of God.
Pascal was interested mainly in the theological aspects of the argument—that indeed were quite novel at the time—yet the analogy with games of chance was in the original text (still without the explicit mention of the concept of probability). This was perhaps the first time that an analysis of a one-time decision, whether to believe in God or not, was made with the help of mathematics and aided by concepts that we call probabilistic concepts. Pascal's analysis became known before it was published in written form in 1670, some seven years after his death.
38. RAPID DEVELOPMENT
The analysis of the unfinished-game problem presented by Fermat and Pascal came just at the time when the need for mathematics that would describe randomness was growing. Possible uses of the concept of randomness led to a growing number of mathematicians involving themselves in the subject, and the theoretical aspects proposed by Fermat and Pascal played a central role in the rapid development of the mathematics of randomness.
There were three main reasons for the increased interest in this area. One, mentioned above, was the spread of gambling and games of chance, with quite a number of scientists and mathematicians among the participants.
The second reason was related to the bankruptcies of many European cities as a result of liabilities for payments of pensions and allowances they had taken upon themselves. Governments and municipalities in Europe, mainly in Holland and England, had for a long time followed the practice of financing their expenditures by taking loans from their citizens, in exchange for which they undertook to pay the lenders fixed amounts as long as they lived. The problem was that the mathematics required to calculate the proper amount of the repayments, and in particular to avoid incurring liabilities that the borrowers would not be able to meet, did not exist at that time. The amount of the regular repayments was determined intuitively or by using calculations that were biased by the borrowers’ desire to raise more and more money. The government of England, for example, issued an ordinance in 1540 that the amount of the annual repayments on a loan had to be such a sum equivalent to the entire amount of the loan that would be repaid in seven years, whereas the annual payments continued until the death of the lender. The age of the lender and the life expectancy of potential lenders was not taken into account. Newton included in his lectures in 1675, and later published in a short paper, a description of how to use the binomial formula to calculate the current value of an interest-bearing account, what is today known as capitalization. He did not even hint at the need for anyone guaranteeing the payments to relate to the average length of life of the recipients
of the payments. The result of this practice was that more and more municipalities went bankrupt. The relevant branch of mathematics, unknown at that time, is of course what the actuarial profession deals with today, namely, calculating the life expectancy of the population of lenders, and hence the expected liability of future payments, and comparing those liabilities with the expected tax revenue. The data required for these calculations, such as mortality tables for different towns, already existed. These had been compiled for years out of curiosity and interest, and especially to understand the effects on mortality rates in different places of the various plagues that struck Europe. The basic concepts of probability and expectation, however, were not known. When municipality after municipality encountered financial difficulties and even bankruptcy, it created pressure to find a solution to the problem, and the development of the mathematics of probability and statistics was given a boost.